
- •1. Введение
- •2. Основные понятия
- •3. Описание лабораторной установки
- •4. Техника безопасности
- •5. Порядок измерений и обработка результатов
- •«Изучение собственных колебаний в электромагнитном контуре»
- •1. Введение
- •2. Основные понятия
- •3. Описание лабораторной установки
- •4. Техника безопасности
- •5. Порядок выполнения работы
- •6. Обработка результатов измерений
- •«Изучение вынужденных колебаний в электромагнитном контуре»
- •1. Введение
- •2. Основные понятия
- •4. Техника безопасности
- •5. Порядок выполнения работы
- •6. Обработка результатов измерений
- •«Изучение собственных колебаний механических систем»
- •1. Введение
- •2. Основные понятия
- •3. Описание лабораторной установки
- •4. Техника безопасности
- •5. Порядок выполнения работы и обработка результатов измерений
- •«Исследование нормальных колебаний струны»
- •1. Введение
- •2. Основные понятия
- •3. Описание лабораторной установки
- •4. Порядок измерений
- •5. Обработка результатов измерений
- •«Определение скорости звука в воздухе»
- •1. Введение
- •2. Основные понятия
- •3. Описание лабораторной установки
- •3.2. Техника безопасности
- •4. Порядок измерений
- •5. Обработка результатов измерений
- •Лабораторная работа № 12-к «изучение интерференции света»
- •1. Введение
- •2. Основные понятия
- •3. Описание лабораторной установки
- •4. Порядок измерений
- •4.1. Заполнить таблицу технических данных (табл. 1).
- •«Дифракция фраунгофера на решетке»
- •1. Введение
- •2. Основные понятия
- •3. Описание установки
- •4. Техника безопасности
- •5. Порядок измерений
Лабораторная работа № 2-К
«ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ФИЗИЧЕСКОГО МАЯТНИКА»
1. Введение
1.1. Среди механических движений важную роль играет колебательное движение, характеризующееся определённой периодичностью. Физическое описание колебаний реального тела – чрезвычайно сложная задача. Поэтому теория колебаний оперирует с моделями: пружинным, математическим, физическим, крутильным маятниками. В основе всех этих моделей лежит представление о линейном гармоническом осцилляторе.
1.2. В классической механике линейный гармонический осциллятор – это материальная точка или абсолютно твёрдое тело, совершающее одномерные гармонические колебания под действием упругой (или квазиупругой) силы.
1.3. В настоящей лабораторной работе изучаются колебания математического и физического маятников и определяются параметры последнего.
2. Основные понятия
2.1. Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена точечная масса. Достаточно хорошим приближением служит небольшой тяжёлый шарик, подвешенный на длинной тонкой нити.
2.2.
Отклонение маятника от положения
равновесия определяется угловым
смещением
 ,
образованным нитью с вертикалью (рис.1).
При этом возникает момент силы тяжестиМ
относительно оси, проходящей через
точку О,
равный по величине M
=
m
g
l
sinφ
( m
–
масса маятника , l
– его длина)
,
образованным нитью с вертикалью (рис.1).
При этом возникает момент силы тяжестиМ
относительно оси, проходящей через
точку О,
равный по величине M
=
m
g
l
sinφ
( m
–
масса маятника , l
– его длина)
Вектор
момента силы имеет такое направление,
что стремится вернуть маятник в положение
равновесия и поэтому при малых
отклонениях, когда
 ,
аналогичен квазиупругой силе. На рис.1
он направлен от нас, перпендикулярно
плоскости чертежа. Применим к
математическому маятнику основное
уравнение динамики вращательного
движения
,
аналогичен квазиупругой силе. На рис.1
он направлен от нас, перпендикулярно
плоскости чертежа. Применим к
математическому маятнику основное
уравнение динамики вращательного
движения ,
гдеJ
–
момент инерции маятника относительно
упомянутой выше оси,
,
гдеJ
–
момент инерции маятника относительно
упомянутой выше оси,
 – угловое ускорение,
– угловое ускорение, - сумма моментов внешних сил. Для проекций
на ось вращения
- сумма моментов внешних сил. Для проекций
на ось вращения
 .
(1)
.
(1)

Рис.1
При
малых углах
 и тогда получаем дифференциальное
уравнение
и тогда получаем дифференциальное
уравнение
 ,
(2)
,
(2)
решением которого являются гармонические колебания
 ,
,
с круговой частотой и периодом соответственно
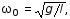
 ,
(3)
,
(3)
которые зависят только от длины l маятника и ускорения свободного
падения g.
2.3. Физическим маятником называется твердое тело, способное совершать колебания вокруг некоторой оси, не проходящей через его центр масс. В положении равновесия центр масс С находится под точкой подвеса О на одной вертикали на расстоянии a (рис.2). При отклонении маятника от положения равновесия возникает момент силы, стремящийся вернуть его обратно.
Так же, как и для математического маятника,
 .
(4)
.
(4)
Здесь J – момент инерции маятника относительно оси, проходящей через точку О. При малых колебаниях уравнение (4) переходит в

 ,
(5)
,
(5)
решением
которого является
 ,
но теперь с круговой частотой
,
но теперь с круговой частотой
 и
периодом
и
периодом
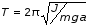 .
(6)
.
(6)

Рис.2
2.4. При сравнении формул (3) и (6) видно, что математический маятник с длиной
 (7)
(7)
будет
иметь такой же период, как и физический.
Величина
 называется приведённой длиной физического
маятника.
называется приведённой длиной физического
маятника.
