
- •Содержание
- •Теоретический раздел « Влияние инфляции на доходы населения» Введение
- •Раздел II. Исследовательский раздел.
- •Раздел II.1. Изучение степени концентрации среднедушевых располагаемых ресурсов населения.
- •Располагаемые ресурсы
- •Валовый доход
- •Денежный доход
- •Стоимость натуральных поступлений продуктов питания
- •Стоимость предоставленных в натуральном выражении дотаций и льгот
- •Сумма привлеченных средств и израсходованных сбережений
- •Раздел II.2. Изучение степени дифференциации населения по величине среднедушевых денежных доходов.
Раздел II.2. Изучение степени дифференциации населения по величине среднедушевых денежных доходов.
Имеются следующие данные о распределении населения России по величине среднедушевых денежных доходов в 2003 году.
Табл. II. 2.1
|
Среднедушевые денежные доходы, руб. в месяц |
Численность населения, млн.чел. |
|
до 2 000 |
34,9 |
|
2 000-3 000 |
34,6 |
|
3 000-4 000 |
29,5 |
|
4 000-5 000 |
18 |
|
5 000- 7500 |
19,8 |
|
7500-120 000 |
6,8 |
|
10 000-15 000 |
2,2 |
|
свыше 15 000 |
1,3 |
Оценить средний размер доходов населения России.
Рассчитать показатели, характеризующие степень дифференциации населения по величине среднедушевых денежных доходов.
Охарактеризовать степень вариации населения по размеру среднедушевых денежных доходов.
Для характеристики среднего размаха дохода населения рассчитывается средняя арифметическая величина.
Для её расчёта используется следующая таблица:
Табл. II.2.2
|
Среднедушевые денежные доходы, руб. в месяц |
Численность населения, млн.чел., fi |
Середина интервала, x’i |
Плотность распределения, mi |
x’i* mi |
Накопленная частота, Fi |
|
до 2 000 |
34,9 |
1500 |
0,0349 |
52,35 |
34,9 |
|
2 000-3 000 |
34,6 |
2500 |
0,0346 |
86,5 |
69,5 |
|
3000-4 000 |
29,5 |
3500 |
0,0295 |
103,25 |
99 |
|
4 000-5 000 |
18 |
4 500 |
0,018 |
81 |
117 |
|
5 000-7 500 |
19,8 |
6000 |
0,0198 |
118,8 |
136,8 |
|
7500-10 000 |
6,8 |
8750 |
0,0068 |
59,5 |
143,6 |
|
10 000-15 000 |
2,2 |
12500 |
0,0022 |
27,5 |
145,8 |
|
свыше 15 000 |
1,3 |
17500 |
0,0013 |
22,75 |
147,1 |
|
ИТОГО: |
147,1 |
|
0,1471 |
551,65 |
|
В гр.3 представлены центральные значения каждого интервала, в гр.4 – плотности распределения населения в каждом интервале.
Середина первого интервала (до 2 000) рассчитывается:
(3 000 – 2 000) / 2 = 500; 2 000 – 500 = 1500.
Середина второго интервала (2 000-3 000) рассчитывается:
(3 000 + 2 000) / 2 = 2500.
Середина последнего интервала (свыше 15 000) рассчитывается:
(15 000 – 10 000) / 2 =2500; 15 000 + 2500 = 17500.
Плотность распределения характеризует численность населения, приходящуюся на единицу длины интервала по доходам, и определяется отношением численности населения к длине интервала. Например, плотность 3-го интервала рассчитывается следующим образом:
m3 = 34,9 / 1 000 = 0,0349
Таким образом, средний доход населения определяется в соответствии с формулой делением итоговых значений гр.5 и 4 табл.II.2.2:

Для оценки степени дифференциации населения по размеру среднедушевых денежных доходов используется децильный коэффициент дифференциации, определяемый как отношение 9-й и 1-й децили в соответствии с формулой:

Номер
1-й децили равен:
 (II.2.1)
(II.2.1)
где n-последняя накопленная частота.
Номер
9-й децили равен:
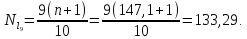 (II.
2.2)
(II.
2.2)
По накопленным частотам гр. 6 табл. II.2.2 определим интервалы, в которых находятся децили.
Первая дециль находится в первом интервале (накопленная частота 36,2).
Девятая дециль – в 5-м интервале (накопленная частота 136,4).
Децили определяются по формуле:
 (
II.
2.3)
(
II.
2.3)
где
 - нижняя граница интервала, в котором
находится дециль;
- нижняя граница интервала, в котором
находится дециль;
 -
номер децили;
-
номер децили;
 -
накопленная частота интервала,
предшествующего тому, в котором находится
дециль;
-
накопленная частота интервала,
предшествующего тому, в котором находится
дециль;
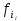 -
частота интервала, в котором находится
дециль;
-
частота интервала, в котором находится
дециль;
i – величина интервала.

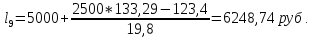
Первая дециль (16 909,39 руб.) характеризует максимальный среднедушевой денежный доход (10%) наименее обеспеченного населения, девятая (82823,08 руб.) – минимальный среднедушевой денежный доход (10%) наиболее обеспеченного населения.
Децильный коэффициент дифференциации определяется по формуле:

Таким образом, минимальный среднедушевой денежный доход (10%) наиболее обеспеченного населения превышает максимальное значение среднедушевого денежного дохода (10%) наименее обеспеченного населения в 4,898 раза.
Оценка степени вариации населения по величине среднедушевых денежных доходов может быть выполнена с использованием показателей вариации: дисперсии, среднего квадратического отклонения, коэффициента вариации.
Поскольку данные представлены в виде ряда распределения, дисперсия определяется следующим образом:
 (II.
2.4)
(II.
2.4)
Для удобства расчета показателей вариации строится следующая вспомогательная таблица:
Табл. II. 2.3
|
Среднедушевые денежные доходы, руб. в месяц |
Численность населения, млн.чел. |
Середина интервала, x’i |
x’i*fi |
(x’i- |
|
до 2 000 |
34,9 |
1 500 |
52350 |
34385046176 |
|
2 000-3 000 |
34,6 |
2 500 |
86500 |
5916547945 |
|
3 000-4 000 |
29,5 |
3 500 |
103250 |
21307283 |
|
4 000-5 000 |
18 |
4 500 |
81000 |
2437417203 |
|
5 000-7 500 |
19,8 |
6 000 |
118800 |
13462306702 |
|
7 500-10 000 |
6,8 |
8 750 |
59500 |
22449552113 |
|
10 000-15 000 |
2,2 |
12 500 |
27500 |
45950338216 |
|
свыше 15 000 |
1,3 |
17 500 |
22750 |
34992010399 |
|
ИТОГО: |
147,1 |
|
551650 |
159589926037 |
Среднее значение признака в совокупности:
 (II.2.5)
(II.2.5)
Отсюда дисперсия будет равна:

Среднее квадратическое отклонение показывает, что денежные доходы населения отклоняются от среднего дохода в среднем на
 (II.
2.6)
(II.
2.6)
Чтобы
судить о величине вариации доходов, эту
величину необходимо сопоставить со
средним доходом, то есть рассчитать
коэффициент вариации. Коэффициент
вариации используется для характеристики
однородности совокупности. Если V то совокупность считается однородной.
то совокупность считается однородной.
 (II.2.7)
(II.2.7)
Величина коэффициента вариации свидетельствует о неоднородности населения РФ по величине среднедушевых денежных доходов.

 )2*fi
)2*fi