6. Синтез исходной замкнутой системы методом корневого годографа.

Корневой годограф -это траектории корней характеристического уравнения (полюсов передаточной функции) замкнутой системы при изменении какого-либо параметра системы.

С помощью функции rlocus() строим корневой годограф по заданной передаточной функции:

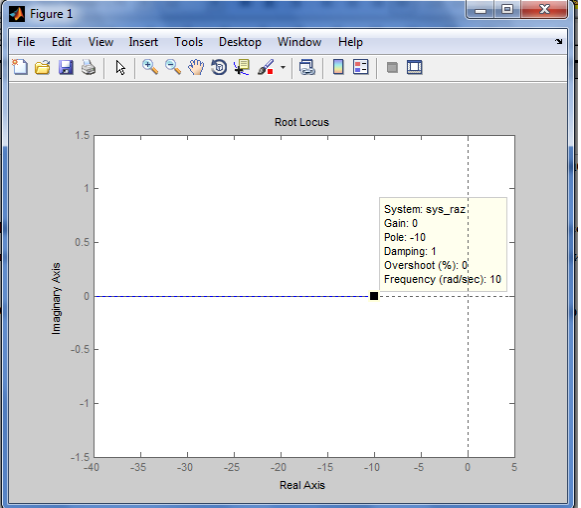
Рис. 10 График корневого годографа

Проанализировав график, можно заключить, что так как график не пересекает ось y, система устойчива на промежутке (0;+∞).

7. Анализ цифровой системы повышенной точности.

Основной чертой цифровых систем является дискретизация.

Дискретизация– представление и использование сигналов в цифровой форме, т.е. квантованными по уровню и времени.

Для выбора периода квантования возможно использовать теорему Котельникова:

T₀ <= 1 / (2*f_max)

digital_sys_raz=c2d(sys_raz,0.1)

Transfer function:

37.93

----------

z - 0.3679

Sampling time: 0.1

digital_sys_zam=feedback(digital_sys_raz,1)

Transfer function:

37.93

---------

z + 37.56

Sampling time: 0.1

step(digital_sys_zam,sys_zam)

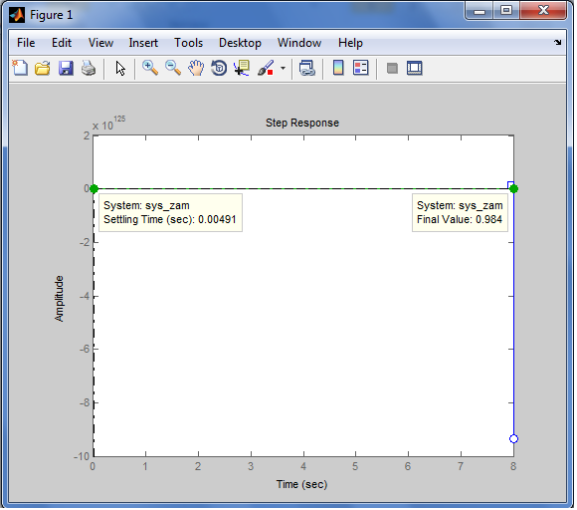
Рис. 11График анализа цифровой системы до и после введения дискретизации

Проанализировав график, делаем вывод, что система не нуждается в дискретизации, так как параметр графиков время переходного процесса (Settling Time)одинаковый.

Заключение:

При исследовании данной системы мной был взят коэффициент k = 20, при котором система достигает наибольшей устойчивости. После проверки первоначальной системы на качество

и устойчивость, я попытался увеличить качество системы варьируя показатели усилителя мощности k. После всех проделанных операций я выяснил, что при увеличенииkкачество системы существенно увеличивается, например приk=200 время переходного процесса значительно улучшилось с 0,00491secдо 0,000498 sec, а погрешность уменьшилась с

0.0164 % до 0.0017%. Это доказывает, что наша система надежна и ее можно применять на практике не только для управления захватом промышленных роботов, но и для других, более точных отраслей производства. По результатам метода корневого годографа можно сделать вывод, что система будет устойчива при 0 < k < +∞ .

Литература

1. Р. Дорф, Р. Бишоп «Современные системы управления», 2002г

2. Энциклопедия «Техника». Росмэн, Москва, 2006г

3. Статьи интернет-энциклопедии Википедия:

http://ru.wikipedia.org/wiki/Робот

http://ru.wikipedia.org/wiki/Промышленный_робот

http://ru.wikipedia.org/wiki/Манипулятор_(механизм)

4. статья “МЕХАНИЗМЫ ЗАХВАТОВ ПРОМЫШЛЕННЫХ РОБОТОВ”

http://futurman.ru/news/2011-03-05-415

5. статья “Конструкции механизмов захватов роботов”

http://www.i-electric.ru/content.html?cid=263

6. статья “Захватные устройства промышленных роботов”

http://hi-robotics.ru/poleznoe/zahvatnie_ustroystva_promishlennih_robotov.html