Свойства энтропии Зависимость энтропии от объема

Рассмотрим, как изменится энтропия одного моля газа при изменении объема системы.

Вместо отношения термодинамических вероятностей подставим соответствующую зависимость (3.7) для 1 моля газа:

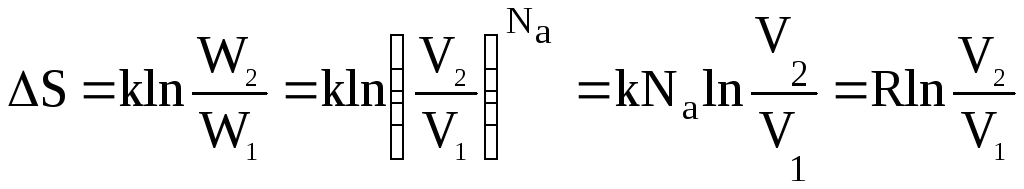(10)

R = 8,31 Дж/мольК, следовательно:

Дж/мольК (11)

Из этого уравнения следует, что процессы, сопровождающиеся увеличением объема системы при сохранении числа молекул, участвующих в процессе, протекают с увеличением энтропии системы.

Зависимость энтропии от давления

Из уравнения состояния идеального газа следует, что для 1 моля газа:

.

Подставляя это выражение в уравнение (3.9), получим для изотермического (протекающего при постоянной температуре) процесса:

(12)

При увеличении давления энтропия системы уменьшается.

Если давление выразить в атмосферах, атмосферное давление обозначить р_о (напомним, что р_о = 1, а энтропию при этом давлении S^o, то получим:

,

или энтропия при давлении p равна:

.

(13)

Следует обратить внимание, что в уравнении (13) р выражено в абсолютных атмосферах. Если в условиях задачи давление дается в атмосферах избыточных, необходимо перевести его в абсолютные:

р_абс. = р_изб. +1.

Полученная зависимость (13) характерна только для газовой фазы, на энтропию конденсированных (твердых, жидких) систем изменение давления практически не оказывает влияние, а влияют такие факторы, как тип кристаллической решетки, прочность связей и т.д.

Так, величины энтропии твердого фосфора значительно различаются в зависимости от типа кристаллической решетки («белая» или «красная» модификация):

S^о_{298,Р(бел)} = 41,09 Дж/моль·К; S^о_298,Р(кр) = 22,8 Дж/моль·К.

Зависимость энтропии от температуры

С повышением температуры энтропия возрастает.

Действительно температура повышается за счет подвода теплоты (по мерее увеличения температуры становится возможным все большее число состояний, так как молекулы могут переходить в состояние со все более высокими значениями энергии, что приводит к увеличению термодинамической вероятности), При постоянном давлении и небольшом изменении температуры (С_Р принимается постоянной) изменение энтропии системы можно выразить как, (см. уравнение 8):

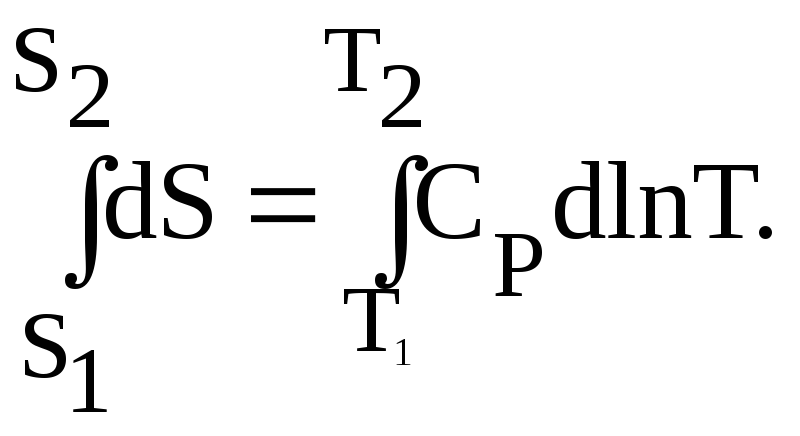(14)

Интегрируя это уравнение, получаем следующее выражение:

(14а)

На рис. 4. показан характер зависимости энтропии вещества от температуры. Как видно из рисунка 4, при фазовом переходе (ф.п.) вещества (из твердого состояния в жидкое, из жидкого в газообразное состояние) энтропия вещества скачкообразно возрастает, что связано с переходом в состояние с большей неупорядоченностью.

Изменение энтропии вещества при любых фазовых переходах (ф.п.) равно:

.

(15)

Зависимость энтропии вещества от температуры при постоянстве фазового состава определяется уравнением (14а).

В интервале умеренных температур (300 - 500К) этим изменением при ориентировочных расчетах часто пренебрегают.

Уравнение температурной зависимости энтропии 1 моля вещества в пределах одного фазового состояния:

, (16)

где С_р – мольная теплоемкость при р = const.

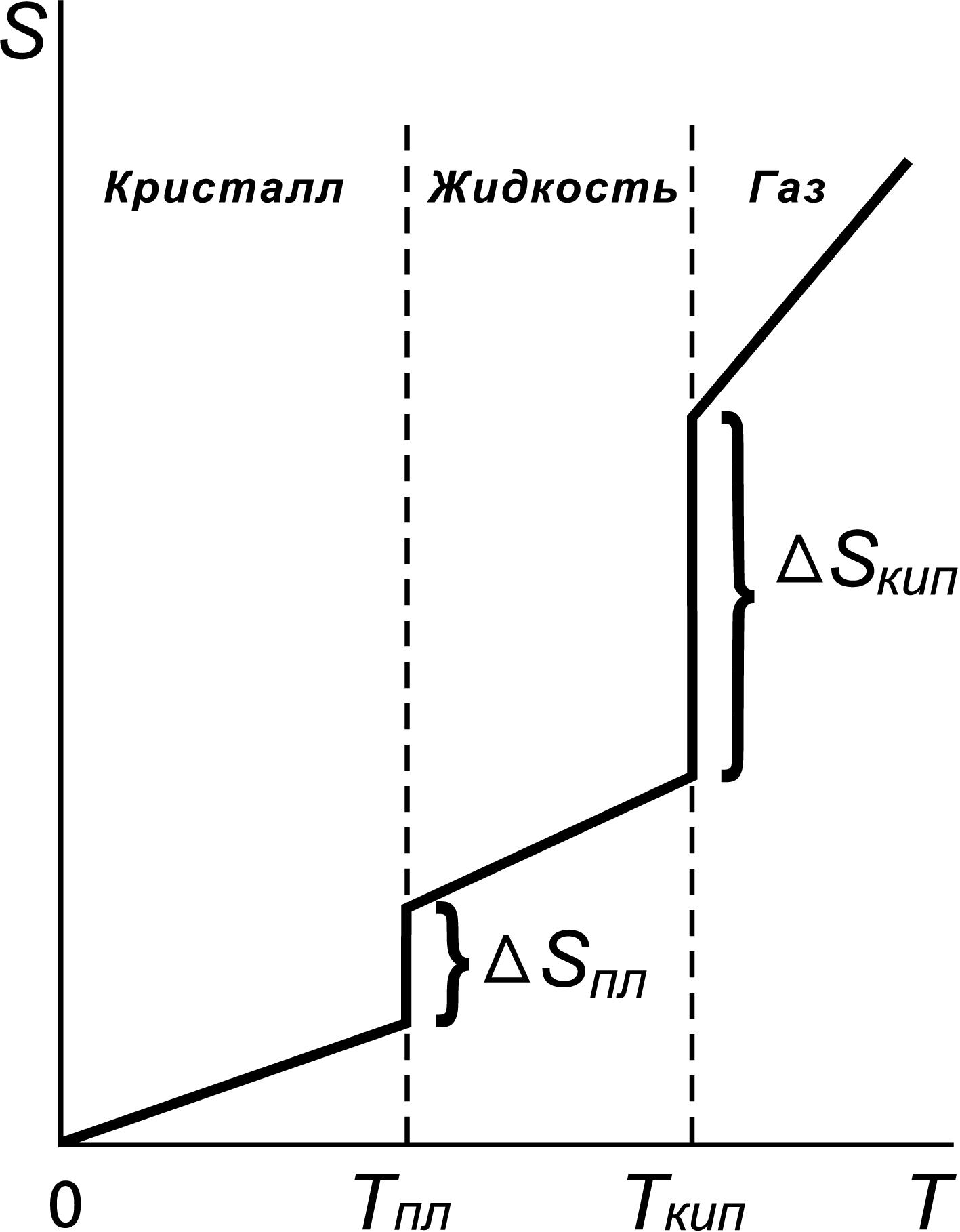
Рис. 4. Зависимость энтропии вещества от температуры.

Принимая С_р = const в интервале температур Т₁ и Т₂ получаем

. (17)

Обратите внимание, что зависимость на рис.4 выходит из начала координат. При температуре равной абсолютному нулю тепловое движение отсутствует, все атомы в идеальном кристалле занимают строго определенные места в пространстве. Такое состояние системы может быть реализовано единственным способом, поэтому при этом W = 1, а S = 0. Это третий закон термодинамики, называемый также постулатом Планка.
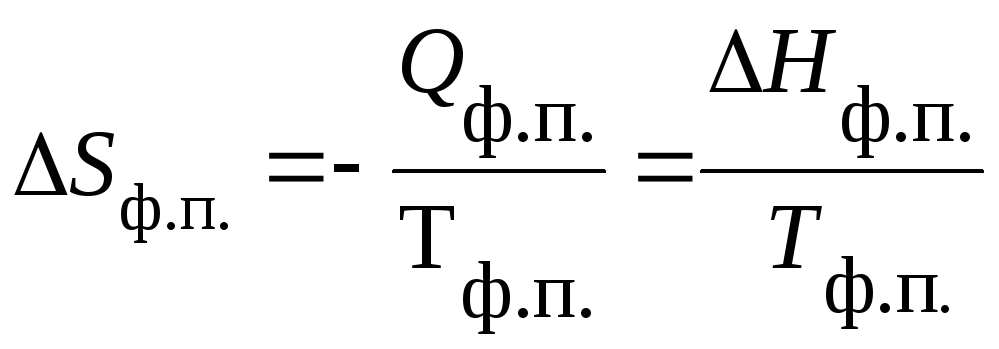