Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский автомобильно-дорожный государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

statist4 - копия 1.doc

Скачиваний:

Добавлен:

15.05.2015

Размер:

932.35 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Раздел V. Корелляционая связь и её статистической изучение.

У- производительность труда (выпуск товаров и услуг на одного рабочего.

X– уровень вооруженности труда ОПФ (стоимость ОПФ на одного рабочего).

№ предприятия	Выпуск товаров и услуг в марте, тыс.р.	Среднемесячная стоимость ОПФ в марте	Среднесписочная численность работников в марте, чел.	Среднемесячная стоимость ОПФ в марте на одного работника (х)	Выпуск товаров и услуг в марте на одного работника, тыс.р. (у)
32	1905	808	100	8,080	19,050
33	1400	544	96	5,667	14,583
34	1802	632	98	6,449	18,388
35	1411	457	85	5,376	16,600
36	593	232	78	2,974	7,603
37	1597	536	92	5,826	17,359
38	813	296	77	3,844	10,558
39	1417	453	84	5,393	16,869
40	1708	712	104	6,846	16,423
41	1317	649	81	8,012	16,259
50	808	672	74	9,081	10,919
51	613	448	82	5,463	7,476
52	1562	785	97	8,093	16,103
53	1286	672	74	9,081	17,378
54	1178	800	76	10,526	15,500
55	1705	859	96	8,948	17,760
56	1935	1020	113	9,027	17,124
57	1800	999	108	9,250	16,667
58	1598	845	105	8,048	15,219
59	1880	894	114	7,842	16,491
60	1519	754	98	7,694	15,500
61	832	596	77	7,740	10,805
62	1690	989	98	10,092	17,245
63	1190	672	84	8,000	14,167
64	500	395	66	5,985	7,576
65	1812	942	108	8,722	16,778
66	1410	754	95	7,937	14,842
67	1720	939	94	9,989	18,298
68	1735	981	100	9,810	17,350
69	1920	1035	112	9,241	17,143

Берём 6 групп по Хi и 6 групп по Уi

Корреляционная Таблица.

Интервалы x_i	Интервалы y_i						Число наблюдений mi	Среднее значение в данном интервале по Xi
	7,476-9,405	9,405-11,334	11,334-13,263	13,263-15,192	15,192-17,121	17,121-19,05

2,974-4,233	7,603	10,558					2	9,081

4,233-5,492	7,476				16,600		3	13,648
					16,869
5,492-6,751	7,576			14,583		18,388	4	14,476
						17,359
6,751-8,01		10,805		14,842	16,491		6	14,705
					15,500
				14,167	16,423
8,01-9,269		10,919			16,778	19,050	11	16,400
					15,219	17,760
					16,103	17,378
					16,259	17,124
					16,667	17,143
9,269-10,528					15,500	18,298	4	17,098
						17,245
						17,350
Число наблюдений	3	3	0	3	11	10	30

Х1=3,604 Y1=9,081 Х2=4,863Y2=13,648

Х3=6,122 Y3=14,476

Х4=7,381 Y4=14,705 Х5=8,64Y5=16,400

Х6=9,9 Y6=17,098

Вспомогательная таблица для расчёта сумм слагаемых в системе уравнений.

№ n/n	x_i	y_i	x_i²	y_i²	y_i*x_i
1	2,974	7,603	8,847	57,799	22,613	10,691
2	3,844	10,558	14,778	111,481	40,588	11,520
3	5,376	16,600	28,906	275,560	89,249	12,981
4	5,393	16,869	29,083	284,565	90,972	12,997
5	5,463	7,476	29,849	55,885	40,842	13,064
6	5,667	14,583	32,111	212,674	82,639	13,258
7	5,826	17,359	33,943	301,324	101,133	13,410
8	5,985	7,576	35,818	57,392	45,340	13,561
9	6,449	18,388	41,589	338,110	118,582	14,004
10	6,846	16,423	46,870	269,717	112,435	14,383
11	7,694	15,500	59,196	240,250	119,255	15,191
12	7,740	10,805	59,912	116,752	83,635	15,235
13	7,842	16,491	61,499	271,961	129,326	15,332
14	7,937	14,842	62,993	220,288	117,799	15,423
15	8,000	14,167	64,000	200,694	113,333	15,483
16	8,012	16,259	64,198	264,364	130,275	15,495
17	8,048	15,219	64,764	231,619	122,477	15,528
18	8,080	19,050	65,286	362,903	153,924	15,559
19	8,093	16,103	65,493	259,310	130,319	15,571
20	8,722	16,778	76,077	281,494	146,340	16,172
21	8,948	17,760	80,065	315,432	158,919	16,387
22	9,027	17,124	81,479	293,228	154,570	16,462
23	9,081	10,919	82,466	119,223	99,156	16,514
24	9,081	17,378	82,466	302,008	157,814	16,514
25	9,241	17,143	85,397	293,878	158,418	16,666
26	9,250	16,667	85,563	277,778	154,167	16,675
27	9,810	17,350	96,236	301,023	170,204	17,209
28	9,989	18,298	99,787	334,812	182,784	17,380
29	10,092	17,245	101,845	297,387	174,033	17,478
30	10,526	15,500	110,803	240,250	163,158	17,892
	229,037	454,033	1851,320	7189,158	3564,299	454,033

Линейная зависимость:.

Система «нормальных» уравнений имеет вид:

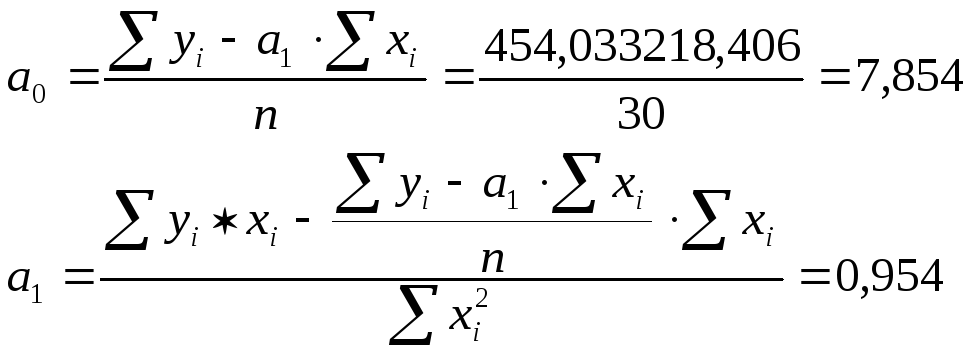
x_i	m_i	x_i*m_i			у_i	m_i	у_i*m_i
2,974	1	2,974	4,660	21,718	7,476	1	7,476	7,659	58,657
3,844	1	3,844	3,790	14,367	7,576	1	7,576	7,559	57,133
5,376	1	5,376	2,258	5,099	7,603	1	7,603	7,532	56,729
5,393	1	5,393	2,242	5,025	10,558	1	10,558	4,576	20,940
5,463	1	5,463	2,171	4,714	10,805	1	10,805	4,329	18,742
5,667	1	5,667	1,968	3,873	10,919	1	10,919	4,215	17,770
5,826	1	5,826	1,808	3,271	14,167	1	14,167	0,968	0,937
5,985	1	5,985	1,650	2,722	14,583	1	14,583	0,551	0,304
6,449	1	6,449	1,186	1,406	14,842	1	14,842	0,292	0,085
6,846	1	6,846	0,788	0,622	15,219	1	15,219	0,085	0,007
7,694	1	7,694	0,059	0,004	15,500	2	31,000	0,366	0,267
7,740	1	7,740	0,106	0,011	16,103	1	16,103	0,969	0,938
7,842	1	7,842	0,208	0,043	16,259	1	16,259	1,125	1,265
7,937	1	7,937	0,302	0,091	16,423	1	16,423	1,289	1,661
8,000	1	8,000	0,365	0,134	16,491	1	16,491	1,357	1,841
8,012	1	8,012	0,378	0,143	16,600	1	16,600	1,466	2,148
8,048	1	8,048	0,413	0,171	16,667	1	16,667	1,532	2,348
8,080	1	8,080	0,445	0,198	16,778	1	16,778	1,643	2,701
8,093	1	8,093	0,458	0,210	16,869	1	16,869	1,735	3,009
8,722	1	8,722	1,088	1,183	17,124	1	17,124	1,989	3,958
8,948	1	8,948	1,313	1,725	17,143	1	17,143	2,008	4,034
9,027	1	9,027	1,392	1,938	17,245	1	17,245	2,110	4,454
9,081	2	18,162	1,447	4,185	17,350	1	17,350	2,216	4,909
9,241	1	9,241	1,606	2,581	17,359	1	17,359	2,224	4,947
9,250	1	9,250	1,615	2,610	17,378	1	17,378	2,244	5,035
9,810	1	9,810	2,175	4,732	17,760	1	17,760	2,626	6,896
9,989	1	9,989	2,355	5,545	18,298	1	18,298	3,163	10,007
10,092	1	10,092	2,457	6,038	18,388	1	18,388	3,253	10,584
10,526	1	10,526	2,892	8,362	19,050	1	19,050	3,916	15,332
	30	229,037		102,718		30	454,033		317,639

Линейные коэффициент корреляций:

Оценка значимости линейного коэффициента корреляций осуществуется по формуле:

Kоэффициент корреляций

где - дисперсия фактораY;

- дисперсияYпод действием всех факторов, кроме Х:

где - фактическое значение фактораY;

- выравнивание по Х значения результативного показателя;

- показывает относительное значение вариации под действие фактора Х в общей вариации

=10,588

у_i
7,476	13,064	31,231
7,576	13,561	35,827
7,603	10,691	9,536
10,558	11,520	0,925
10,805	15,235	19,625
10,919	16,514	31,303
14,167	15,483	1,732
14,583	13,258	1,757
14,842	15,423	0,337
15,219	15,528	0,096
15,500	15,191	0,095
15,500	17,892	5,721
16,103	15,571	0,283
16,259	15,495	0,585
16,423	14,383	4,163
16,491	15,332	1,343
16,600	12,981	13,096
16,667	16,675	0,000
16,778	16,172	0,367
16,869	12,997	14,994
17,124	16,462	0,438
17,143	16,666	0,227
17,245	17,478	0,054
17,350	17,209	0,020
17,359	13,410	15,593
17,378	16,514	0,747
17,760	16,387	1,887
18,298	17,380	0,843
18,388	14,004	19,218
19,050	15,559	12,186
		224,230

В качестве меры достоверности уравнения корреляционной зависимости используется процентное отношение средней квадратической ошибки уравнения (S) к среднему уровню результативного признака ():

где - фактические значения результативного признака;

-значения результативного признака, рассчитанные по уравнению регрессии;

l– число параметров в уравнении регрессии.

Вывод:

По корреляционной таблице можно предположить, что связь прямая.

Чем ближе величина rк единице, тем теснее взаимосвязь междуXиY. Следовательно, из полученных данных (r=0,542,R=0,542) видно, что зависимость между стоимостью ОПФ на одного работника и выпуском товаров и услуг на работника не является тесной. Она средняя.

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.05.2015224.96 Кб33sotsiologia_1.docx
#
01.03.202589.78 Кб0sotsiologia_ekz.docx
#
01.04.2025161.28 Кб0sots_otvety_1.doc
#
01.04.2025412.67 Кб0SPORY.doc
#
01.04.2025949.25 Кб0stat.doc
#
15.05.2015932.35 Кб29statist4 - копия 1.doc
#
14.09.20191.47 Mб29stat_doc_sonya.doc
#
15.05.2015228.92 Кб48stroitelnoe_materialovedenie.docx
#
15.05.20154.16 Mб194stroitelstvo_v_vide_shpor.docx
#
01.05.20251.53 Mб2Struktur_777.doc
#
01.03.2025970.43 Кб6StudentBank.ru_15165.rtf