4. Производные высших порядков. Механический смысл второй производной.

Рассмотрим дифференцируемую функцию . Найдем её производную . Рассматривая  как новую функцию, продифференцируем её:

Полученную новую производную называют второй производной от функции . Вторую производную обозначают так:

 или .

Аналогично находится производная третьего, четвертого, и т.д. n-го порядка. Третья производная обозначается так:

Четвертая:

.

Производной n – го порядка от функции  называется производная от производной -го порядка:

.

Производные высших порядков вычисляются последовательным дифференцированием данной функции.

Механический смысл второй производной:

Если точка движется прямолинейно и задан закон ее движения , то ускорение точки равно второй производной от пути по времени:

4. Дифференцирование функций, заданных параметрически (первая и вторая производные).

Пусть функции x = (t) и y = ψ(t) определены на некотором отрезке [α, β]. Переменную t будем называть параметром.

Если x = (t) взаимно однозначна на отрезке [α, β], то она имеет обратную функцию t(x) =  ^{− 1} (x). Подставляя ее в равенство y = ψ(t), видим, что переменная y является сложной функцией переменной x: y   =   ψ( ^{− 1} (x) )   ≡   f(x)

 В этом случае говорят, что функция y = f(x) задана параметрически уравнениями 

   x = (t) y = ψ(t)

где t  [α, β].

Производная первого порядка функции, заданной параметрически

Теорема 1. Пусть функция y = f(x) задана параметрически уравнениями (1), причем функции (t) и ψ(t) дифференцируемы в некоторой точке t₀ (α, β), и  '(t₀) ≠ 0.

Тогда функция y = f(x) дифференцируема в точке x₀ = (t₀), причем

 

Доказательство. В условиях теоремы функция (t) имеет дифференцируемую обратную функцию t(x) =  ^{− 1} (x), производная которой в точке x₀ = (t₀)определяется формулой

.

 Дифференцируя f(x) = ψ(t(x)) в точке x₀ = (t₀) как сложную функцию x, при t = t₀ получаем 

 

Производная второго порядка функции, заданной параметрически

Если функции (t) и ψ(t) дважды дифференцируемы в некоторой точке t₀  (α, β) и  '(t₀) ≠ 0, то

 

4. Теоремы о дифференцируемых функциях (Ферма, Ролля, Лагранжа).

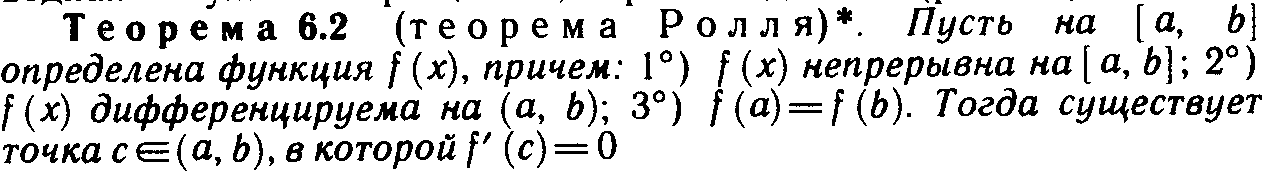
4. Правило Лопиталя раскрытия неопределенностей.

4. Исследование функции на монотонность с помощью производной.

Если производная функции  на некотором промежутке , то функция  возрастает на этом промежутке; если же  на промежутке , то функция  убывает на этом промежутке. Если функция возрастает на промежутке, то или не существует.

4. Исследование функции на экстремум с помощью производной. Необходимые и достаточные условия экстремума.

Пусть функция f (х) имеет в точке  и ее окрестности  непрерывные первую и вторую производные, причем .  

Тогда функция f (х)  достигает в точке  минимума (максимума), если  (соответственно ).  Эта теорема позволяет сформулировать  правило исследования функции на экстремум с помощью второй производной. По сравнению с предыдущим правилом меняется лишь п. 3, который заменяется на следующий: находят вторую производную f " (х), вычисляют ее  значения для каждого из корней уравнения f ′ (х) = 0 и согласно теореме делают заключение об экстремуме.  Заметим, что пользоваться вторым правилом обычно проще, чем первым. Однако если вторая производная при значении, равном корню  первой производной, обращается в нуль, то  используют первое правило отыскания экстремума.