Следствия

1. Условие компланарности векторов: три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.

2. ([→a, →b ], →c ) = (→a, [→b, →c ]);

3. (→a, →b, →c) = (→b, →c, →a) = (→c, →a, →b);

4. (→a, →b, →c) = − (→b, →a, →c).

4. Уравнения прямой на плоскости (общее; каноническое; с заданными угловым коэффициентом и точкой; угловым коэффициентом и отрезком, отсекаемым на оси ординат; по двум данным точкам, "в отрезках").

Теорема.

Всякое уравнение первой степени с двумя переменными x и y вида , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая прямая на плоскости задается уравнением вида .

Уравнение  называется общим уравнением прямой на плоскости.

Общее уравнение прямой называется полным, если все числа А, В и С отличны от нуля, в противном случае общее уравнение прямой называется неполным. Неполное уравнение прямой вида  определяют прямую, проходящую через начало координат. При А=0уравнение  задает прямую, параллельную оси абсцисс Ox, а при В=0 – параллельную оси ординат Oy.

ормальный вектор прямой, заданной общим уравнением прямой вида , имеет координаты .

Уравнение прямой вида , где a и b – некоторые действительные числа отличные от нуля, называется уравнением прямой в отрезках. 

Уравнение прямой вида , где x и y - переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой коэффициент). 

Определение углового коэффициента прямой дается через определение угла наклона прямой к положительному направлению оси Ox.

Определение.

Углом наклона прямой к положительному направлению оси абсцисс в данной прямоугольной декартовой системе координат Oxy называют угол , отсчитываемый от положительного направления оси Ох до данной прямой против хода часовой стрелки.

Если прямая параллельна оси абсцисс или совпадает с ней, то угол ее наклона считают равным нулю.

Определение.

Угловой коэффициент прямой есть тангенс угла наклона этой прямой, то есть, .

Каноническое уравнение прямой на плоскости в прямоугольной декартовой системе координат Oxy имеет вид , где  и  – некоторые действительные числа, причем  и  одновременно не равны нулю.

Очевидно, что прямая линия, определяемая каноническим уравнением прямой, проходит через точку . В свою очередь числа  и , стоящие в знаменателях дробей, представляют собой координаты направляющего вектора этой прямой. Таким образом, каноническое уравнение прямой 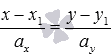 в прямоугольной системе координат Oxy на плоскости соответствует прямой, проходящей через точку  и имеющей направляющий вектор .

4. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности прямых.

?????

4. Уравнения плоскости в простанстве (общее; через данную точку перпендикулярно вектору нормали, через данную точку параллельно направляющим векторам, через три данные точки).

Всякое уравнение первой степени относительно координат x, y, z

Ax + By + Cz +D = 0                                        (3.1)

задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.

Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.

Особые случаи уравнения (3.1):

1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: x = 0, y = 0, z = 0.

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A₁ x + B₁ y + C₁ z + D₁ = 0, A₂ x + B₂ y + C₂ z + D₂ = 0;              (3.2)

2) двумя своими точками M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), тогда прямая, через них проходящая, задается уравнениями:

=;                                       (3.3)

3) точкой M₁(x₁, y₁, z₁), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

.                                        (3.4)

Уравнения (3.4) называются каноническими уравнениями прямой.

Вектор a называется направляющим вектором прямой.

Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:

x = x₁ +mt, y = y₁ + nt, z = z₁ + рt.                              (3.5)

Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой:

x = mz + a, y = nz + b.                                      (3.6)

От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:

.

От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [n₁, n₂], где n₁(A₁, B₁, C₁) и n₂(A₂, B₂, C₂) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система

равносильна системе ; такая прямая перпендикулярна к оси Ох.

Система  равносильна системе x = x₁, y = y₁; прямая параллельна оси Oz.

4. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей. Расстояние от точки до плоскости.

4. Прямая в пространстве. Уравнения прямой в пространстве (общие; канонические; через две данные точки).

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Прямую в пространстве невозможно задать одним уравнением. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой. Для этого требуется система двух или более уравнений.

Пусть две плоскости  и  заданы общими уравнениями вида  и , т.к. коэффициенты  и  не пропорциональны, то плоскости не параллельные. Тогда прямая в пространстве есть пересечение этих плоскостей:

 

 

Эти уравнения называются общими уравнениями прямой.