
Контр. работа 2011
.doc
Итоговая контрольная работа
Вариант 1
Тема 1. Элементы теории множеств
Задача 1
Приведите определение термина «область определения функции» в терминах теории множеств
Н![]() айдите
область определения функции. Покажите
результат аналитически и на числовой
оси
айдите
область определения функции. Покажите
результат аналитически и на числовой
оси
Задача 2
Дайте определение термина «числовая последовательность» с точки зрения теории множеств.
Д![]() ана
числовая последовательность, n-й
элемент которой равен
ана
числовая последовательность, n-й
элемент которой равен
Напишите первые семь
элементов числовой последовательности.
Приведите точечный график элементов
последовательности. Оцените предел
последовательности при
 .
.
Тема 2. Прогрессии. Проценты
Задача 1
Найдите разность, первые шесть членов арифметической прогрессии, заданной двумя членами: a2 = 12,
a10 = -4. Постройте точечный график первых шести членов прогрессии. Как изменяется n-ный член прогрессии с увеличением n?
Задача 2
Найдите четвертый член и сумму пяти первых членов геометрической прогрессии, заданной ее членами:
b2 = 6, b5 = 162. Как изменяется n-й член прогрессии с увеличением n?
Задача 3
Земельный участок имеет форму квадрата. Оцените ( в процентах) изменение площади участка, если :
а) одна из сторон увеличится на 20%; б) обе стороны уменьшатся на 10%
Задача 4
При уплате в Сбербанке штрафа по квитанции ГИБДД автолюбителю за просрочку начислили пеню в размере 6%. Каков был размер штрафа, если всего пришлось заплатить 84 руб. 80 коп.?
Задача 5
Вкладчик вложил в Сбербанк сумму в размере 7000 $ при годовой процентной ставке р% =10%
Вкладчику было предложено выбрать одну из трех схем начисления процентов:
-
Схему простых процентов;
-
Схему сложных процентов с ежегодным начислением процентов
-
Схему сложных процентов с ежемесячным начислением процентов
Какую сумму может получить вкладчик по каждой из предложенных схем: а) через шесть месяцев; б)через год; в) через полтора года .
Приведите необходимые расчетные формулы, результаты вычислений. Сделайте вывод о целесообразности применения каждой из схем.
Тема 3. Основы математического анализа
Задача 1
Н![]()
![]()
![]()
![]() айдите
пределы выражений:
айдите
пределы выражений:
Задача 2
Пользуясь таблицей формул дифференцирования, найдите первую производную функции.
![]()
Какие методы дифференцирования Вы использовали
Задача 3
Что такое дифференциал функции? Каков его геометрический смысл?
Найдите дифференциал функции:
![]()
Покажите последовательность действий, необходимых для вычисления дифференциала
Задача 4
Н![]()
![]()
![]() айдите
следующие неопределенные интегралы.
Объясните, по какому методу вычислялся
каждый интеграл
айдите
следующие неопределенные интегралы.
Объясните, по какому методу вычислялся
каждый интеграл
Задача 5
О пределенный
интеграл – дайте определение. Вычислите
определенный интеграл. Приведите метод
вычисления.
пределенный
интеграл – дайте определение. Вычислите
определенный интеграл. Приведите метод
вычисления.
Задача 6
В![]() ычислите
площадь, ограниченную параболой,
ычислите
площадь, ограниченную параболой,
прямыми x = -1 и x = 2 и осью абсцисс. Приведите график функции, заштрихуйте вычисляемую площадь
Задача 7
![]() Дана
функция
Дана
функция
Найдите:
-
Область определения функции.
-
Точки разрыва и вертикальные асимптоты. Определите интервалы непрерывности.
-
Исследуйте функцию на четность, нечетность, периодичность.
-
Пределы функции на границах области определения
 .
Совместите с определением наклонных
асимптот
.
Совместите с определением наклонных
асимптот -
Первую производную, точки экстремумов и интервалы монотонности.
-
Вторую производную, точки перегиба и характер выпуклости.
-
Точки пересечения функции с осями координат OX и оy (если это возможно).
-
Постройте график функции.
-
Вычислите площадь S криволинейной трапеции, ограниченной графиком функции, осью OX и прямыми x = 0 и x = 2.
Ответы на основные вопросы:
-
минимум функции ymin(0) = 2; максимум функции ymax(-4) = -6
-
точек перегиба нет
-
вертикальная асимптота x = -2;
-
наклонная асимптота y = x;
-
площадь S = 2 + 4ln3 .
Вариант 2
Тема 1. Теория множеств
Задача 1
Приведите определение термина «область определения функции» в терминах теории множеств
Н![]() айдите
область определения функции. Покажите
результат аналитически и на числовой
оси.
айдите
область определения функции. Покажите
результат аналитически и на числовой
оси.
Задача 2
Дайте определение термина «числовая последовательность» с точки зрения теории множеств
Д![]() ана
числовая последовательность, n-й
элемент которой равен
ана
числовая последовательность, n-й
элемент которой равен
Напишите первые пять элементов последовательности. Приведите точечный график последовательности.
Оцените предел
последовательности при
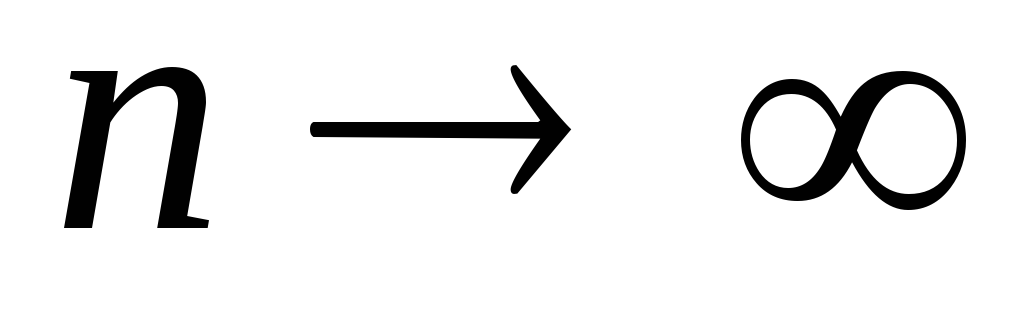
Тема 2. Прогрессии. Проценты
Задача 1
Найдите разность, первые шесть членов арифметической прогрессии, заданной двумя членами:a4 = 8, a10 = 2. Постройте точечный график первых шести членов прогрессию Как изменяется n-ный член прогрессии с увеличением n?
Задача 2
Найдите пятый член и сумму пяти первых членов геометрической прогрессии, заданной ее членами: b3 = 96, b6 = 12. Как изменяется n-й член прогрессии с увеличением n?
Задача 3
Земельный участок имеет форму прямоугольника со сторонами а и 2а. Как изменится (в процентах) периметр участка, если: а) каждая из сторон увеличится на 10%; б) каждая из сторон уменьшится вдвое.
Задача 4
В январе завод выполнил 104% месячного плана выпуска продукции, а в феврале дал продукции на 5% больше, чем в январе. На сколько процентов завод перевыполнил а) двухмесячный план выпуска продукции; среднемесячный план выпуска продукции.
Задача 5
Вкладчик вложил в банк СБ сумму в размере 100000 руб. при годовой процентной ставке р%=30%.
Вкладчику было предложено выбрать одну из трех схем начисления процентов:
-
Схему простых процентов;
-
Схему сложных процентов с ежегодным начислением процентов
-
Схему сложных процентов с ежемесячным начислением процентов
Какую сумму может получить вкладчик по каждой из предложенных схем: а) через восемь месяцев; б) через год; в) через год и шесть месяцев года .
Приведите необходимые расчетные формулы, результаты вычислений. Сделайте вывод о целесообразности применения каждой из схем.
Тема 3. Основы математического анализа
Задача 1
Н![]()
![]()
![]()
![]() айдите
пределы выражений
айдите
пределы выражений
Задача 2
П![]() ользуясь
таблицей формул дифференцирования,
найдите первую производную функции
ользуясь
таблицей формул дифференцирования,
найдите первую производную функции
Какие методы дифференцирования Вы использовали.
Задача 3
Н![]() айдите
дифференциал функции:
айдите
дифференциал функции:
Ответьте на вопросы: дифференциал - аналитический и геометрический смысл; последовательность действий, необходимых для вычисления дифференциала.
 Задача
4
Задача
4
Н![]()
![]()
![]() айдите
следующие неопределенные интегралы.
Объясните, по какому методу вычислялся
каждый интеграл
айдите
следующие неопределенные интегралы.
Объясните, по какому методу вычислялся
каждый интеграл
З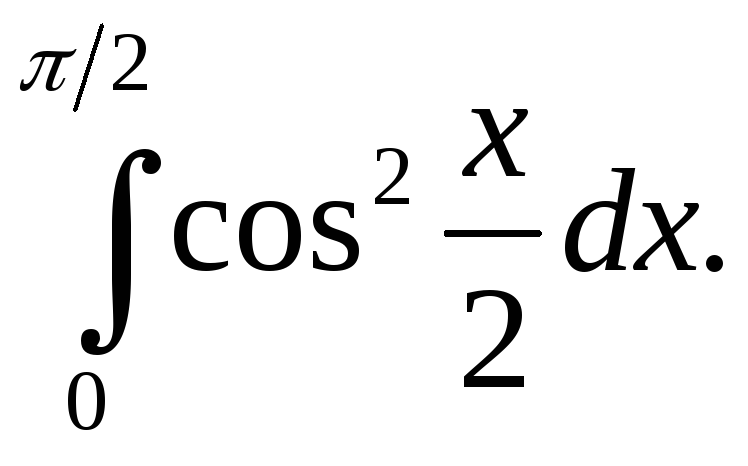 адача
5. Определенный интеграл – дайте
определение. Вычислите определенный
интеграл
адача
5. Определенный интеграл – дайте
определение. Вычислите определенный
интеграл
Примечание:
![]()
Задача 6
В![]() ычислите
площадь, ограниченную параболой
ычислите
площадь, ограниченную параболой
прямой y1 = -2 и прямыми х=-1 и х=1. Приведите графики функций y и y1, заштрихуйте вычисляемую площадь.
Задача 7
![]() Дана
функция
Дана
функция
Найдите:
-
Область определения функции.
-
Точки пересечения функции с осью OX (если это возможно).
-
Исследуйте функцию на четность, нечетность, периодичность.
-
Точки разрыва.
-
Вертикальные и наклонные асимптоты.
-
Интервалы монотонности.
-
Точки экстремумов.
-
Точки перегиба и характер выпуклости.
-
Постройте график функции.
-
Вычислите площадь S криволинейной трапеции, ограниченной графиком функции, осью OX и прямыми x = 0 и x = 1.
Ответы на основные вопросы:
-
минимум функции ymin(0) = 0;
-
максимум функции ymax(-2) = -4;
-
точки перегиба: нет
-
наклонная асимптота y =x-1;
-
площадь S = ln2 -1/2.
