6.2. Гистограммы

При анализе итогов описательной статистики возникли сомнения относительно вида распределений запросов. Чтобы развеять или подтвердить их, построим гистограммы значений запросов.

Рассматривая графики гистограмм можно убедиться, что предположения о ненормальности распределений, сделанные по результатам анализа описательной статистики, подтверждаются. Действительно, гистограмма запросов земли (рис. 2) может восприниматься как плоская и более или менее симметричная. Кроме того, имеются два выраженных максимума.

Гистограмма запросов ОКС (рис. 3) асимметричная.

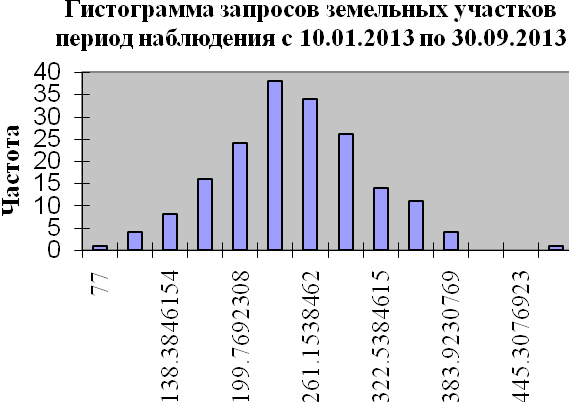
Рис. 2

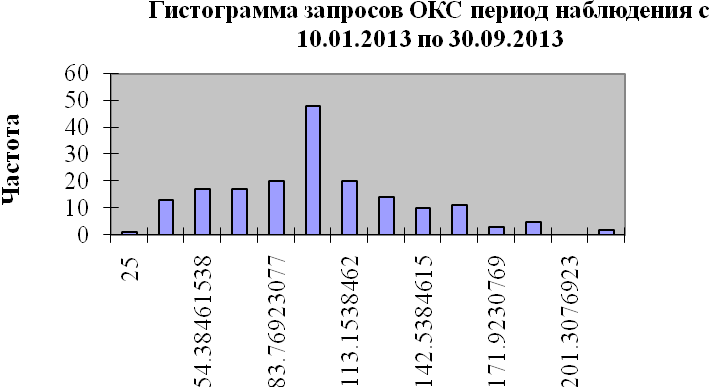
Рис. 3

Итак, в результате анализа итогов описательной статистики и гистограмм можно с уверенностью сказать, что количество запросов распределены по законам, отличающимся от нормального. Этот факт нужно учитывать при последующем анализе.

6.3. Корреляция динамических рядов количества запросов

Один из способов обнаружения тренда (тенденции) динамического ряда состоит в вычислении коэффициентов корреляции ряда. При этом оценивается сила линейной зависимости уровней ряда от времени.

Значения выборочных коэффициентов корреляции рассчитаны с помощью стандартной функции Excel. Они равны:

- для запросов земли он равен -0.12;

- для запросов ОКС равен 0.60.

Коэффициент корреляции количества запросов земельных участков отрицательный. Это означает, что с течением времени запросы по земельным участкам в среднем падают.

Коэффициент корреляции количества запросов по ОКС положительный. Это означает, что с течением времени запросы по ОКС в среднем возрастают.

Итак, результаты корреляционного анализа указывают на то, что для запросов ОКС динамические ряды имеют тренд, а для запросов по земельным участкам не имеют.

6.4. Проверка статистических гипотез

6.4.1. Гипотеза о равенстве дисперсий количества запросов на земельные участки и окс.

Необходимость проверки гипотезы о дисперсиях возникает в тех случаях, когда необходимо сравнить стабильностьпроцессов. Если значения признаков (или уровней динамического ряда) варьируются в малых пределах, то такой процесс можно считать стабильным. Прогноз стабильного процесса более надежный.

Гипотеза о равенстве дисперсий формально записывается так:

В табл. 5 приведен результат проверки гипотезы.

Таблица 5

Двухвыборочный F-тест для дисперсии
	земельный участок	ОКС
Среднее	232.6906077	93.39226519
Дисперсия	4200.648189	1427.528607
Наблюдения	181	181
df	180	180
F	2.942601759
P(F<=f) одностороннее	8.00254E-13
F критическое одностороннее	1.278706715

Расчетное отклонение оказалось F больше критического: 2.942601759>1.278706715. Значит можно считать, что дисперсии количества запросов отличаются значимо. При этом вероятность того, что будет отвергнута верная гипотеза, равна уровню значимости =0.05.

6.4.2. Гипотеза о равенстве средних значений запросов на земельные участки и окс

Формальная запись гипотезы:

Результат проверки гипотезы приведены в табл. 6.

Таблица 6

Парный двухвыборочный t-тест для средних
	земельный участок	ОКС
Среднее	232.6906077	93.3923
Дисперсия	4200.648189	1427.53
Наблюдения	181	181
Корреляция Пирсона	0.609862586
Гипотетическая разность средних	0
df	180
t-статистика	36.46478697
P(T<=t) одностороннее	2.37019E-85
t критическое одностороннее	1.653363014
P(T<=t) двухстороннее	4.74038E-85
t критическое двухстороннее	1.973230782

Гипотеза о равенстве генеральных средних запросов по земельным участкам и ОКС отклоняется, поскольку t-статистика больше критических значений.

Гипотезу о средних можно сформулировать относительно одного динамического ряда, разбив его на две части. В этом случае мы можем узнать, является ли среднее значение динамического ряда постоянным на всем интервале наблюдения. Если гипотеза будет отклонена, то это указывает на наличие тренда. Приведем результаты проверки таких гипотез относительно средних динамических рядов запросов.

Для проверки гипотезы о средних по запросам на земельные участки применим двухвыборочный t-тест с одинаковыми дисперсиями. Использование этого теста оправдано, поскольку в предыдущем пункте мы убедились, что дисперсия по запросам на земельные участки постоянная на всем интервале наблюдения. Результаты анализа приведены во фрагменте отчета:

t-статистика	24,98051403
t критическое одностороннее	1,649097299
t критическое двухстороннее	1,966575389

Видно, что t-статистика значительно превышает критические величины. Следовательно, гипотеза о постоянстве средних на всем интервале наблюдения нужно отклонить. Среднее значение количества заявок на земельные участки изменяется во времени. Существует тренд.

Для проверки аналогичной гипотезы относительно средних по запросам на ОКС нужно использовать двухвыборочный t-тест с различными дисперсиями, потому что в п. 6.4.1 было доказано, что дисперсия по запросам на ОКС значимо изменяется на интервале наблюдения. Результаты проверки гипотезы:

t-статистика		24,98051403
t критическое одностороннее	1,650124931
t критическое двухстороннее	1,968177834

И в этом случае гипотезу о постоянстве среднего нужно отклонить – t-статистика превышает критические значения. Так же существует тренд.