5. Элементы алгебры высказываний Основные определения и понятия темы

Высказывание, отрицание высказывания, конъюнкция высказываний, дизъюнкция высказываний, импликация высказываний, эквиваленция высказываний, формула логики высказываний, тождественно истинная формула логики высказываний, тождественно ложная формула логики высказываний, выполнимая, опровержимая формула логики высказываний, равносильные формулы, логическое следствие.

Основные теоремы и утверждения темы

Теорема о свойствах операций над высказываниями.

Рекомендуемая литература

1. Конспект лекций О.Б. Лупанова по курсу «Введение в математическую логику». – М.: Изд-во ЦПИ при механико-математическом факультете МГУ им. М.В. Ломоносова. – 2007.

2. Игошин В.И. Математическая логика и теория алгоритмов. Саратов: Саратовский университет, 1991.

3. Игошин В.И. Задачник-практикум по математической логике. М.: Просвещение, 1986.

4. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Наука, 1975.

Задание 5.1. Составить таблицу истинности для формулы α. Определить, является ли данная формула тождественно истинной, тождественно ложной, выполнимой, опровержимой:

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

17. .

18. .

19. .

20. .

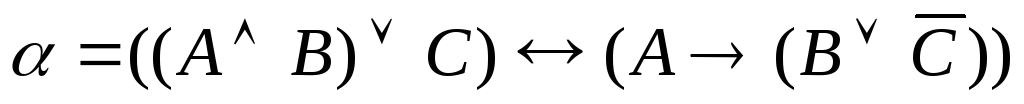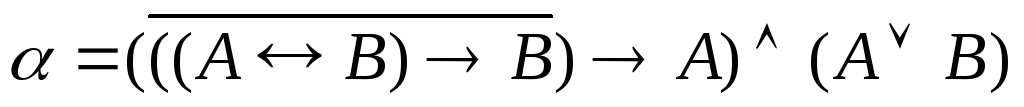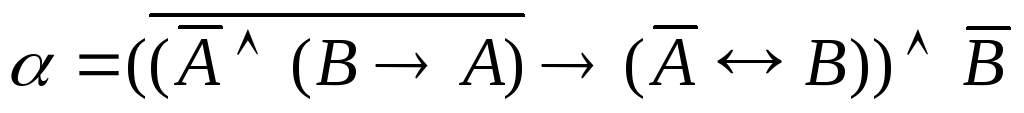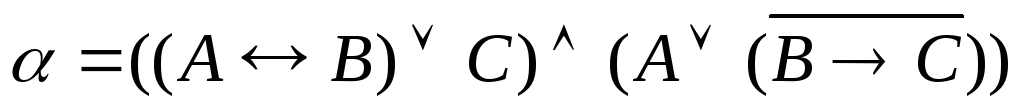Задание 5.2. Доказать равносильность формул илогики высказываний двумя способами:

• с помощью таблицы истинности;

• с помощью свойств операций над высказываниями.

1. , .

2. , .

3. .

4. , .

5. , .

6. , .

7. , .

8. , .

9. , .

10. , .

11. , .

12. , .

13. , .

14. , .

15. , .

16. , .

17. , .

18. , .

19. , .

20. , .

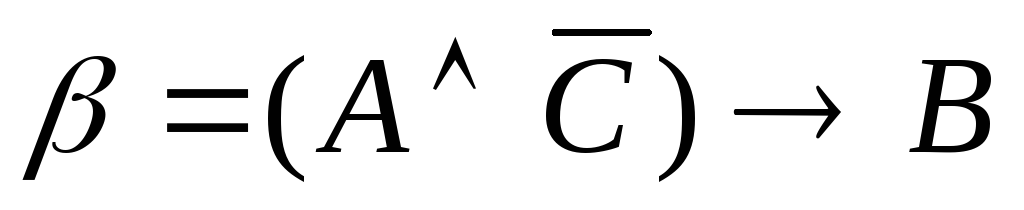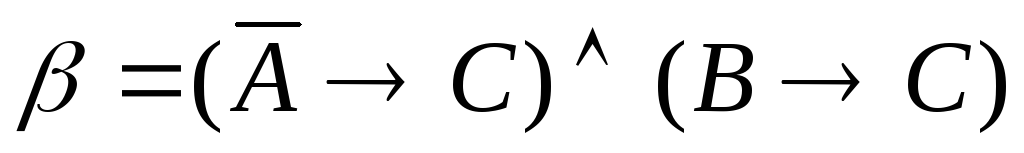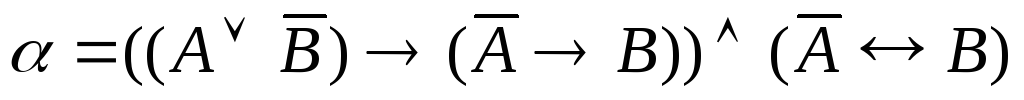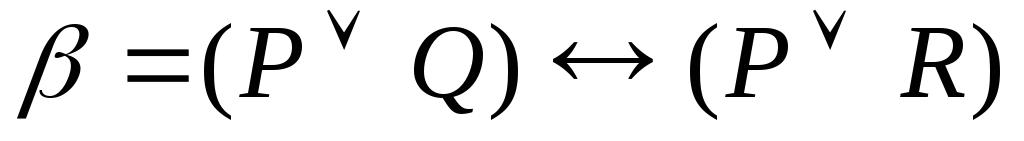Задание 5.3. Проверить, логично ли проведены следующие рассуждения:

1. Если гражданин законопослушен, то он не совершит преступления. Гражданин Иванов – не законопослушен. Значит, он совершит преступление.

2. Если бы он не пошел в кино, то он не получил бы двойки. Если бы он подготовил домашнее задание, то не пошел бы в кино. Он получил двойку. Значит, он не подготовил домашнее задание.

3. Дима или заболел, или не выучил уроки. Если Дима болеет, то он не идет в школу. Дима пошел в школу. Следует ли отсюда, что он выучил уроки?

4. Если Маша идет в библиотеку и замок в ее портфеле исправен, то Маша берет с собой портфель. Завтра Маша пойдет в библиотеку, а замок в портфеле исправен не будет. Следует ли отсюда, что Маша не возьмет с собой портфель?

5. Если будет инфляция, то заработная плата увеличится. Если инфляции не будет, то уменьшатся налоги. Следовательно, либо заработная плата увеличивается, либо уменьшаются налоги.

6. Или Иванов победит в соревнованиях, или Петров выиграет в лотерее. Если Иванов победит в соревнованиях, то его наградят грамотой. Если Петров выиграет в лотерее, то он получит приз. Следует ли отсюда, что либо Иванова наградят грамотой, либо Петров получит приз?

7. Если 1 – натуральное число, то 1 – наименьшее натуральное число. Если 1 – наименьшее натуральное число, то 0 не является натуральным числом. Число 0 не является натуральным. Следует ли отсюда, что 1 – наименьшее натуральное число? Следует ли отсюда, что 1 – натуральное число?

8. Если человек осужден судом, то он лишается избирательных прав. Если человек признан невменяемым, то он также лишается избирательных прав. Следовательно, если человек обладает избирательным правом, то он здоров и не был осужден судом.

9. Иванов утверждает, что не встречал этой ночью Сидорова. Если Иванов не встречал этой ночью Сидорова, то либо Сидоров был убийцей, либо Иванов лжет. Если Сидоров не был убийцей, то Иванов не встречал его этой ночью, а убийство было совершено после полуночи. Если убийство было совершено после полуночи, то либо Сидоров был убийцей, либо Иванов лжет. Следовательно, убийцей был Сидоров.

10. Для того чтобы сдать экзамен, мне необходимо достать конспект. Я достану конспект только в том случае, если мой приятель не уедет. Мой приятель уедет, только если я сдам экзамен. Следовательно, я сдам экзамен.

11. Если я пойду завтра на первое занятие, то должен буду рано встать, а если я пойду вечером на дискотеку, то лягу спать поздно. Если я лягу спать поздно и встану рано, то буду вынужден довольствоваться пятью часами сна. Значит, я должен или пропустить завтра занятие, или не ходить вечером на дискотеку.

12. Если будет холодно, то я надену теплое пальто, если рукав будет починен. Завтра будет холодно, а рукав не будет починен. Следовательно, я не надену теплое пальто.

13. Андрей или очень переутомился, или болен. Если он переутомился, то он раздражается. Он не раздражается. Следовательно, Андрей не болен.

14. Если Антон ляжет спать сегодня поздно, то утром он будет в нерабочем состоянии. Если он ляжет не поздно, то ему будет казаться, что он много времени теряет бесполезно. Следовательно, или Антон завтра будет в нерабочем состоянии, или ему будет казаться, что он много времени теряет напрасно.

15. Если выиграет самарский «Спартак», то Самара будет торжествовать. Если же выиграет саратовский «Сокол», то торжествовать будет Саратов. Выиграет или «Спартак», или «Сокол». Однако если выиграет «Спартак», то Саратов не будет торжествовать, а если выиграет «Сокол», то торжествовать не будет Самара. Следовательно, Самара будет торжествовать тогда и только тогда, когда не будет торжествовать Саратов.

16. Или Анна и Антон одного возраста, или Анна старше Антона. Если Анна и Антон одного возраста, то Наташа и Антон не одного возраста. Если Анна старше Антона, то Антон старше Николая. Значит, либо Наташа и Антон не одного возраста, либо Антон старше Николая.

17. Если 6 – составное число, то 12 также составное число. Если 12 – составное число, то существует простое число больше, чем 12. Если существует простое число больше 12, то существует составное число больше 12. Если 6 делится на 2, то 6 – составное число. Число 12 составное. Следовательно, 6 – составное число.

18. Если я поеду автобусом, а автобус опоздает, то я пропущу назначенное свидание. Если я пропущу назначенное свидание и начну огорчаться, то мне не следует ехать домой. Если я не получу работу, то я начну огорчаться и мне следует поехать домой. Следовательно, если я поеду автобусом, и автобус опоздает, то я получу работу.

19. Если Александр выиграет теннисный турнир, то он будет доволен, а если он будет доволен, то он плохой борец в последующих турнирах. Но если он проиграет этот турнир, то потеряет поддержку своих болельщиков. Он плохой борец в последующих турнирах, если потеряет поддержку своих болельщиков. Если он плохой борец в последующих турнирах, то ему следует прекратить занятия теннисом. Александр или выиграет этот турнир, или проиграет его. Следовательно, ему нужно прекратить занятия теннисом.

20. Если цех II не будет участвовать в выпуске нового образца продукции, то не будет участвовать и цех I. Если же цех II будет участвовать в выпуске нового образца, то в этой работе непременно должны быть задействованы цехи I и III. В выпуске нового образца будет участвовать цех I. Следовательно, необходимо участие в работе цеха III.

Задание 5.4.

1. Четверо задержанных (Михайлов, Костин, Викторов, Тимофеев) подозреваются в краже. На вопрос следователя «Кто совершил кражу?» были получены такие ответы:

   1. «Это сделал или Михайлов, или Костин»,

   2. «Это сделал или Викторов, или Костин»;

   3. «Это не могли сделать ни Тимофеев, ни Михайлов»;

   4. «Это сделали или Викторов, или Михайлов».

Можно ли по этим данным установить, кто виновен в совершении преступления, если известно, что из четырех высказываний три истинны?

2. Разбирается дело Иванова, Петрова и Сидорова. Один из них совершил преступление. В процессе расследования каждый из них сделал по два заявления.

Иванов: Я не делал этого. Петров не делал этого.

Петров: Сидоров сделал это. Иванов не делал этого.

Сидоров: Я не делал этого. Иванов сделал это.

Далее было установлено, что один из них дважды солгал, другой дважды сказал правду, а третий раз солгал, раз сказал правду. Кто совершил преступление? Какой будет ответ, если каждый из них один раз сказал правду, а один раз солгал?

2. В деле об убийстве имеются двое подозреваемых – Иванов и Петров. Допросили четырех свидетелей, которые последовательно дали такие показания: «Иванов не виноват», «Петров не виноват», «Из двух первых показаний, по меньшей мере, одно истинно», «Показания третьего ложны». Четвертый свидетель оказался прав. Кто виновен?

3. На складе совершено хищение. Подозрение пало на трех человек: a, b и c, они были доставлены для допроса. Установлено следующее:

• Никто, кроме a, b, c, не был замешан в деле.

• а никогда не ходит на дело без, по крайней мере, одного соучастника.

• с не виновен.

Виновен ли b?

5. В одном городе было совершено ограбление квартиры. Подозрение пало на двух известных воров – Иванова и Петрова. Кроме того, обнаружились три свидетеля, которые заявили:

Первый: Это они сделали вместе.

Второй: Ограбление совершил Иванов, Петров в этом не участвовал.

Третий: Если Петров совершил ограбление, то Иванов тоже принимал в этом участие.

Какой вывод можно сделать из показаний свидетелей, если выяснилось, что все они врали?

6. Выяснить, кто из четверых виновен на основе информации: «Петров виновен, только если виновен Иванов. Неверно, что виновность Сидорова влечет виновность Родионова и что Иванов виновен, а Сидоров нет».

7. По подозрению в совершенном преступлении задержали Иванова, Петрова и Сидорова. Один из них был уважаемым в городе стариком, другой был малоизвестным чиновником, третий – известным мошенником. В процессе следствия старик говорил правду, мошенник лгал, а третий задержанный в одном случае говорил правду, а в другом – ложь. Вот, что они утверждали:

Иванов: Я совершил это. Петров не виноват

Петров: Иванов не виноват. Преступление совершил Сидоров.

Сидоров: Я не виноват. Виноват Иванов.

Требуется определить фамилии старика, чиновника и мошенника, и кто из них виноват, если известно, что преступник один.

8. По подозрению в преступлении задержаны трое подозреваемых: Иванов, Петров, Сидоров. В ходе следствия обнаружились два свидетеля. На вопрос следователя «Кто совершил преступление?» были получены такие ответы:

Первый свидетель: «Это мог сделать только или Иванов, или Петров».

Иванов: «Я этого не совершал, и Сидоров тоже».

Петров: «Вы оба говорите неправду».

Второй свидетель: «Нет, Петров, один из них солгал, а один сказал правду».

Сидоров: «Нет, второй свидетель не прав».

Кто совершил преступление, если известно, что трое из них сказали правду?

9. На вопрос: «Кто из трех подозреваемых совершил преступление?» получен правдивый ответ: «Если виновен первый, то виновен и третий, но не верно, что если виновен второй, то виновен и третий». Кто виновен?

10. Определите, кто из четырех преступников участвовал в ограблении, если известно:

• если первый участвовал, то и второй тоже участвовал;

• если участвовал второй, то третий участвовал или первый не участвовал;

• если четвертый не участвовал, то первый участвовал, а третий не участвовал;

• если четвертый участвовал, то и первый участвовал.

Задание 5.5.

1. Предположим, что а говорит: «Или я лжец, или b рыцарь». Кто из двух персонажей – а и b – рыцарь и кто лжец?

2. Предположим, что а высказывает утверждение: «Я – лжец, а b не лжец». Кто из персонажей – а и b – рыцарь и кто лжец?

3. Предположим, что а утверждает: «Если b – рыцарь, то я лжец». Кто из персонажей – а и b – рыцарь и кто лжец?

4. Предположим, что а утверждает: «Если b – лжец, то я рыцарь». Можно ли установить, кто есть кто?

5. Предположим, что а утверждает: «Если я – лжец, то и b – лжец». Можно ли установить, кто есть кто?

6. Известно, что каждый из a, b, c является либо рыцарем, либо лжецом. Можно ли определить, кто есть кто по их следующим высказываний:

а: «Мы все лжецы».

b: «Только один из нас – лжец».

7. Предположим, что а утверждает: «Если я – рыцарь, то и b – рыцарь». Убедиться, что а и b рыцари.

8. Известно, что каждый из a, b, c является либо рыцарем, либо лжецом. Можно ли определить, кто есть кто по их следующим высказываний:

а: «Мы все рыцари».

b: «Только один из нас – рыцарь».

9. На некотором острове, населенном рыцарями и лжецами, разнесся слух о том, что на нем зарыты сокровища. Вы прибываете на остров и спрашиваете одного из местных жителей: «Есть ли на острове золото?». В ответ на ваш вопрос он заявляет: «Сокровища на этом острове есть в том и только в том случае, если я рыцарь». Можно ли определить, кто такой этот местный – рыцарь или лжец? Можно ли определить, есть ли на острове сокровища?

10. Один из а, b и с является рыцарем, один лжецом, один – нормальным человеком (нормальные люди иногда лгут, иногда говорят правду). Они утверждают следующее:

а: «Я нормальный человек».

b: «То, что сказал а – правда».

с: «Я – не нормальный человек».

Кем являются а, b и с в действительности?