
rgr5
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ И СТРОИТЕЛЬНОЙ МЕХАНИКИ
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПРИ ПЛОСКОМ ИЗГИБЕ
Методические указания и задания к расчетно-графической работе по курсу “Сопротивление материалов” для студентов 2-го курса всех строительных
специальностей очной формы обучения
Краснодар
2007
Составители: д-р. физ.-мат. наук, проф. Н. Н. Фролов, канд. физ.-мат. наук, доц. С. Ю. Молдаванов, канд. физ.- мат. наук, доц. С.Б. Лозовой
УДК 539.3
Определение перемещений при плоском изгибе. Методические указания и задания к расчетно-графической работе по курсу «Сопротивление материалов» для студентов 2-го курса всех строительных специальностей очной формы обучения / Сост.: Н.Н. Фролов, С.Ю. Молдаванов, С.Б. Лозовой; Кубан. гос. технол. ун-т. Каф. сопротивления материалов и строительной механики. − Краснодар: Изд. КубГТУ, 2007. − 38 с.
Предлагаемые методические указания посвящены изучению методов определения перемещений при плоском изгибе. Для вычисления прогибов и углов поворота используются метод начальных параметров и графо-аналити- ческий метод. Приведены примеры решения типовых статически определимых и статически неопределимых задач, входящих в состав расчетно-графи- ческой работы по курсу «Сопротивление материалов». Предназначены для студентов 2-го курса всех строительных специальностей очной формы обучения.
Ил. 16. Табл. 2.
Печатается по решению Редакционно-издательского совета Кубанского государственного технологического университета
Рецензенты: канд. техн. наук, доц. кафедры строительных конструкций и гидротехнических сооружений КубГТУ С.И. Дизенко;
канд. техн. наук, доц. кафедры сопротивления материалов и строительной механики КубГТУ В. В. Попов
2
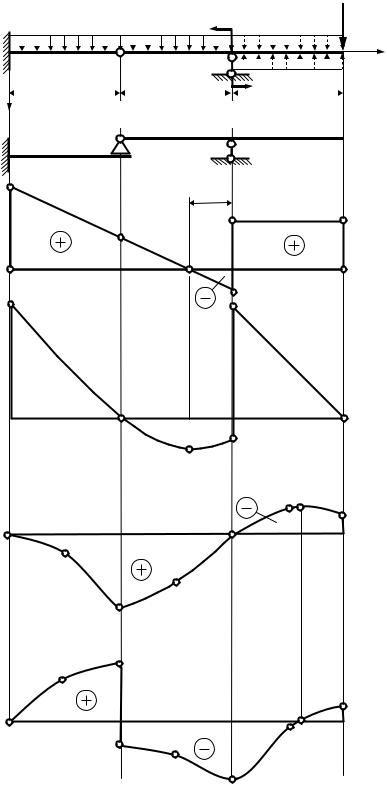
1. МЕТОД НАЧАЛЬНЫХ ПАРАМЕТРОВ
Построить эпюры прогибов и углов поворота для заданной балки с помощью уравнений метода начальных параметров.
|
q=2 кН/м |
М=12 кНм |
F=5 кН |
|
A |
C |
B |
D |
z |
2 м |
2 м |
2 м |
|
|
y |
Поэтажная схема |
|
|
|
|
D |
|
||
А |
|
B |
|
|
C |
|
|
||
7 |
|
0,5 |
|
|
|
3 |
5 |
5 |
|
|
|
|
Эп. Qy |
|
10 |
|
1 |
(кН) |
|
|
|
|
||
|
10 |
|
|
|
|
|
|
|
|
|
|
|
Эп. Мх |
|
|
0 |
2 |
(кНм) |
|
|
|
|
||
|
|
|
|
|
|
2,25 |
|
|
|
|
|
3,84 |
2,67 |
|
0 |
|
0 |
Эп. v EJx |
|
|
|
|
||
3,917 |
|
|
|
|
|
6,91 |
|
|
|
|
12,0 |
|
|
|
6,833 |
8,67 |
|
2,02 |
|
|
|
|
||
0 |
|
0,50 |
Эп.θEJx |
|
|
4,67 |
|
|
|
|
5,84 |
8,0 |
|
|
Рисунок 1.1. Использование метода начальных параметров для определения перемещений в балках с врезным шарниром
3
q=2 кН/м |
М=12 кНм F=5 кН |
С |
2 |
B |
3 |
D |
z |
|
|||||
у |
2 м |
|
2 м |
|
|
V =3кН |
|
VВ=6кН |
|
|
|
|
C |
|
|
|
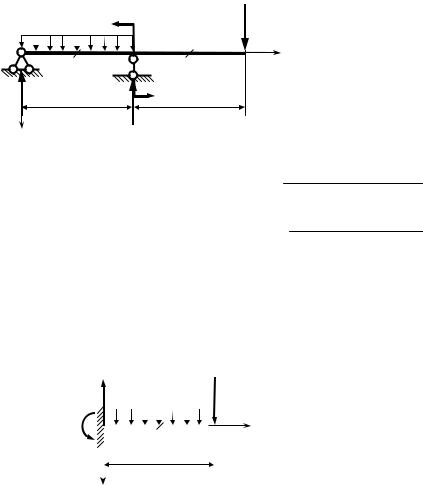
Решение задачи об определении перемещений в многопролетной балке методом начальных параметров начинаем с построения поэтажной схемы. Находим величины опорных реакций отдельных балок, начиная с верхнего этажа поэтажной схемы:
∑mC = 0 ; VB = 2 22 / 2 −212 +5 4 = 6 кН;
∑mB = 0 ; VC = 2 22 / 2 +212 −5 2 = 3кН.
Проверка: ∑у = 0 ; 2 2 +5 −6 −3 = 0 , следовательно, опорные реакции балки
верхнего этажа поэтажной схемы найдены верно. Используя полученные значения опорных реакций, строим эпюры поперечных сил Qy и изгибающих
моментов M x |
в балке второго этажа. |
||||
|
VA=7кН |
|
|
Определяем величину опорных ре- |
|
MA=10кНм q=2 кН/м |
|
V =3кН акций балки нижнего этажа, для чего по- |
|||
|
C |
мимо действия заданных нагрузок учиты- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ваем и ранее вычисленную опорную ре- |
|
A |
1 |
C |
z |
|
|
акцию VC , приложенную в противопо- |
||||
y |
2 м |
|
|
||
|
|
|
ложном направлении. |
||
|
|
|
|||
∑у = 0 ; VA = 2 2 +3 =7 кН,
∑mA =0 ; M A = 2 22 / 2 +3 2 =10 кНм.
Используя полученные значения опорных реакций, строим эпюры поперечных сил Qy и изгибающих моментов M x в балке второго этажа.
Окончательные эпюры поперечных сил Qy и изгибающих моментов M x в заданной балке строятся путем состыковки в точке С ранее построен-
ных эпюр в отдельных балках поэтажной схемы.
При вычислении перемещений в многопролетной балке с помощью метода начальных параметров расчет необходимо начинать с балки, находящейся в нижнем этаже поэтажной схемы. Уравнения метода начальных параметров записываем в следующем виде:
n |
M |
(z |
i |
−a |
)1 |
|
n |
|
F |
(z |
i |
−a |
)2 |
|
|
n |
|
q |
(z |
i |
−a |
)3 |
|
|
|
|
||||
EJ xθi = EJ xθ0 +∑ |
i |
|
i |
|
+∑ |
i |
|
|
i |
|
|
+∑ |
i |
|
|
i |
|
; |
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
6 |
|
|
|
|
||||||||||||
i=1 |
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
n |
M |
(z |
|
−a |
)2 |
n |
F |
(z |
|
−a |
)3 |
|
n |
q (z |
|
− a |
)4 |
|||||||||
EJ x vi = EJ x vo + EJ xθ0 zi + ∑ |
|
i |
|
i |
|
|
i |
|
|
+ ∑ |
|
i |
|
i |
6 |
i |
|
|
+ ∑ i |
i |
i |
. |
||||||||
|
|
|
|
i=1 |
|
|
|
2 |
|
|
|
|
i=1 |
|
|
|
|
|
|
|
i=1 |
|
24 |
|
||||||
4
Начальные параметры балки первого этажа (прогиб и угол поворота сечения в начале координат) определяются из условий ее закрепления. В начале координат имеется защемление, которое препятствует как угловым, так и линейным перемещениям, следовательно, EJ x vo = 0 и EJ xθo = 0 .
Вычисляем перемещения сечений, расположенных в серединах и на границах грузовых участков балки первого этажа:
− z1 =1 м:
EJ θ |
1 |
= 10 (1 −0)1 |
x |
1 |
|
|
|
EJ xv1 = 10 (1 −0)2 2
−zС = 2 м:
EJ xθС = 10 (2 −0)1 1
− |
7 (1 −0)2 |
|
+ 2 (1 −0)3 |
= 6,833; θ1 |
= |
6,833 ; |
||
|
2 |
|
|
6 |
|
|
|
EJ x |
− 7 (1 −0)3 |
+ 2 (1 −0)4 |
= 3,917 ; v |
= 3,917 ; |
|||||
|
6 |
|
|
24 |
|
1 |
|
EJ x |
|
|
|
|
|
|
|||
− |
7 (2 −0)2 |
+ |
2 (2 −0)3 |
=8,67 ; θСлев |
= 8,67 ; |
|||
|
2 |
|
|
6 |
|
|
|
EJ x |
EJ |
v |
|
= 10 (2 −0)2 |
− 7 (2 −0)3 |
+ 2 (2 −0)4 |
=12 ; |
v = |
12 |
. |
С |
|
||||||||
x |
|
2 |
6 |
24 |
|
С |
EJ x |
||
|
|
|
|
|
|||||
При вычислении перемещений в балке второго этажа с помощью метода начальных параметров необходимо устранить разрыв в равномерно распределенной нагрузке. Для чего балку нужно догрузить нагрузкой заданной интенсивности q = 2 кН/м и, и чтобы не изменилось деформированное состояние балки, на том же участке необходимо приложить компенсирующую нагрузку интенсивностьюq = 2 кН/м, направленную в противоположном направлении (см. рис. 1.1).
Следует заметить, что в точке С на эпюре прогибов v имеется излом, а на эпюре углов поворота сечения θ – разрыв. Поэтому при определении перемещений в балке верхнего этажа в качестве одного из начальных параметров (прогиба в начале координат) следует принять EJ xvo = EJ xvС =12 . Второй
начальный параметр EJ xθo = EJ xθСпр ≠ 0 . Угол поворота сечения в начале ко-
ординат необходимо определить из условия опирания балки второго этажа в точке В – при zВ = 2 м; EJ x vВ = 0 , отсюда
EJ |
v |
В |
=12 + EJ θ |
2 |
− 3 (2 −0)3 |
+ 2 (2 −0)4 |
= 0 ; |
||||
x |
|
x 0 |
|
|
|
6 |
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
||
EJ θ |
2 +9,33 = 0 ; |
EJ θ |
|
= − |
9,33 |
= −4,67 =θпр . |
|||||
0 |
|
||||||||||
x |
0 |
|
|
x |
2 |
|
С |
||||
|
|
|
|
|
|
|
|
|
|||
Вычисляем перемещения сечений, расположенных в серединах и на границах грузовых участков балки второго этажа:
5
− |
z2 |
=1 м: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
EJ θ |
= −4,67 − 3 (1 −0)2 |
|
+ 2 (1 −0)3 |
= −5,84 θ |
2 |
|
= −5,84 |
|
|
||||||||||||
|
|
|
x 2 |
|
|
|
2 |
|
|
6 |
|
|
|
|
|
|
EJ x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
EJ x v2 |
=12 −4,67 1 − 3 (1 −0)3 + |
2 (1 −0)4 = 6,91; v2 |
= 6,91 ; |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
6 |
|
24 |
|
|
|
|
|
EJ x |
|
|
|||
− |
zВ = 2м: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
EJ θ |
= −4,67 − 3 (2 −0)2 |
+ 2 (2 −0)3 |
= −8,00 θ |
В |
= −8,00 |
|
|
||||||||||||||
|
|
|
x В |
|
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
EJ x |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
EJ x vВ |
=12 −4,67 2 − 3 (2 −0)3 + 2 (2 −0)4 = −0,01; |
vВ = − |
0,01 ≈0 ; |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
24 |
|
|
|
|
|
|
EJ x |
||
− |
z3 |
= 3 м; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
EJ θ |
= −4,67 − 3 (3 −0)2 |
+ 2 (3 −0)3 |
|
+12 (3 −2)1 |
|
− |
|
|
|
|
|||||||||||
|
|
|
x 3 |
|
|
|
2 |
|
|
6 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
− 6 (3 −2)2 |
− 2 (3 −2)3 |
= −0,50; |
θ3 = −0,50 ; |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
6 |
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
EJ x v3 |
=12 −4,67 3 − 3 (3 −0)3 + 2 (3 −0)4 +12 (3 −2)2 |
− |
|
|
|||||||||||||||||
|
− 6 (3 −2)3 |
− 2 (3 −2)4 |
6 |
24 |
|
|
2 |
|
|
|
|
|||||||||||
|
= −3,84 ; |
v3 = −3,84 ; |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
6 |
|
|
24 |
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
− |
z |
D |
= 4 м; EJ θ |
D |
= −4,67 − 3 (4 −0)2 |
+ 2 (4 −0)3 |
+12 (4 −2)1 |
− |
||||||||||||||
|
|
|
|
x |
|
|
|
2 |
|
|
|
6 |
|
|
|
|
|
1 |
|
|
||
|
− 6 (4 −2)2 |
− 2 (4 −2)3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
= 2,00 ; θD = |
2,00 ; |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
6 |
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
EJ x vD |
=12 −4,67 4 − 3 (4 −0)3 + |
2 (4 −0)4 +12 (4 −2)2 − |
|
|
|||||||||||||||||
|
− 6 (4 −2)3 |
− 2 (4 −2)4 |
|
6 |
|
24 |
|
|
|
2 |
|
|
|
|
||||||||
|
= −2,68; |
vD |
= −2,68 . |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
6 |
|
|
24 |
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
По полученным значениям строим эпюру углов поворота сечения θ и эскиз упругой линии балки v (см. рис.1.1). Сравнивая эпюры перемещений, построенные методом начальных параметров и графо-аналитическим методом можно сделать вывод об их полной идентичности. Некоторые погрешности при определении ординат рассматриваемых эпюр связаны с округлением чисел при вычислениях. Сравнивая два метода определения перемещений можно сделать вывод, что метод начальных параметров позволяет вычислять искомые величины в любой точке балки, а графо-аналитический – только на границах грузовых участков.
6
2. ГРАФО-АНАЛИТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ В БАЛКАХ
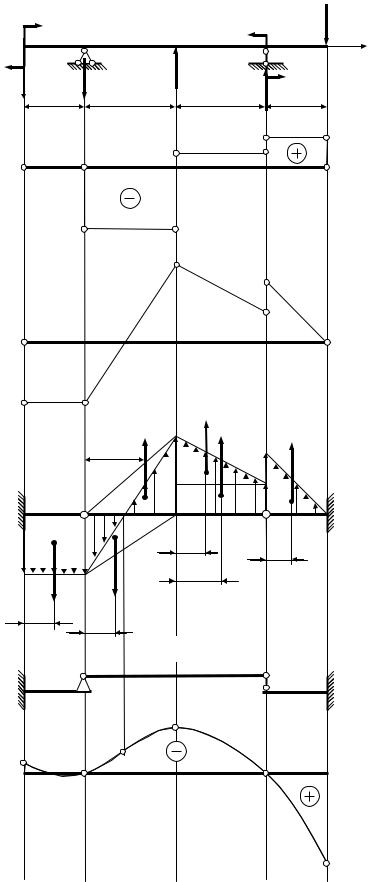
Построить эпюры прогибов и углов поворота для заданной балки с помощью уравнений метода начальных параметров (рис. 2.1).
Определяем величину опорных реакций заданной балки:
∑mВ = 0; VА = |
20 +20 3 −10 +10 2 |
=15кН; |
||
4 |
|
|||
|
|
|
||
∑mА = 0 ; VВ = |
|
20 +10 8 −10 −20 3 |
=5 кН. |
|
4 |
|
|||
|
|
|
||
Проверка∑: y =0 ; VA −VB − F1 + F2 = 0; 15 −20 +10 −5 = 0 . |
||||
Используя полученные значения опорных реакций, строим эпюры по- |
||||
перечных сил Qy и изгибающих моментов M x в заданной балке.
Принимаем схему фиктивной балки в соответствии с условиями закрепления заданной балки. Фиктивную балку загружаем фиктивной распределенной нагрузкой, изменяющейся по закону изгибающего момента M x в за-
данной балке. Фиктивную распределенную нагрузку направляем от оси балки в сторону растянутых волокон заданной балки. Ординатами фиктивной распределенной нагрузки являются ординаты эпюры M x , деленные на вели-
чину изгибной жесткости EJ x .
Площадь фиктивной распределенной нагрузки разбиваем на элементарные геометрические фигуры – треугольники и прямоугольники. Действие каждого из элементарных участков фиктивной распределенной нагрузки заменяем равнодействующими ωi . Величина равнодействующей ωi равняется
площади соответствующего элемента фиктивной распределенной нагрузки. Точки приложения равнодействующих находятся в центрах тяжести элементов фиктивной распределенной нагрузки. Находим величины равнодействующих ωi и координаты точек их приложения ai :
ω1 = |
20 |
|
|
|
2 = |
40 |
; |
|
а = 2 1 |
=1 м; |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
EJ x |
|
|
|
EJ x |
|
|
|
1 |
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ω2 = |
|
20 |
|
|
|
3 |
= |
|
30 |
|
|
; |
|
а2 |
= 3 |
1 |
=1 м; |
|||||||
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
EJ x |
|
|
|
|
EJ x |
|
|
|
|
|
3 |
|
||||||||||
ω3 = |
|
25 |
|
|
|
3 |
= |
|
37,5 |
; |
|
а3 |
=3 |
2 |
= 2 м; |
|||||||||
|
|
|
2 |
|
|
EJ x |
||||||||||||||||||
|
|
EJ x |
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||||
ω4 = |
|
(25 −10) |
|
|
3 |
= |
|
|
|
22,5 |
; |
а4 |
= 3 |
1 |
=1 м; |
|||||||||
|
|
|
2 |
|
|
|
|
|||||||||||||||||
|
|
EJ x |
|
|
|
|
|
|
|
|
EJ x |
|
|
3 |
|
|||||||||
ω5 = |
|
10 |
3 = |
|
30 |
; |
|
а5 |
= 3 |
1 |
=1,5 м; |
|||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
EJ x |
|
|
|
EJ x |
|
|
|
|
|
2 |
|
|||||||||||
7
ω6 = |
20 |
|
2 |
= |
20 |
. |
а6 |
= 2 |
1 |
= 0,67 м. |
|
2 |
|
||||||||
|
EJ x |
|
EJ x |
|
|
3 |
|
|||
Для определения опорных реакций фиктивной балки составляем поэтажную схему, позволяющую установить порядок взаимодействия между отдельными элементами многопролетной системы. Построение поэтажной схемы поводится в следующем порядке: через врезные шарниры мысленно проводят сечения и выявляют элементарные балки, которые могут самостоятельно нести внешнюю нагрузку, без участия остальных элементов. К таким элементам относятся консольные балки и балки на двух опорах. Указанные балки располагают в нижнем этаже поэтажной схемы, а остальные элементы помещают в следующих этажах в соответствии с порядком их примыкания. Балки, не имеющие промежуточных опор, располагаются в самом верхнем этаже поэтажной схемы. Расчет начинаем с балки, расположенной в самом верхнем этаже поэтажной схемы (балка АВ).
Определяем величину опорных реакций фиктивной балки АВ: |
|||||||||||||
∑mB = 0; |
VAfic = ω3 (6 −a3 )+ω4 (3 −a4 ) |
+ω5 (3 −a5 ) |
−ω2 |
(6 −a2 )= |
|||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
1 |
|
37,5 (6 −2)+22,5 (3 −1)+30 (3 −1,5)−30 (6 −1) |
15 |
|
2 |
|||||||
= |
|
|
|
|
|
|
|
= |
|
|
|
кНм ; |
|
|
|
6 |
|
|
EJ x |
||||||||
|
EJ x |
|
|
|
|
|
|||||||
|
∑mА = 0; |
VBfic = |
ω3 a3 +ω4 (3 + a4 )+ω5 (3 + a5 )−ω2a2 |
|
= |
||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
= |
|
1 37,5 2 + 22,5 (3 +1)+30 (3 +1,5)−30 1 |
45 |
|
|
|
2 |
|||||
|
|
|
|
|
|
= |
|
|
|
кНм . |
|||
|
|
|
6 |
|
EJ x |
|
|||||||
|
|
|
EJ x |
|
|
|
|
|
|
||||
Находим величину опорных реакций фиктивной балки СА, расположенной в первом этаже поэтажной схемы. Опорные реакции балки АВ, расположенной в верхнем этаже поэтажной схемы, прикладываем к балке СА в противоположном направлении. Тогда:
∑mС =0 ; MCfic =ω1a1 −VAfic 2 = |
1 |
|
(40 1−15 2)= |
10 |
кНм3; |
||
EJ x |
|
||||||
|
|
|
|
|
EJ x |
||
∑y =0 ; VCfic =ω1 −VAfic = |
1 |
|
(40 −15)= |
25 |
|
кНм2. |
|
EJ x |
|
EJ x |
|||||
|
|
|
|
|
|||
Определяем величину опорных реакций фиктивной балки ВЕ, расположенной в первом этаже поэтажной схемы. Опорные реакции балки АВ, расположенной в верхнем этаже поэтажной схемы, прикладываем к балке ВЕ в противоположном направлении, получаем:
∑mE =0 ; M Efic =ω6 (2 −a6 )+VBfic 2 = |
|
|
1 |
[20 (2 −0,67)+45 |
2]= |
116,7 кНм3; |
||||
|
|
|
|
|||||||
|
|
EJ x |
|
|
|
|
EJ x |
|||
∑y =0 ; VEfic =ω6 +VBfic |
= |
|
1 |
(20 +45)= |
65 |
|
кНм2. |
|||
|
EJ x |
EJ x |
||||||||
|
|
|
|
|
|
|
||||
8
М1=20 кНм |
|
|
|
|
|
|
F2=10 кН |
|
|
|
F1=20 кН |
М2=10 кНм |
|||||
|
|
|
|
|||||
C |
|
|
|
|
|
z |
||
|
|
|
|
D |
B |
|
E |
|
|
A |
RA=15 кН |
|
|||||
y |
RB=5 кН |
|
|
|||||
2 м |
|
3 м |
|
3 м |
2 м |
|||
|
|
|
||||||
|
|
|
|
|
|
10 |
|
10 |
|
|
|
|
5 |
|
5 |
|
Эп.Qy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(кН) |
|
20 |
|
|
|
20 |
|
|
|
|
|
|
|
|
25 |
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
Эп.Mx |
|
|
|
|
|
|
|
|
(кНм) |
20 |
|
20 |
EJ25x |
ω4 |
|
20 |
|
|
|
|
ω |
ω |
ω6 |
||||
|
|
|
a3 |
3 |
|
510 |
EJx |
|
|
|
|
|
|
EJx |
|
|
|
|
|
|
|
|
|
|
|
|
C |
A |
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
B |
|
|
|
|
|
|
|
a4 |
|
a6 |
|
|
|
|
|
|
a5 |
|
|
|
20 |
|
20 |
ω2 |
|
|
|
||
ω1 |
|
|
|
|
||||
EJx |
EJx |
|
|
|
|
|
|
|
|
a1 |
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
Поэтажная схема |
B |
E |
||
C |
|
|
|
D |
|
|||
|
|
|
67,5 |
|
|
|
||
|
|
|
|
|
|
|
||
10 |
|
|
|
EJx |
|
|
|
|
|
|
|
|
|
|
|
|
|
EJx |
0 |
|
|
|
|
|
0 |
Эп.v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
116,7 |
|
|
|
|
|
|
|
|
EJx |
|
|
|
|
|
9 |
|
|
|

3. ПРИМЕНЕНИЕ ГРАФО-АНАЛИТИЧЕСКОГО МЕТОДА ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ В БАЛКАХ
С ВРЕЗНЫМ ШАРНИРОМ Определяем величину опорных реакций заданной балки:
∑mСпр = 0; VВ = |
2 22 / 2 −12 +5 4 |
=6 кН; |
|
2 |
|
∑mА = 0 ; МА = 2 42 / 2 +5 6 −6 4 −12 =10 кНм;
∑mСлев = 0; VА = 2 22 /22 +10 =7 кН.
Проверка:
∑y =0 ; −VA −VB + F +q 2 =0 ; −7 −6 +5 +2 4 =0 , следовательно, опорные реакции найдены верно.
Используя полученные значения опорных реакций, строим эпюры поперечных сил Qy и изгибающих моментов M x в заданной балке.
Принимаем схему фиктивной балки в соответствии с условиями закрепления заданной балки. Фиктивную балку загружаем фиктивной распределенной нагрузкой, изменяющейся по закону изгибающего момента M x в за-
данной балке. Фиктивную распределенную нагрузку направляем от оси балки в сторону растянутых волокон заданной балки. Ординатами фиктивной распределенной нагрузки являются ординаты эпюры M x , деленные на вели-
чину изгибной жесткости EJ x .
Площадь фиктивной распределенной нагрузки разбиваем на элементарные геометрические фигуры – треугольники и параболические сегменты. Действие каждого из элементарных участков фиктивной распределенной нагрузки заменяем равнодействующими ωi . Величина равнодействующей ωi
равняется площади соответствующего элемента фиктивной распределенной нагрузки. Точки приложения равнодействующих находятся в центрах тяжести элементов фиктивной распределенной нагрузки.
Находим величины равнодействующих ωi и координаты точек их приложения ai :
ω1 = |
10 |
|
|
2 = |
10 |
; |
|
|
а = 2 2 |
=1,33 м; |
|||||||
|
|
|
|
|
|
|
|||||||||||
|
EJ x |
2 |
|
EJ x |
|
|
1 |
|
3 |
|
|||||||
|
|
|
|
|
|
|
|||||||||||
ω2 = |
|
1 |
|
ql3 |
= |
2 23 |
= |
1,33 ; |
а2 |
= 2 |
1 |
=1 м; |
|||||
|
|
|
|
|
2 |
||||||||||||
|
|
EJ x |
12 |
|
12EJ x |
|
EJ x |
|
|
|
|||||||
ω3 = |
|
2 |
|
2 = |
|
2 |
; |
|
|
а3 |
= 2 |
1 |
= 0,67 м; |
||||
|
|
|
|
|
|||||||||||||
|
|
EJ x |
2 |
|
EJ x |
|
|
|
|
3 |
|
||||||
10
