2. Примеры решения задач

1. Решить задачу Коши.

.

◄ Заменяя на,на,на, получаем характеристическое уравнение. Его корни,действительны и имеют кратности 1. Поэтому– фундаментальная система решений, а общее решение уравнения имеет вид

.

Найдем . Подставляя в выражения дляиначальное значение, получим

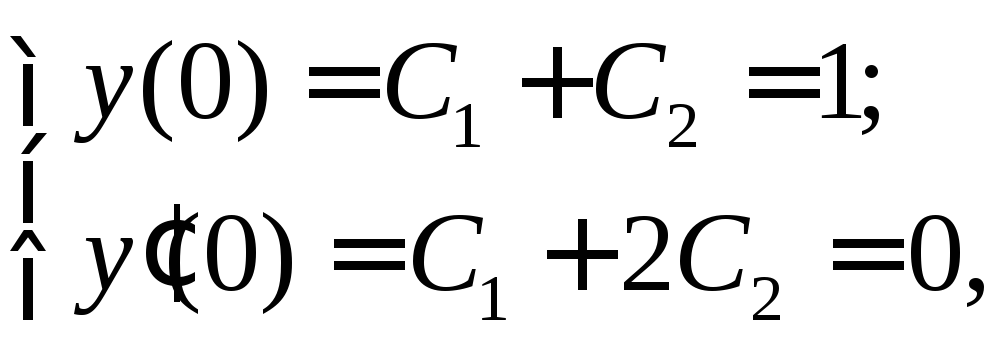
откуда находим . Таким образом, решение задачи Коши имеет вид.►

2. Решить уравнение .

◄ Характеристическое уравнение .

–корень кратности 2.

–ф.с.р.

–общее решение. ►

3. Решить уравнение .

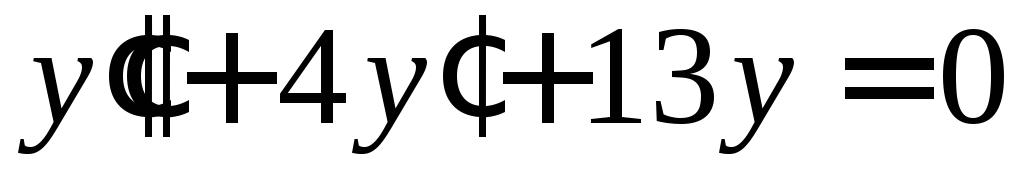◄ Характеристическое уравнение имеет комплексные сопряженные корни. Поэтому

–ф.с.р., а

–общее решение. ►

4. Решить уравнение .

◄ Характеристическое уравнение . Его корни,. Корнюсоответствует в фундаментальной системе решение, паре комплексных сопряженных корней– решения,. Общее решение.►

3. Задачи для самостоятельного решения

Решить уравнения.

.	.
	.
.	.
, .	.
,.	,.
.	.
.

13. Линейные неоднородные дифференциальные уравнения n-го порядка. Метод неопределенных коэффициентов

1. Сведения из теории

Общее решение линейного неоднородного дифференциального уравнения n-го порядка

можно представить в виде

,

где – какое-нибудь частное решение уравнения , а– ф.с.р. соответствующего линейного однородного уравнения

Иными словами, общее решение линейного неоднородного уравнения – сумма его частного решения и общего решения линейного однородного уравнения .

Рассмотрим часто встречающееся в приложениях уравнение с постоянными коэффициентами и правой частью вида

,

где ,– многочлены.

Частное решение такого уравнения можно искать в виде

,

где ,– многочлены с неопределенными (буквенными) коэффициентами степени; показатель, если корни характеристического уравнения не совпадают с, иравно кратности корняхарактеристического уравнения, если. Заметим, что при решении конкретных задач коэффициенты многочленовиобычно удобнее обозначать не одной буквой с индексом, как выше, а разными буквами, например

Рассмотрим некоторые частные случаи.

Таблица. Частные случаи правых частей

И соответствующие им частные решения

	Вид правой части		Вид частного решения
1
2
3			, .

Если правая часть уравнения – сумма функций вида

,

то частное решение ищется в виде суммы функций вида