
- •Кафедра высшей математики
- •Обыкновенные дифференциальные уравнения
- •Дифференциальные уравнения первого порядка. Общие понятия
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Уравнения с разделяющимися переменными
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Замена переменных в дифференциальных уравнениях первого порядка
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Однородные уравнения
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные уравнения первого порядка
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Смешанные задачи на дифференциальные уравнения первого порядка
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Дифференциальные уравнения высших порядков
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Линейные однородные дифференциальные уравнения n-го порядка
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные однородные уравнения с постоянными коэффициентами
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные неоднородные дифференциальные уравнения n-го порядка. Метод неопределенных коэффициентов
- •Сведения из теории
- •И соответствующие им частные решения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные неоднородные дифференциальные уравнения n-го порядка. Метод вариации произвольных постоянных
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Список литературы
- •5.3.9. А); б).
- •Вариант 1
- •150023, Ярославль, Московский пр., 88
Задачи для самостоятельного решения
Убедиться, что
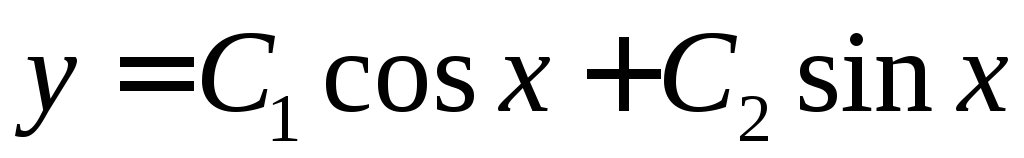 является общим решением уравнения
является общим решением уравнения .
Найти а) решение, удовлетворяющее
начальным условиям
.
Найти а) решение, удовлетворяющее
начальным условиям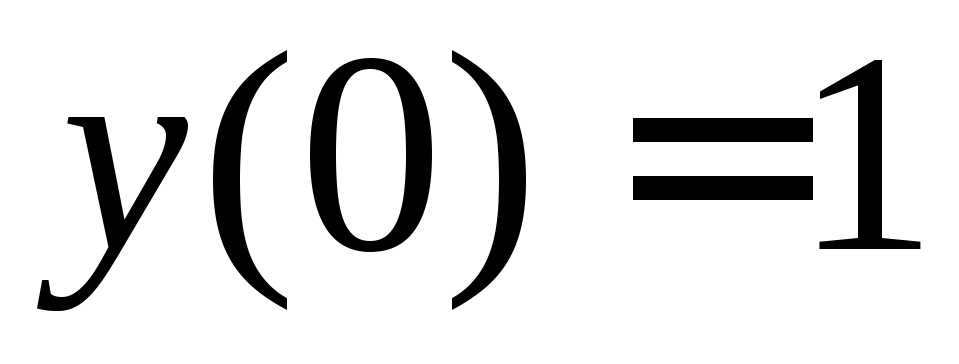 ,
,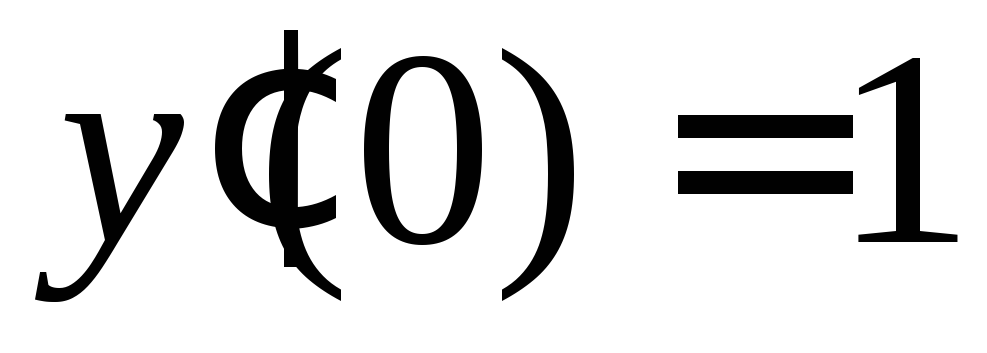 ;
б) решение, удовлетворяющее граничным
условиям
;
б) решение, удовлетворяющее граничным
условиям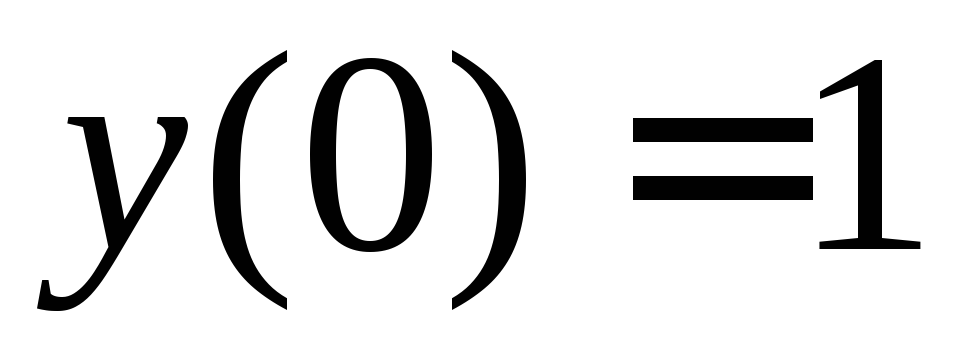 ,
,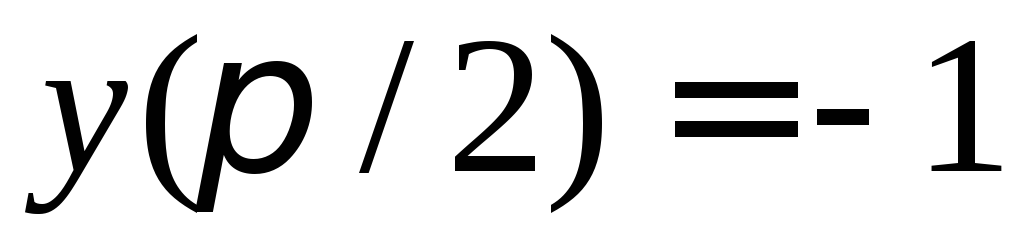 .
.
Дифференциальные уравнения,
допускающие понижение порядка
Сведения из теории
Укажем несколько типов дифференциальных уравнений, которые заменой переменных можно свести к уравнениям меньшего порядка.
Простейшее дифференциальное уравнение n-го порядка
Это
уравнение вида
![]() .
Его общее решение находитсяn-кратным
интегрированием
.
Его общее решение находитсяn-кратным
интегрированием
![]() ,
,
![]() ,
,
…………..
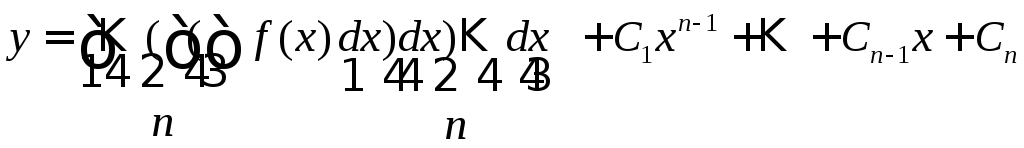 .
.
Уравнение n-го порядка, не содержащее явно искомой функции
и
ее производных до
![]() -го
порядка включительно
-го
порядка включительно
![]() .
.
Его
можно рассматривать как уравнение
![]() -го
порядка относительно функции
-го
порядка относительно функции![]() :
:
![]() .
.
Пусть
![]() – его общее решение. Тогда общее решение
– его общее решение. Тогда общее решение![]() уравнения находится из уравнения
уравнения находится из уравнения
![]()
k-кратным интегрированием, в соответствии с п. 10.1.1.
Уравнение второго порядка, не содержащее явно
независимой переменной x
![]() .
.
Введем
новую неизвестную функцию
![]() ,
связанную с
,
связанную с![]() соотношением
соотношением
![]() .
.
Дифференцируя
по
![]() и используя правило дифференцирования
сложной функции, находим
и используя правило дифференцирования
сложной функции, находим
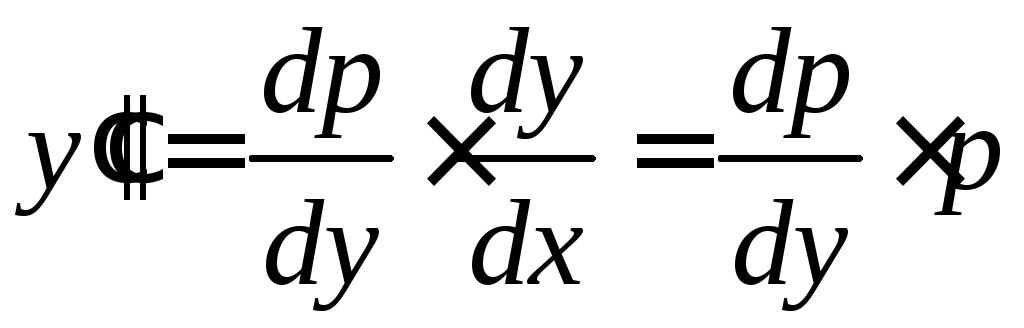 .
.
Подставляя
выражения
![]() и
и![]() в , получим уравнение первого порядка
для функции
в , получим уравнение первого порядка
для функции![]()
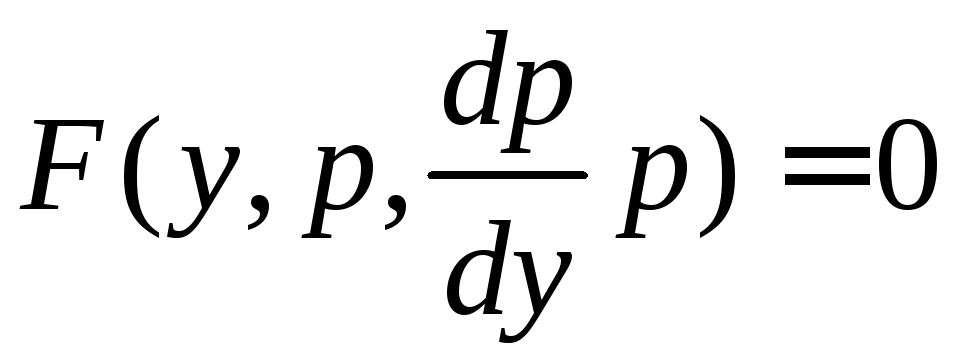 .
.
Пусть
![]() – его общее решение. Общее решение
– его общее решение. Общее решение![]() уравнения находим, решая уравнение
с разделяющимися переменными
уравнения находим, решая уравнение
с разделяющимися переменными
![]() .
.
Аналогично,
уравнение
![]() можно свести к уравнению
можно свести к уравнению![]() -го
порядка для функции
-го
порядка для функции![]() ,
приняв
,
приняв![]() .
.
Примеры решения задач
Решить уравнение
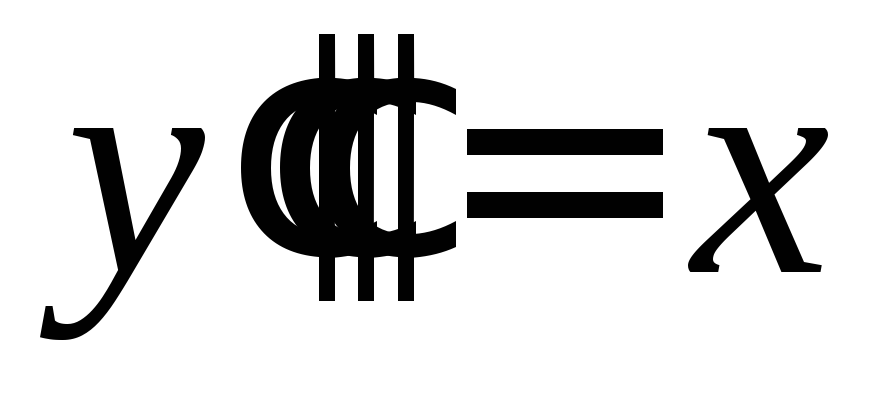 .
.
◄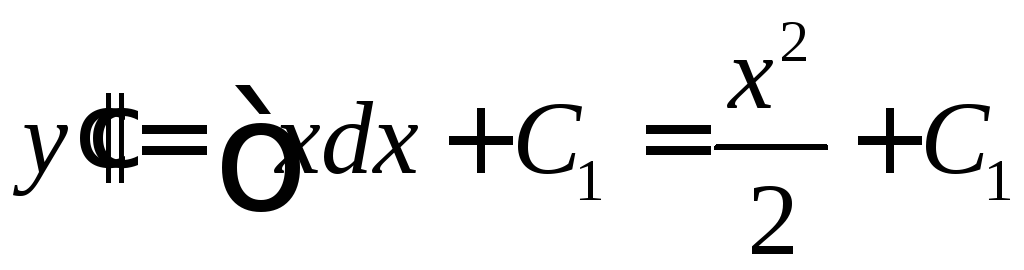 .
.
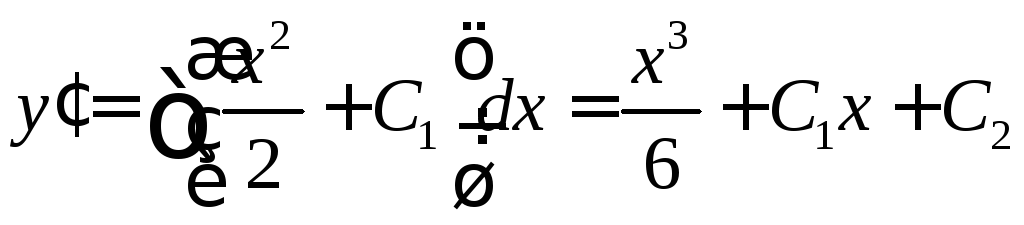 .
.
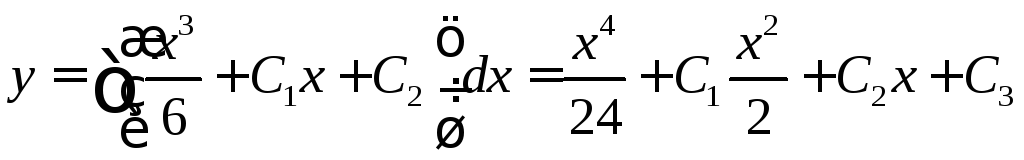 .►
.►
Решить уравнение
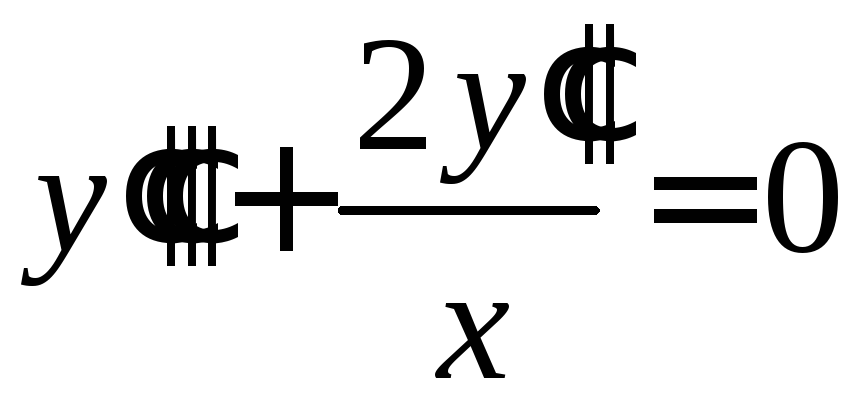 .
.
◄ Уравнение
не содержит явно
![]() и
и![]() .
Делаем замену
.
Делаем замену![]() ,
тогда
,
тогда![]() .
.
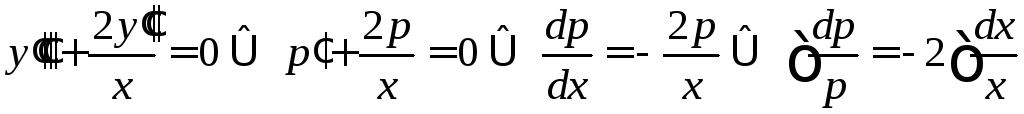 .
.
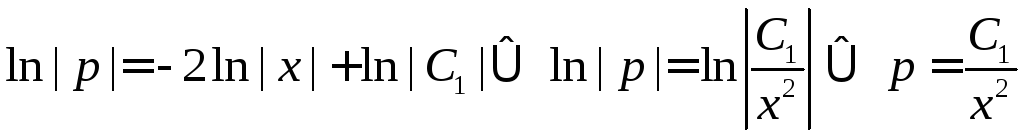 .
.
![]() .►
.►
Замечание.
При решении задачи Коши значения
постоянных
![]() целесообразно находить последовательно
в процессе решения, а не после нахождения
общего решения.
целесообразно находить последовательно
в процессе решения, а не после нахождения
общего решения.
Найти общее решение дифференциального уравнения
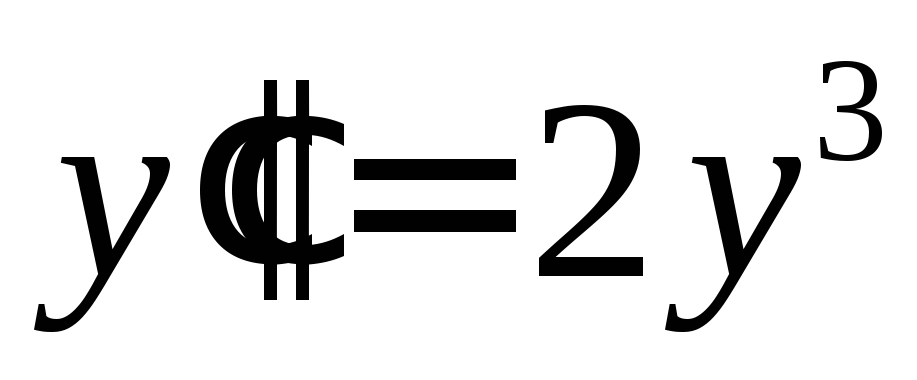 ,
и решение, удовлетворяющее начальным
условиям
,
и решение, удовлетворяющее начальным
условиям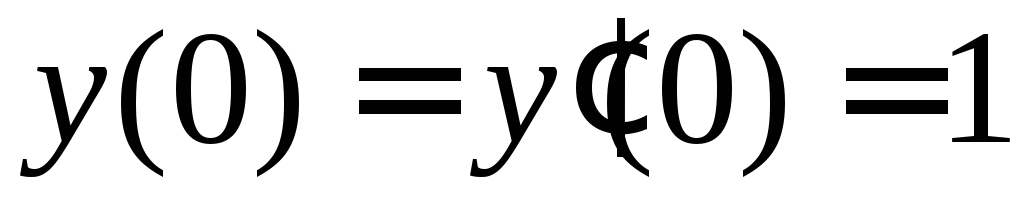 .
.
◄ Уравнение
не содержит явно независимой переменной
![]() .
Делаем замену
.
Делаем замену![]() ,
тогда
,
тогда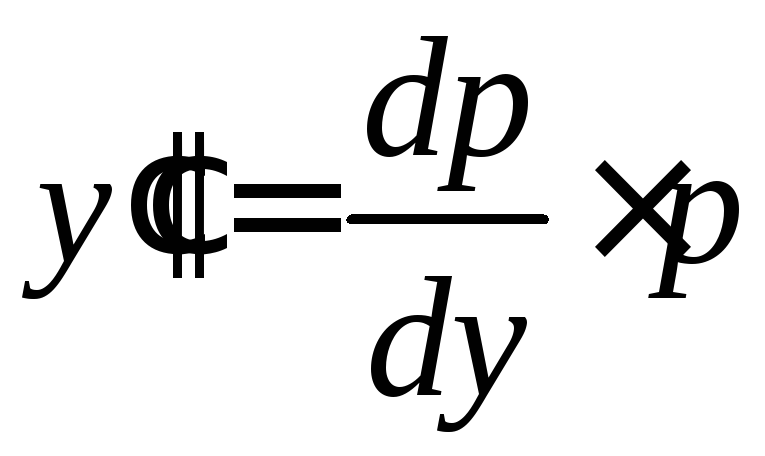 .
Подставив это выражение в уравнение,
получим уравнение с разделяющимися
переменными для функции
.
Подставив это выражение в уравнение,
получим уравнение с разделяющимися
переменными для функции![]() .
.
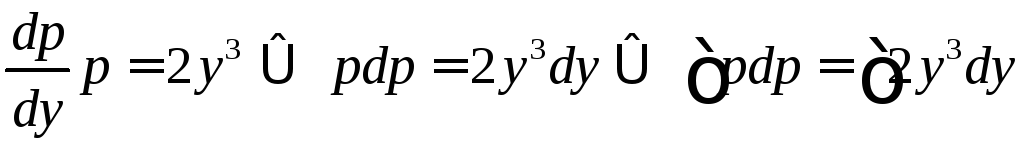
![]()
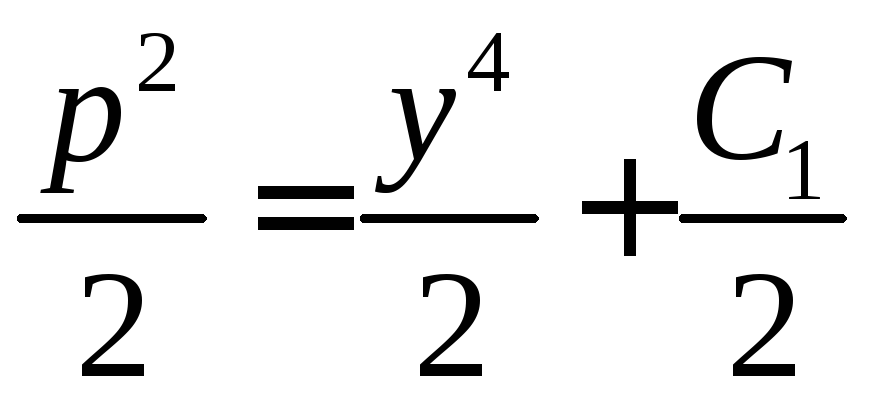 .
.
Таким
образом,
![]() и для функцииy
получаем дифференциальное уравнение
с разделяющимися переменными
и для функцииy
получаем дифференциальное уравнение
с разделяющимися переменными
![]() .
Его общий интеграл имеет вид
.
Его общий интеграл имеет вид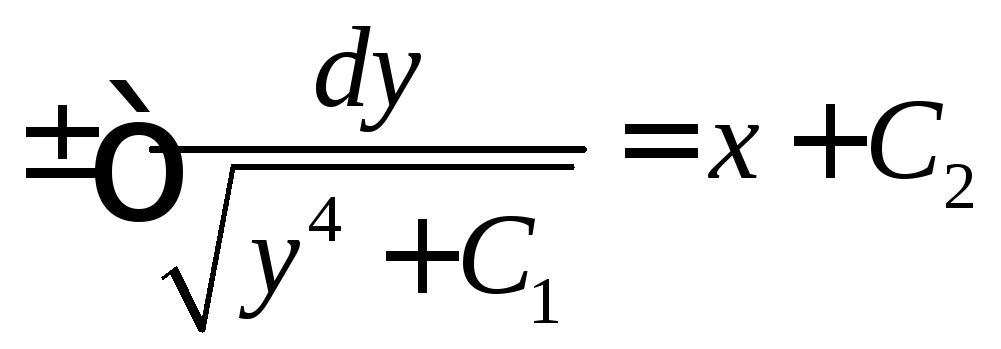 .
Заметим, что левая часть этого уравнения
не выражается через элементарные
функции.
.
Заметим, что левая часть этого уравнения
не выражается через элементарные
функции.
Найдем
теперь решение, удовлетворяющее
начальным условиям
![]() .
Получать его из общего интеграла
неудобно, поэтому вернемся к соотношению
. Подставляя в него
.
Получать его из общего интеграла
неудобно, поэтому вернемся к соотношению
. Подставляя в него![]() ,
получаем
,
получаем![]() .
Теперь
.
Теперь .
Выбираем знак «+», так как
.
Выбираем знак «+», так как![]() .
Для нахождения искомого решения получаем
уравнение
.
Для нахождения искомого решения получаем
уравнение
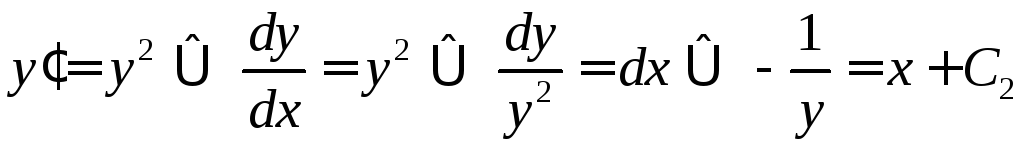 .
.
Подставляя
в полученное соотношение начальные
данные
![]() и
и![]() ,
находим, что
,
находим, что![]() .
В итоге получаем решение задачи Коши
.
В итоге получаем решение задачи Коши
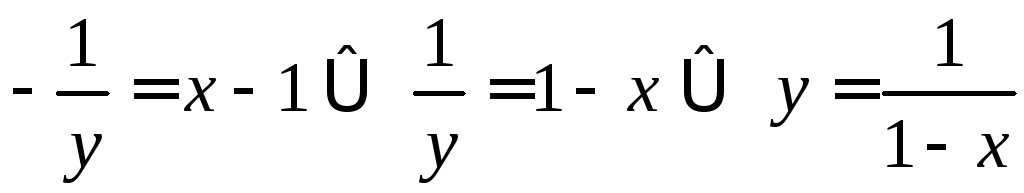 .
.
Приведем
теперь другой вариант решения задачи
Коши, в котором используются определенные
интегралы. Для функции
![]() имеем дифференциальное уравнение
имеем дифференциальное уравнение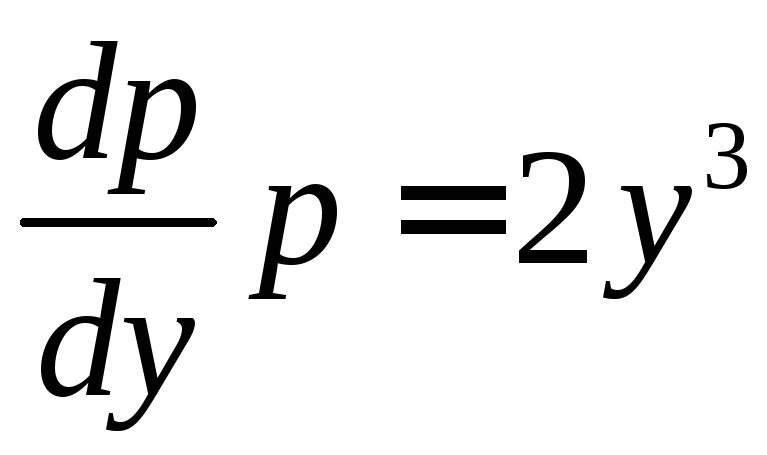 и начальное условие
и начальное условие![]() .
Поэтому
.
Поэтому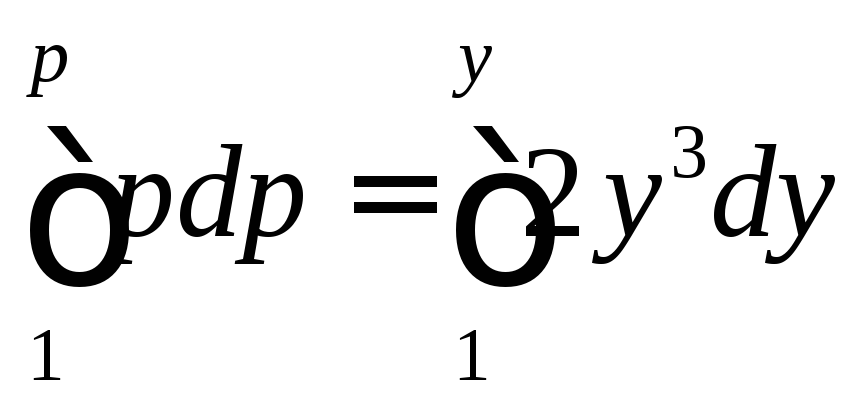 и, следовательно,
и, следовательно,![]() .
Теперь из уравнения
.
Теперь из уравнения![]() и
и
начального
условия
![]() получаем
получаем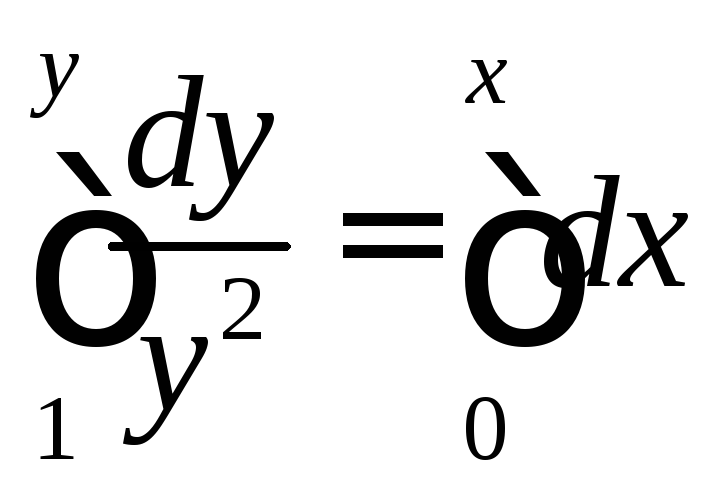
![]()
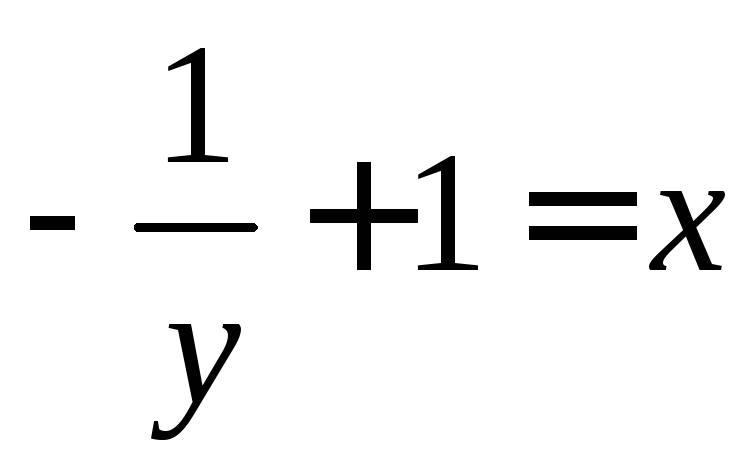
![]()
![]() .►
.►
