2. Примеры решения задач

1. Решить уравнение .

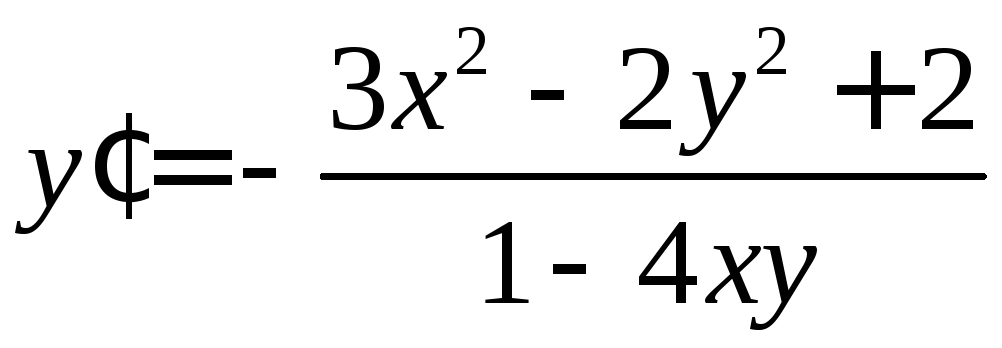◄ Данное уравнение не принадлежит ни к одному из типов, которые мы умеем определять по их нормальной форме. Перепишем исходное уравнение в дифференциальной форме

.

Область определения этого уравнения – односвязна. Проверяем условие .

. .

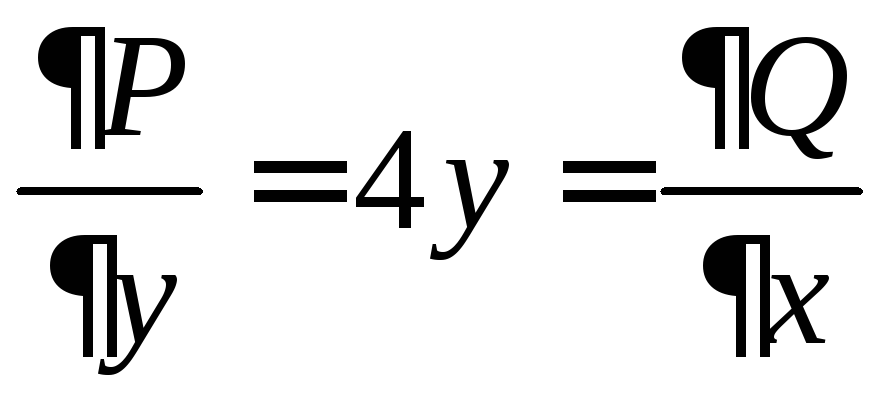Таким образом, мы имеем уравнение в полных дифференциалах. Находим по формуле при

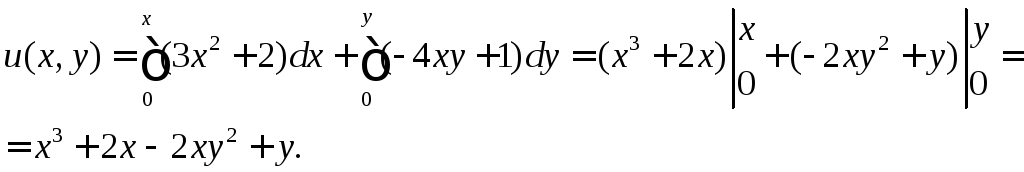
Итак, общий интеграл уравнения имеет вид . ►

3. Задачи для самостоятельного решения

.	.
.	.
.	.

8. Смешанные задачи на дифференциальные уравнения первого порядка

1. Примеры решения задач

1. Для каждого из дифференциальных уравнений

,

,

,

,

,

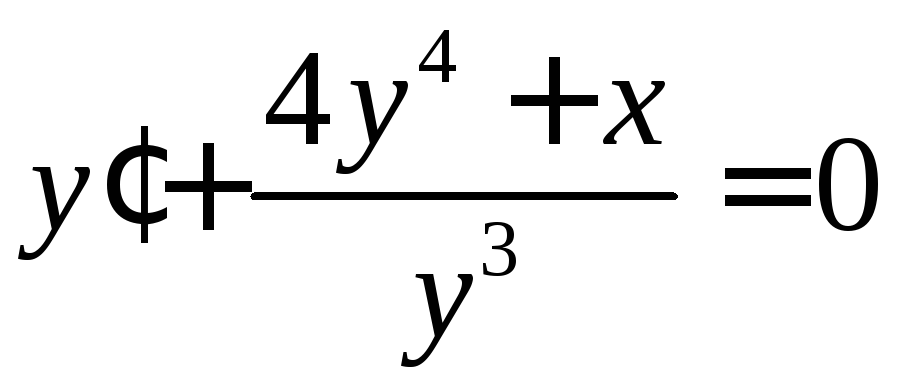определить, является ли оно уравнением одного из следующих типов:

1) уравнением с разделяющимися переменными,

2) однородным уравнением,

3) линейным уравнением,

4) уравнением Бернулли (но не линейным уравнением),

5) уравнением в полных дифференциалах,

6) не является уравнением типов 1) – 5).

◄ Уравнение приведем нормальному виду . В его правую часть переменные входят только в виде отношения, следовательно, – однородное уравнение и его можно решать заменой,. С другой стороны, правая частьявляется линейной функцией переменнойy и уравнение является линейным. Поэтому его можно решать, например, методом Бернулли.

Уравнение имеет нормальный вид. Правую часть можно представить в виде произведения функции от x на функцию от y: , поэтому это уравнение с разделяющими переменными. Поскольку правую часть можно представить в виде, то уравнение является и линейным (линейным неоднородным). Однако нет смысла решать его ни методом Бернулли, ни методом Лагранжа (то есть делать замену переменных, сводящую уравнение к уравнению с разделяющимися переменными) ибо переменные изначально разделяются.

Уравнение записано в дифференциальной форме. Однако уравнением в полных дифференциалах оно не является, так как

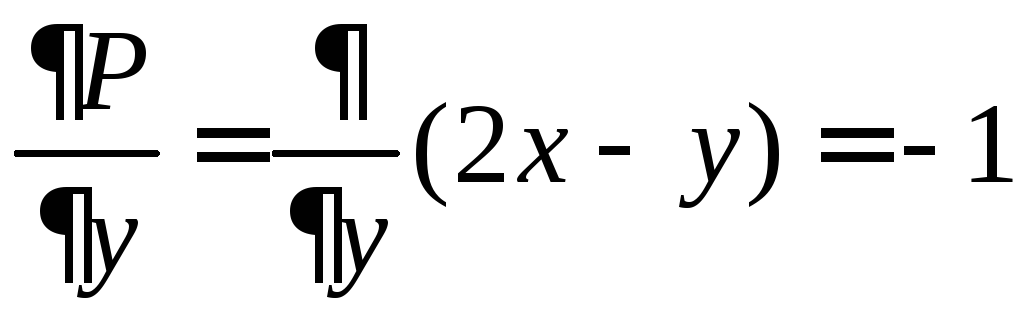, и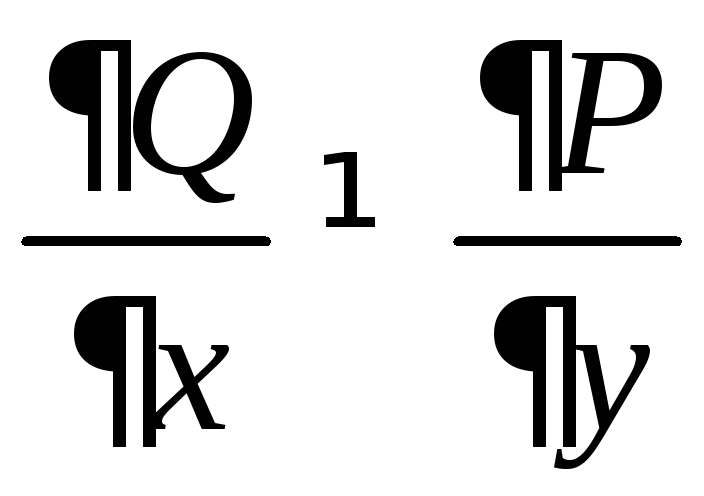. Приведем уравнение (8.3) к нормальному виду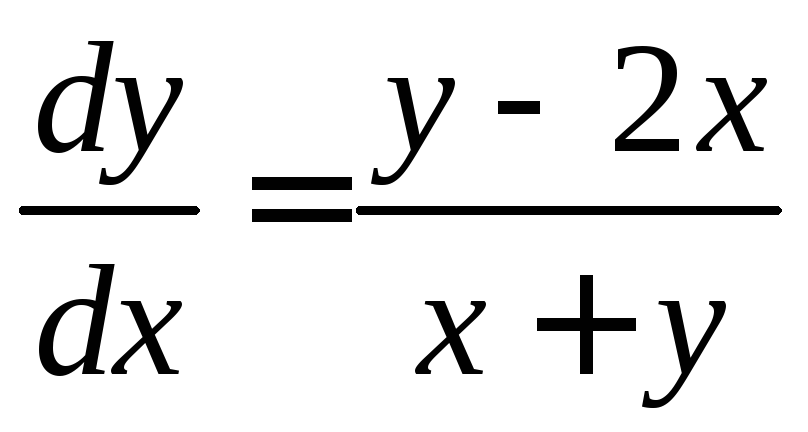. Правая часть является отношением однородных многочленов первой степени. Разделив числитель и знаменатель наx, запишем уравнение в виде 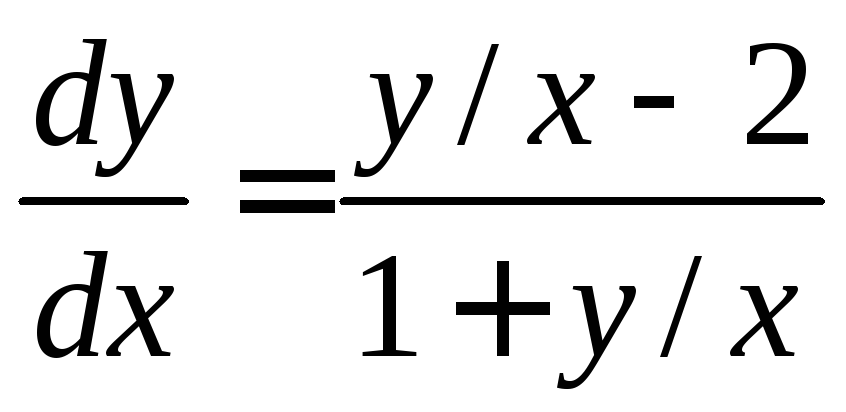, то есть уравнение имеет вид и, следовательно, является однородным.

Уравнение равносильно уравнению , имеющему вид , то есть оно является уравнением Бернулли.

Уравнение является уравнением в полных дифференциалах, так как совпадают производные

и ,

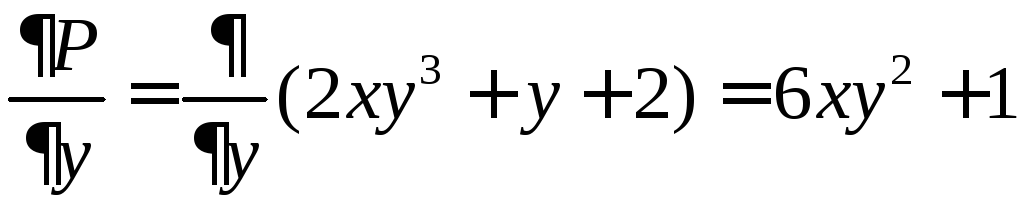а область определения уравнения – односвязна.

Ясно, что уравнение не принадлежит ни одному из типов 1) – 4) (хотя строго доказать это совсем непросто). Записав уравнение в дифференциальной форме , нетрудно убедиться, что условие не выполняется, и потому это уравнение не является уравнением в полных дифференциалах. Итак, для уравнения имеет место случай 6), то есть мы не можем решить уравнение разобранными выше методами. ►
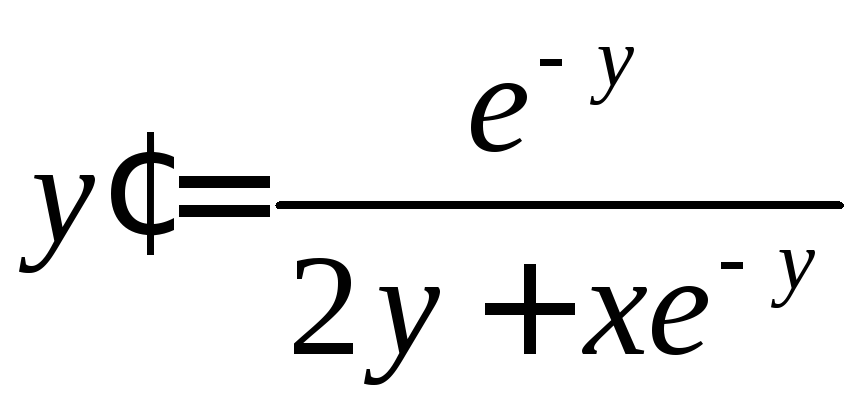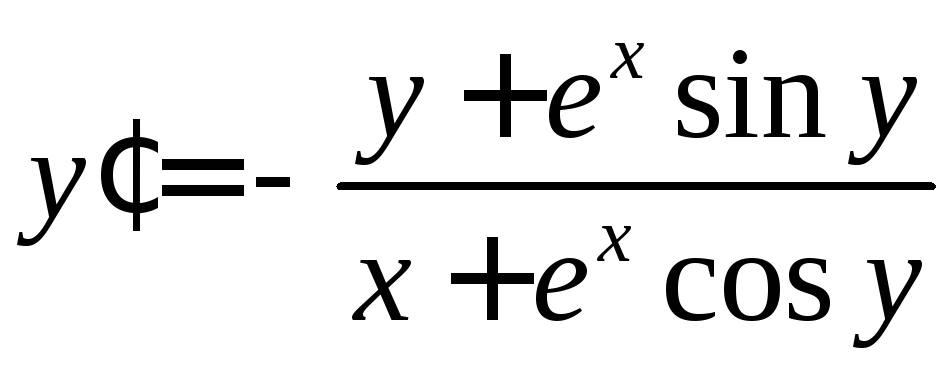