3. Замена переменных в дифференциальных уравнениях первого порядка

1. Сведения из теории

Сделаем в уравнении замену переменных: введем новую неизвестную функцию, связанную с искомой функциейсоотношением, где– дифференцируемая функция. Подставляя выраженияичерезв (3.1), получим для нахожденияуравнение вида, которое при удачном выборе замены может оказаться «проще» первоначального. Например, уравнение

заменой переменной сводится к уравнению с разделяющимися переменными

.

2. Примеры решения задач

1. Решить уравнение .

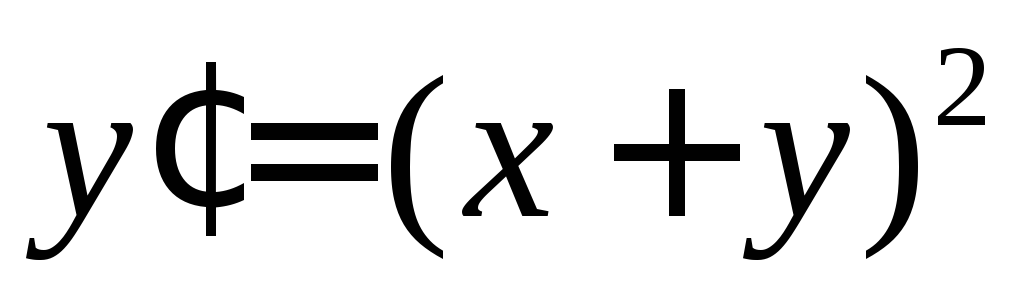◄ Введем новую неизвестную функцию . Выразимичерезz: . Подставим эти выражения в исходное уравнение и решим полученное уравнение с разделяющимися переменными.

.

.

–общее решение уравнения.►

2. Найти решение дифференциального уравнения 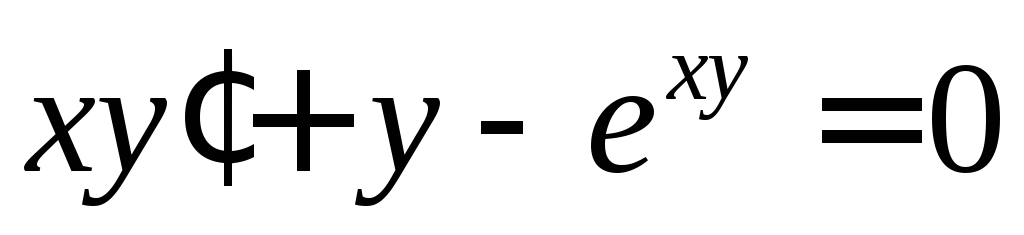, удовлетворяющее начальному условию.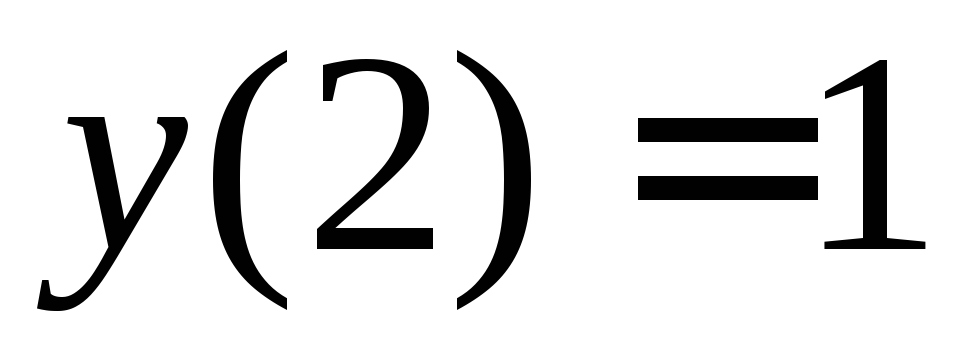

◄ Так как , то естественно сделать замену. Для функцииполучим дифференциальное уравнениес разделяющимися переменными и начальное условие. Разделяем переменные:,, интегрируем: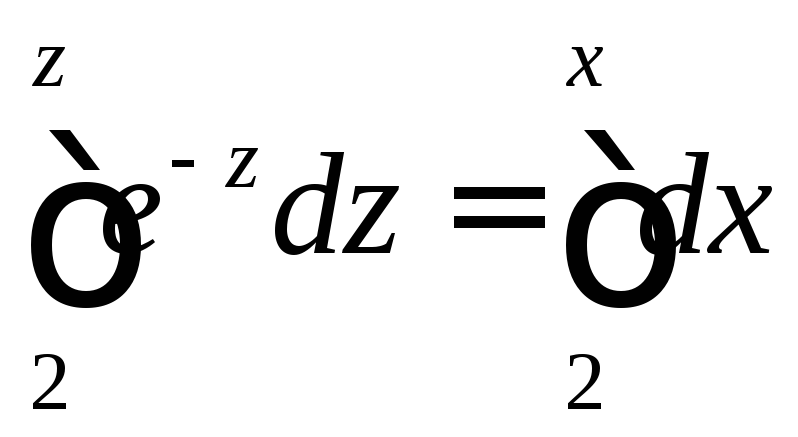, выражаемz, а затем и y через x

, ,,

, ,

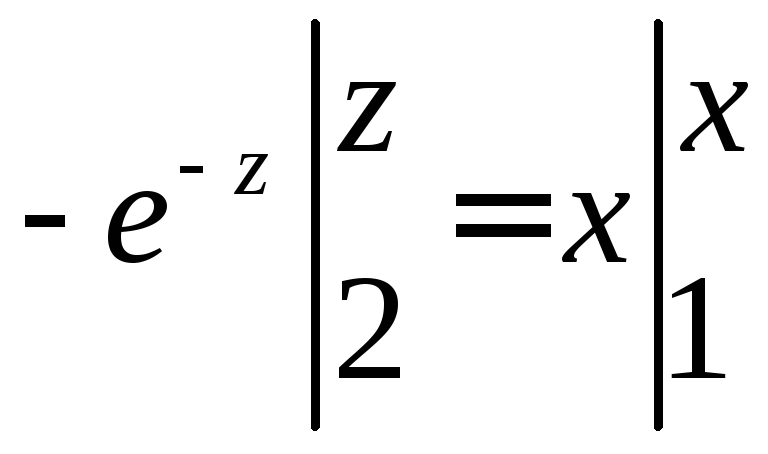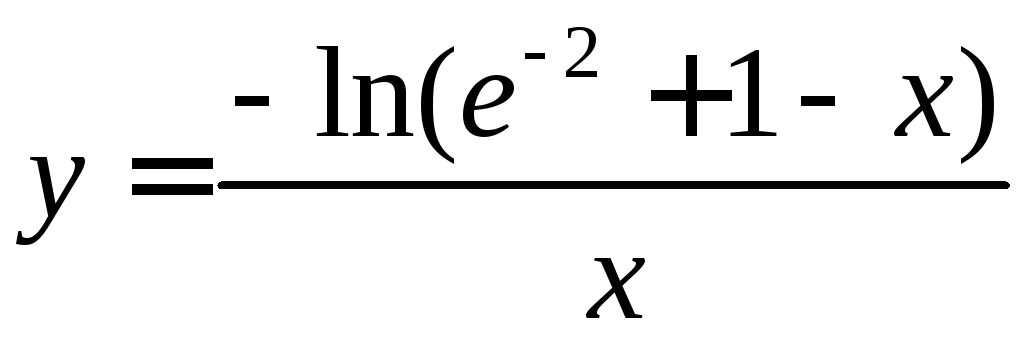–искомое решение.►

3. Задачи для самостоятельного решения

Решить уравнения.

. . Указание: Сделать замену . 3.3.5. . Указание: .

. . Указание: Поскольку , то рекомедуется сделать замену. 3.3.6. . Указание: .

4. Однородные уравнения

1. Сведения из теории

Дифференциальное уравнение, которое можно записать в виде

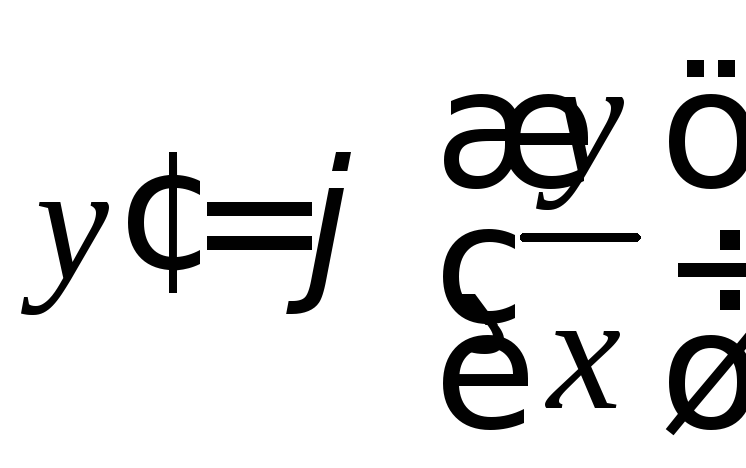
называется однородным. Оно сводится заменой переменной

к уравнению с разделяющимися переменными для функции .

.

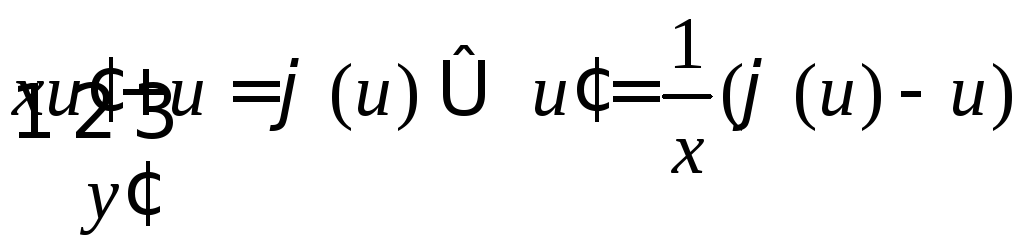Важным примером однородного уравнения является уравнение, правая часть которого – отношение однородных многочленов относительно иодного порядка

.

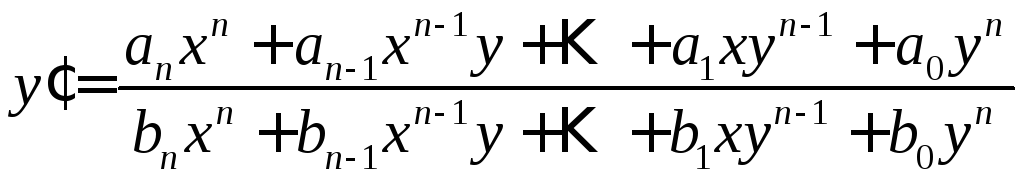Оно приводится к виду , если числитель и знаменатель разделить на .

2. Примеры решения задач

1. Решить уравнение .

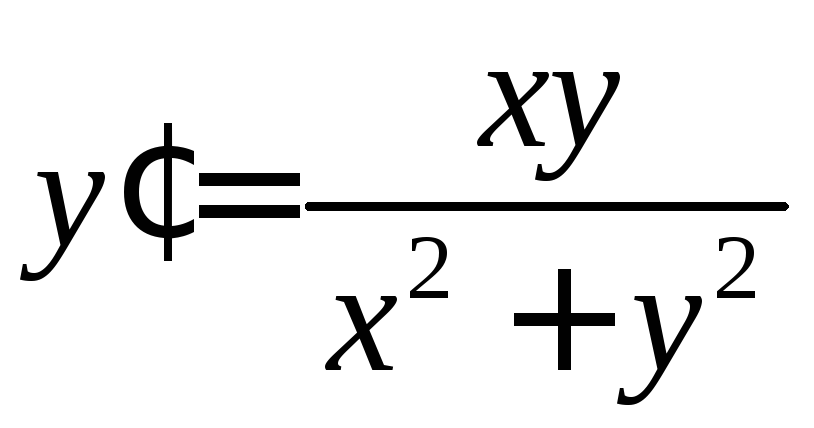◄ Правая часть уравнения – отношение однородных многочленов 2-го порядка. Разделив числитель и знаменатель на , получим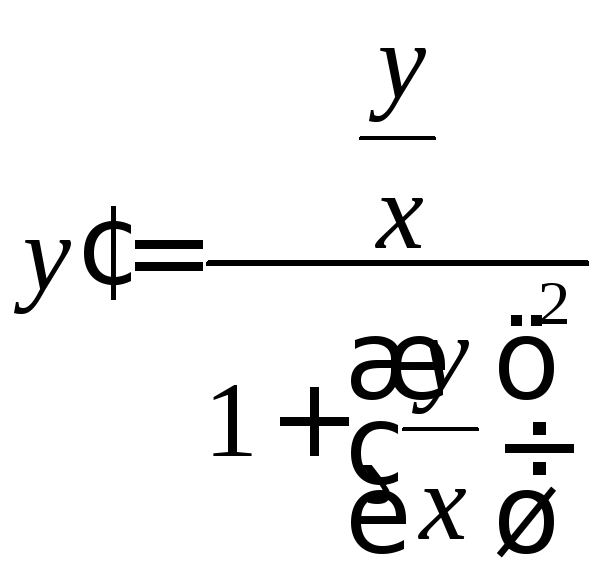

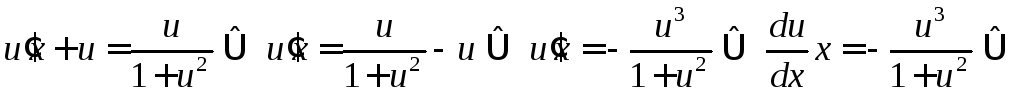
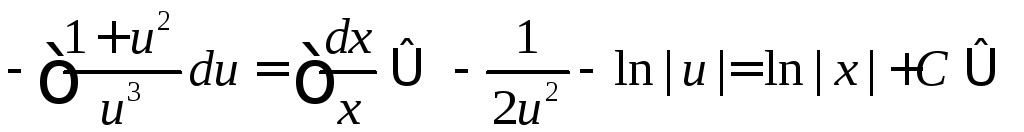
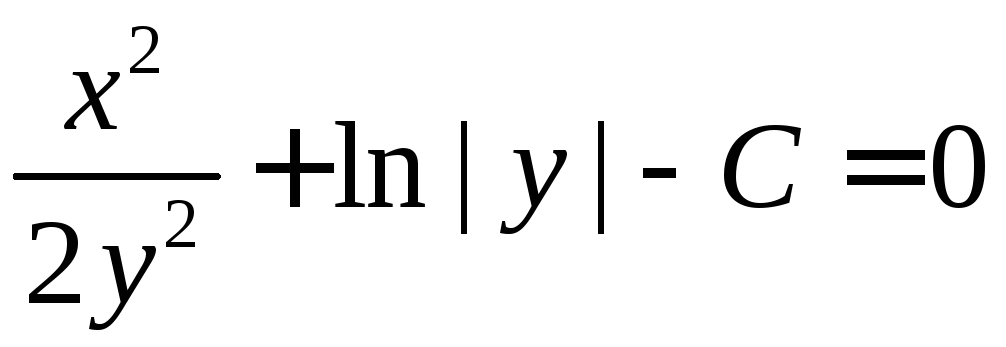
– однородное уравнение. Делаем замену . Тогда,. Для функцииполучаем уравнение с разделяющимися переменными: общий интеграл. ►

2. Найти решение дифференциального уравнения 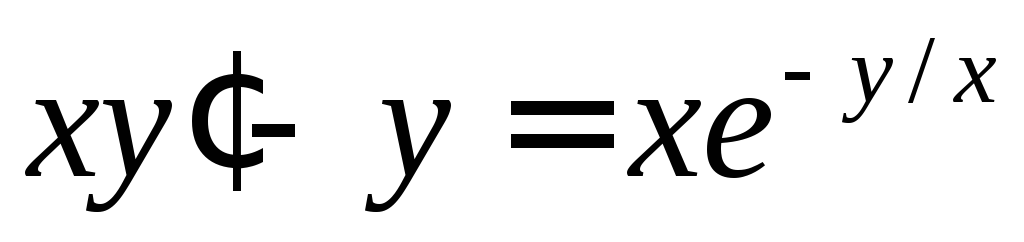, удовлетворяющее условию.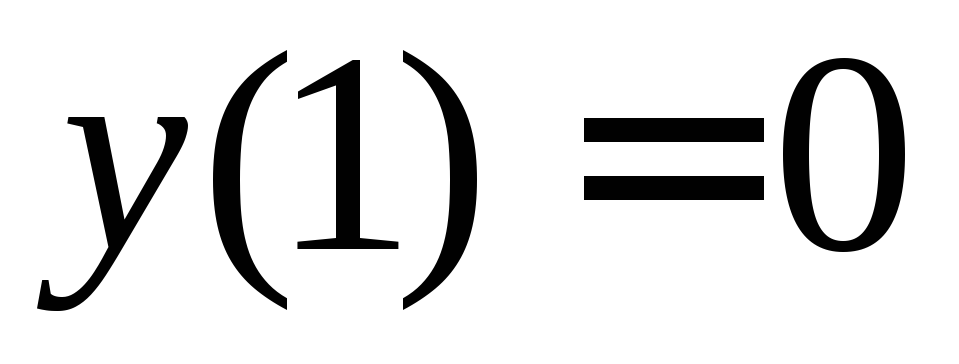

◄ Приведем уравнение к нормальному виду . Так какх и у входят в правую часть только в виде отношения , то это – однородное уравнение. Делаем замену,. Для функцииполучаем уравнениеи начальное условие. Разделяем переменные:,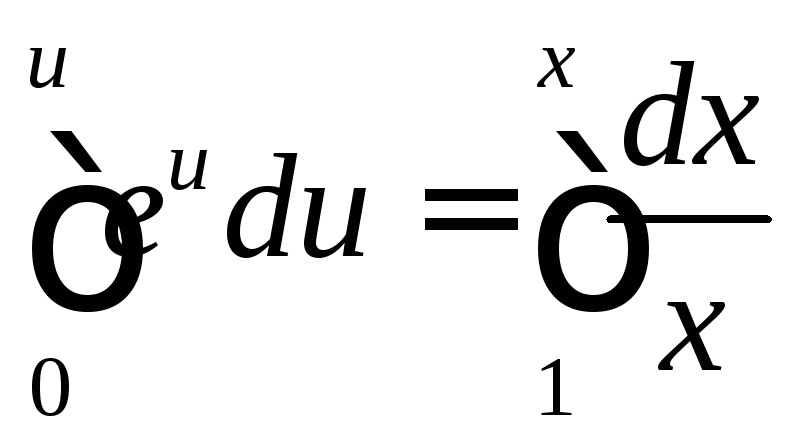;;, и потому– искомое решение.►

3. Задачи для самостоятельного решения

Решить уравнения.

.	.
.	.
. 4.3.7. .	4.3.6. . 4.3.8. .

5. Линейные уравнения первого порядка

1. Сведения из теории

Дифференциальное уравнение первого порядка, разрешенное относительно производной, называется линейным, если его правая часть – линейная функция от

.

При получаемлинейное однородное уравнение

.

Оно является уравнением с разделяющимися переменными, и его общее решение

,

где – одна из первообразных функции. Общее решениелинейного неоднородного уравнения можно найти одним из следующих методов.

1. Метод вариации произвольной постоянной (метод Лагранжа).

Сначала находится общее решение соответствующего линейного однородного уравнения . Решение неоднородного уравнения ищем в виде

,

получающемся из заменой постоянной на функцию. Подставляя в уравнение , получаем для новой неизвестной функцииуравнение. Интегрируя, находим

Подставляя в , получаем общее решение уравнения .

2. Метод Бернулли.

Ищем решение уравнения в виде . Тогда. Подставляя в уравнение , получим . Перепишем это уравнение в виде

.

Подберем так, чтобы скобка в уравнении обратилась в нуль. Для этого нужно найти какое-нибудь частное решениеуравнения с разделяющимися переменными. Подставляяв , получим уравнение с разделяющимися переменными для функции

.

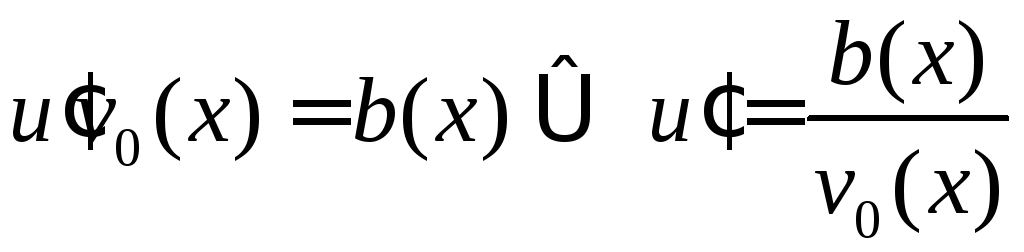Интегрируя, находим его общее решение . Перемножая найденные значенияи, получим общее решение неоднородного уравнения.
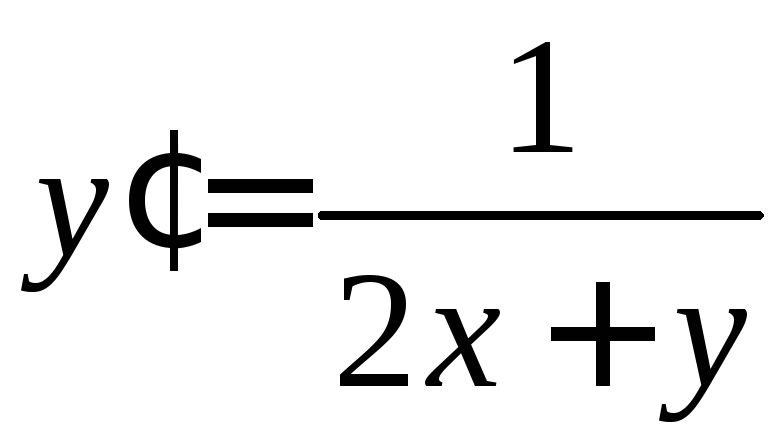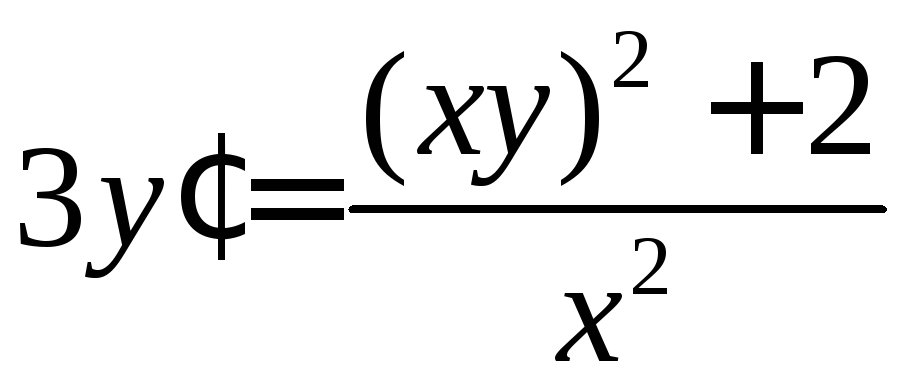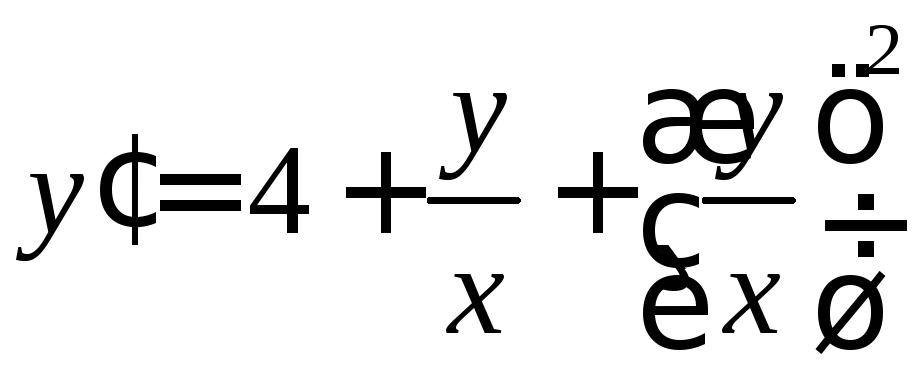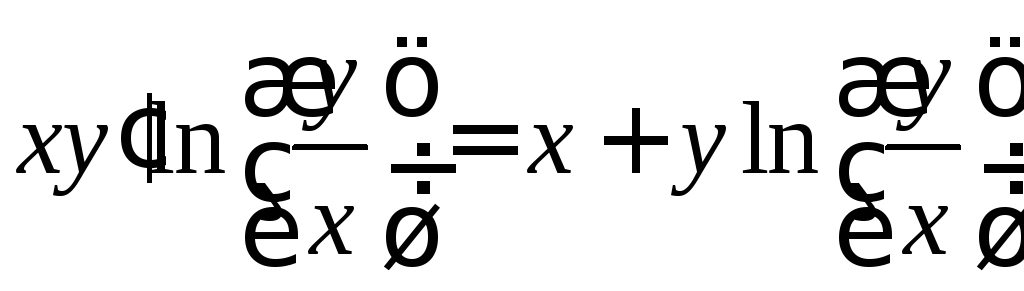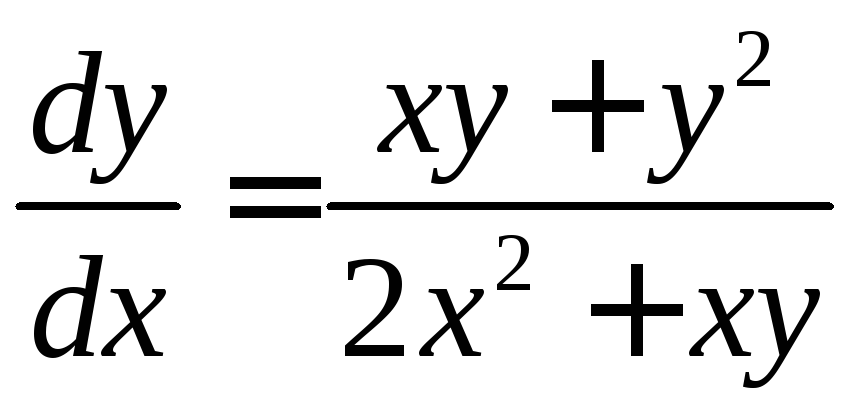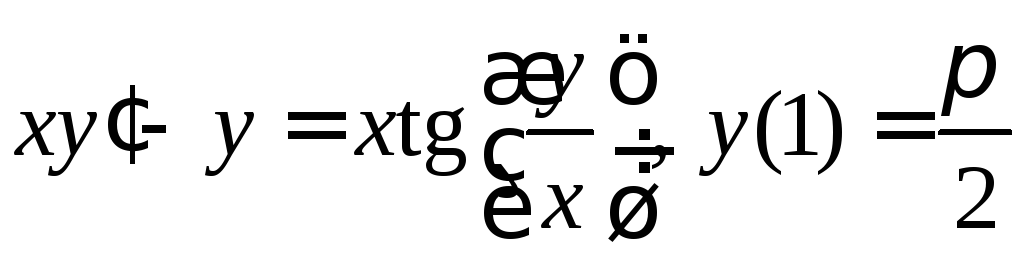