Список литературы
Бугров, Я.С. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я.С. Бугров, С.М. Никольский. – М. : Наука, 1985. – 464с.
Пискунов, П.С. Дифференциальное и интегральное исчисление для втузов». Т. 2, 13 изд., М. : Наука, 1985. -560 с.
Сборник задач по высшей математике для вузов. Ч.2. Специальные разделы математического анализа. / Под ред. А.В. Ефимова, Б.П. Демидовича. – М. : Наука, 1986. – 366 с.
Данко, П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – 5-е изд., исп. – М. : Высшая школа, 1999. – 304 с.
Филиппов, А.Ф. Сборник задач по дифференциальным уравнениям М., Наука, 1985. – 128 с.
Краснов, М.Л. Сборник задач по дифференциальным уравнениям / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. - М. : Высшая школа, 1978, - 388с.
Карташов, А.П. Обыкновенные дифференциальные уравнения и основы вариационного исчисления / А.П. Карташов, Б.Л. Рождественский. – М.: Наука, 1980. – 287 с.
Самойленко, А.М. Дифференциальные уравнения: Примеры и задачи / А.М. Самойленко, С.А. Кривошея, Н.А. Перестюк. – 2-е изд., перераб. – М. : Высшая школа, - 1989. – 383 с.
http://www. krelib.com [Электронный ресурс].
Ответы
2.3.2.
.
2.3.4.
.
2.3.6.
.
2.3.8.
.
2.3.10.
.
2.3.12.
.
2.3.14.
.
2.3.16.
.
2.3.17.
60
мин. 2.3.19.
18,4
мин.
3.3.2.
.
3.3.4.
.
3.3.6.
.
4.3.2.
.
4.3.4.
.
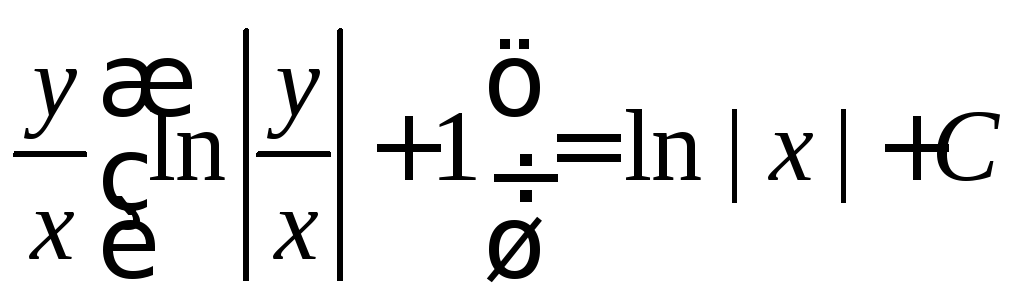4.3.6.
.
4.3.8.
.
5.3.2.
.
5.3.4.
.
5.3.6.
.
5.3.8.
.
5.3.9. А); б).
6.3.3.
.
6.3.4.
.
7.3.2.
.
7.3.4.
.
7.3.6.
.
8.2.2.
.
8.2.4.
.
8.2.6.
.
8.2.8.
.
8.2.10.
.
8.2.12. НЛДУ1. 8.2.14. ОЛДУ1. 8.2.16. с разделяющимися переменными.
8.2.18. однородное. 8.2.20. уравнение Бернулли.
9.3.1.
а)
;
б)
.
10.3.2.
.
10.3.4.
.
10.3.6.
.
10.3.8.
.
10.3.10.
.
10.3.12.
.
10.3.14.
.
11.3.1.
.
11.3.2.
.
12.3.2.
.
12.3.4.
.
12.3.6.
.
12.3.8.
.
12.3.10.
.
12.3.12.
.
12.3.14.
.
13.3.2.
.
13.3.4.
.
13.3.6.
.
13.3.8.
.
13.3.10.
.
13.3.12.
.
13.3.14.
.
13.3.16.
.
13.3.18.
.
13.3.20.
.
13.3.22.
.
14.3.2.
.
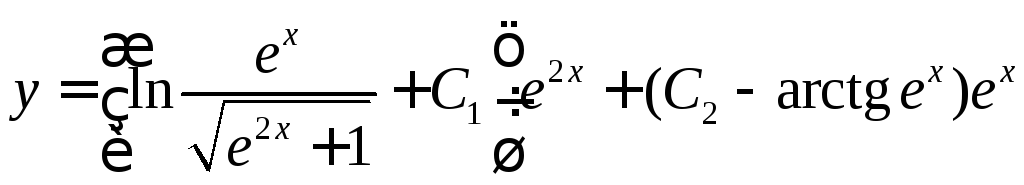14.3.4.
.
14.3.6.
.
Задания для РГР
Задания 1-15 – решить данные дифференциальные уравнения.
Задание
16 – по данным корням характеристического
уравнения некоторого линейного
однородного дифференциальные уравнения,
найти это дифференциальное уравнение
и записать его общее решение. Для
соответствующего неоднородного
уравнения с данной функцией
в правой части записать общий вид
частного решения неоднородного
уравнения.
Задание 17 .
А) решить данную систему дифференциальных уравнений.
Б)
Исследовать положение равновесия
на устойчивость.
В) Определить тип положения равновесия и изобразить фазовый портрет.
Задание 18 .
А)
Убедиться, что
- положение равновесия.
Б) Исследовать на устойчивость положение равновесия по первому приближению.
В)
Определить тип положения равновесия
в окрестности точки
.