3. Задачи для самостоятельного решения

Решить уравнения.

.	.
.	.
.	.
.	.
.	.
. .	.
.	.
.	.

Найти вид частного решения.

.	.
.	.

14. Линейные неоднородные дифференциальные уравнения n-го порядка. Метод вариации произвольных постоянных

1. Сведения из теории

Метод вариации произвольных постоянных (метод Лагранжа) решения линейного неоднородного уравнения

состоит в следующем.

Пусть известна фундаментальная система решений

соответствующего линейного однородного уравнения

.

Общее решение неоднородного уравнения ищется в виде

,

получающемся из общего решения однородного уравнения заменой произвольных постоянных на функции. Производныеэтих функций находятся из системы линейных алгебраических уравнений

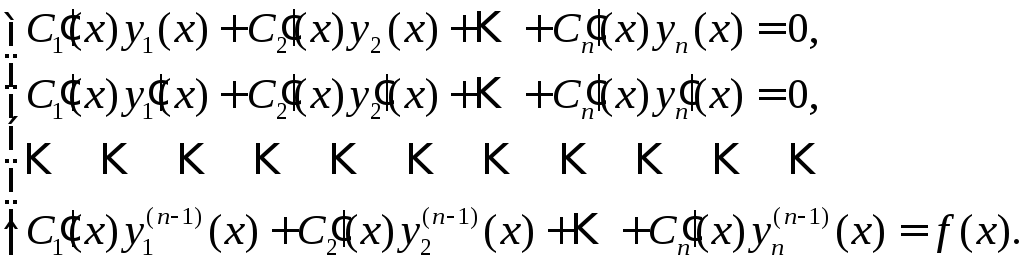
Определитель этой системы – определитель Вронского – линейно независимой системы функцийотличен от нуля, а система имеет единственное решение

.

Интегрируя, находим:

, , …, ,

где – произвольные постоянные.

Подставляя найденные в , получим общее решение уравнения .

2. Примеры решения задач

1. Решить уравнение .

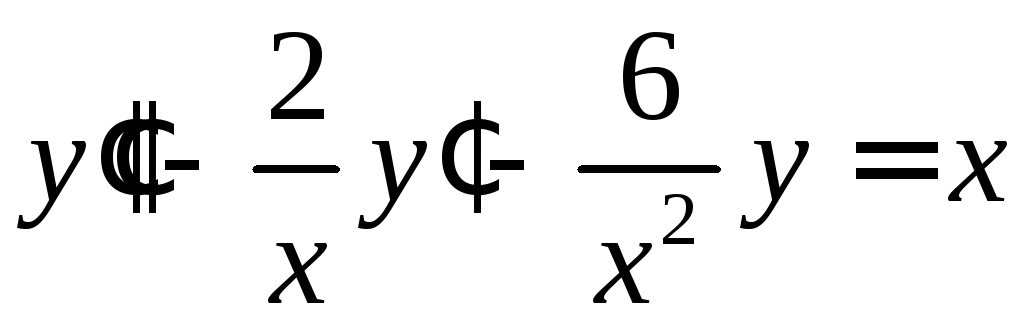◄Соответствующее однородное уравнение имеет переменные коэффициенты и не может быть решено методом, описанным в п.12. Его ф.с.р. указана в задаче 11.3.1:,. Общее решение неоднородного уравнения ищем в виде

.

Производные инаходятся из системы линейных алгебраических уравнений , имеющей привид

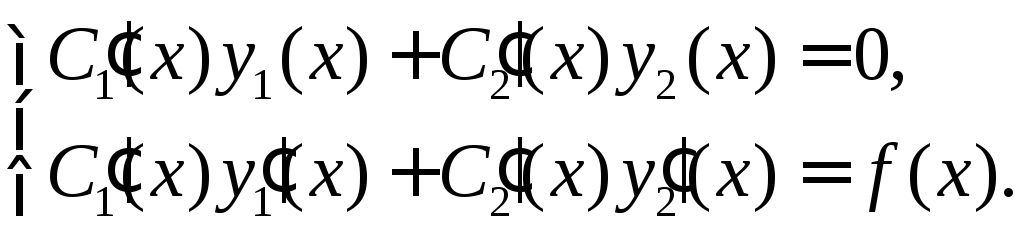
Для нашего уравнения это будет система

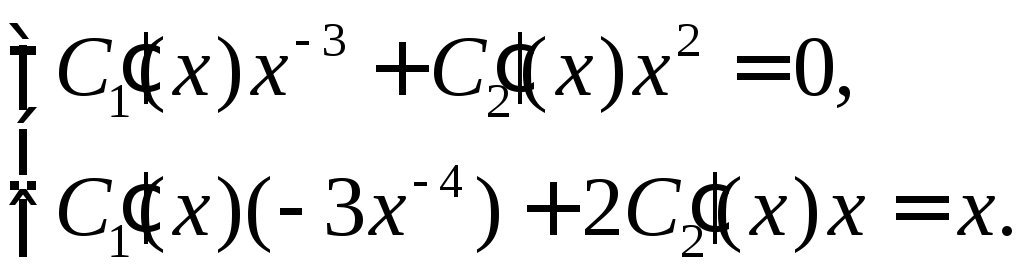
Решаем ее по формулам Крамера.

,

,

,

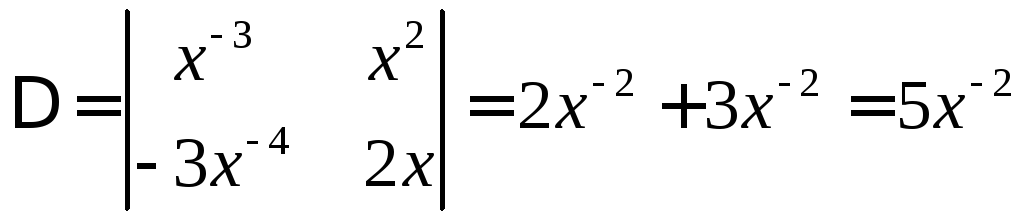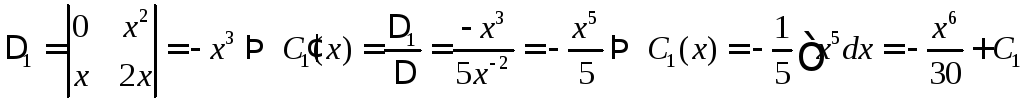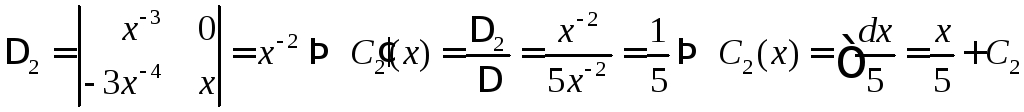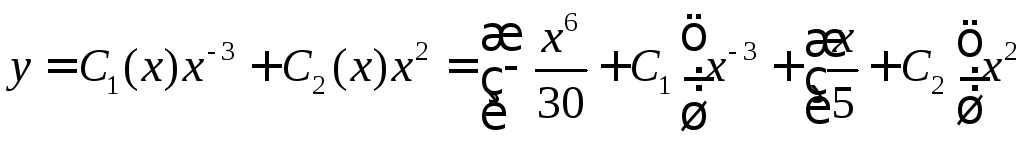или 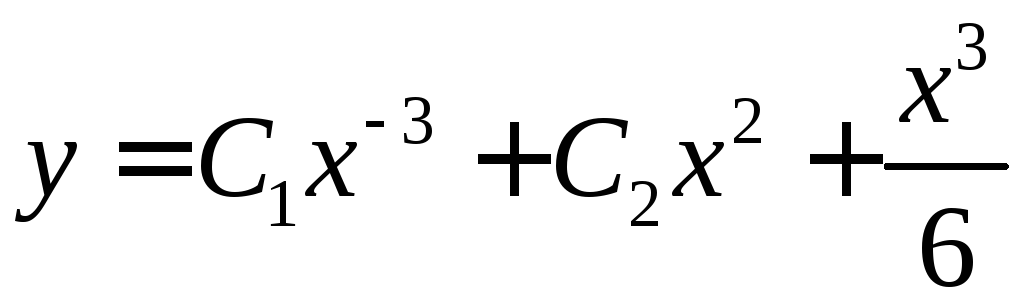– общее решение.►

2. Решить уравнение .

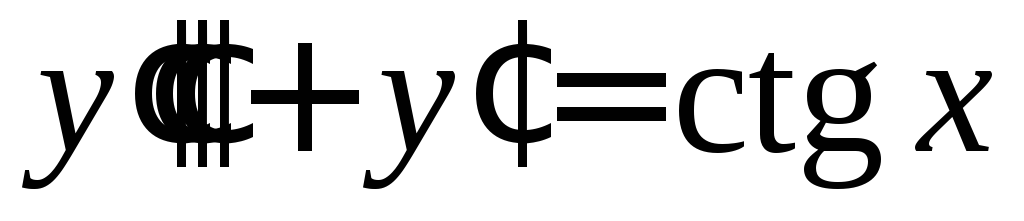◄ Соответствующее однородное уравнение имеет постоянные коэффициенты. Его характеристическое уравнение имеет корни,. Им в ф.с.р. соответствуют решения. Общее решение уравнения ищем в виде

.

Система для этого уравнения имеет вид

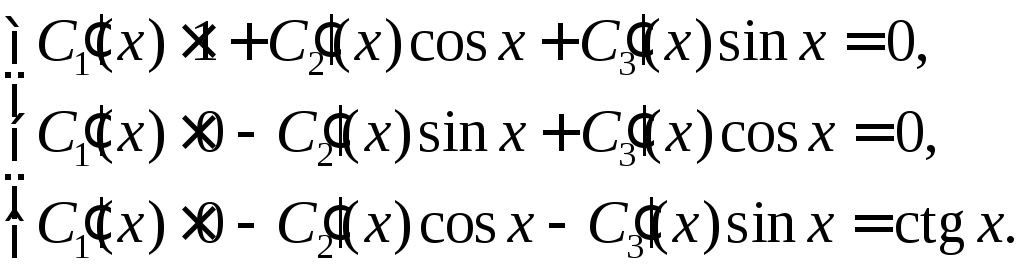
Ее можно решать по формулам Крамера, но удобнее воспользоваться спецификой системы. Складывая первое и третье уравнение, получаем ,

Умножая второе уравнение на , третье – на () и складывая их получим.

Из второго уравнения

.

.

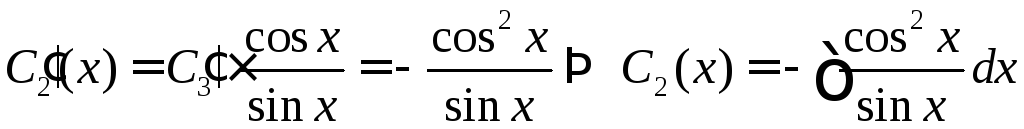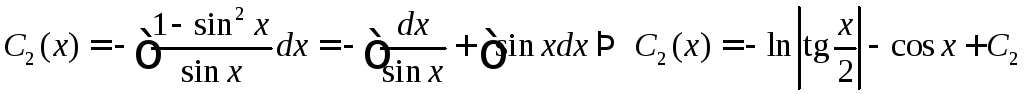Подставляя ,ив , получаем общее решение

.►

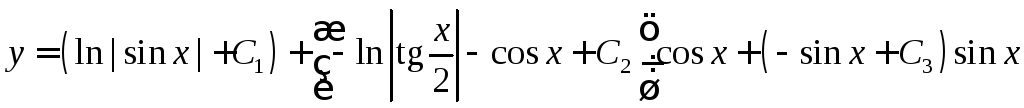3. Задачи для самостоятельного решения

Решить уравнения.

.	.
.	.
.	.
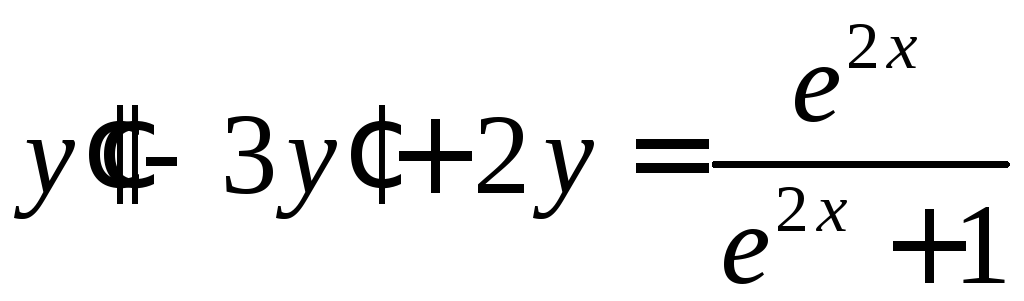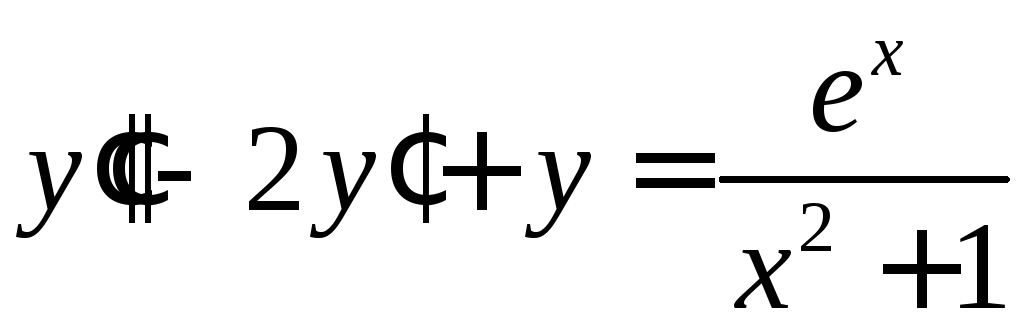