2. Примеры решения задач

1. Решить уравнение .

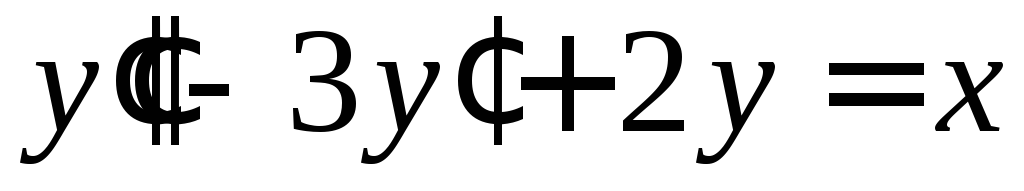◄ Это линейное неоднородное уравнение 2-го порядка с постоянными коэффициентами. Соответствующее линейное однородное уравнение: . Его характеристическое уравнениеимеет корни, а ф.с.р. состоит из функций

.

Правая часть неоднородного уравнения – многочлен 1-й степени, частный случай правой части вида с (п.1 таблицы). Так как, тои, согласно таблице, решениенадо искать в виде многочлена 1-й степени:. Подставляя,ив исходное уравнение, получим

.

Приравниваем коэффициенты при одинаковых степенях в левой и правой частях, найдем. Таким образом,.

Общее решение имеет вид ,.►

2. Решить уравнение .

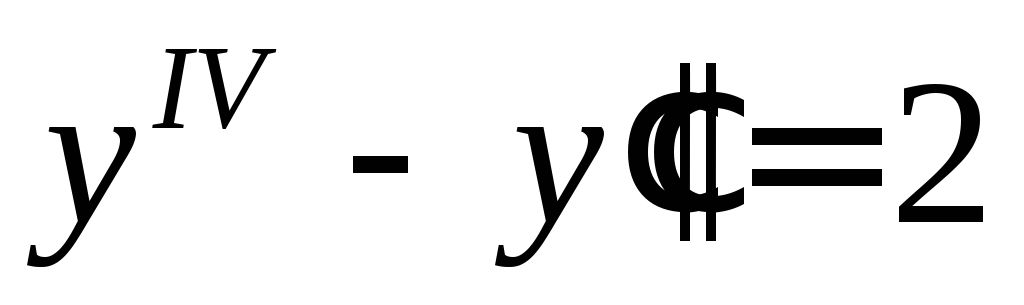◄ Соответствующее характеристическое уравнение имеет корни,,, которым в фундаментальной системе решений однородного уравнения отвечают решения

, ,.

Правая часть уравнения постоянная, то есть многочлен нулевой степени; число – совпадает с двукратным корнем, то есть. Согласно п.1 таблицы решениеищем в виде. Вычисляем,,и поставляем в исходное уравнение. Получим,.

–общее решение. ►

3. Решить уравнение .

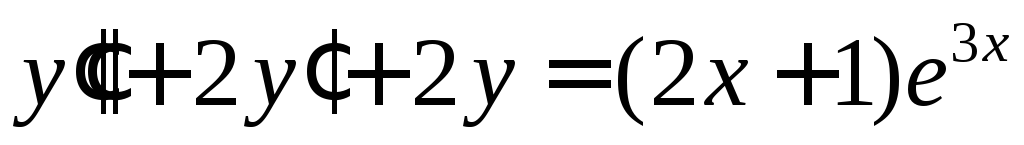◄ Характеристическое уравнение имеет корни. Ф.с.р. однородного уравнения. Согласно п. 2 таблицы,, и частное решение неоднородного уравнения ищем в виде. Вычислим его производные и подставим в уравнение, оформив эти процедуры в виде следующей схемы

2
2
1

Приравниваем коэффициенты при одинаковых степенях в левой и правой частях, и решаем полученную систему уравнений.

.

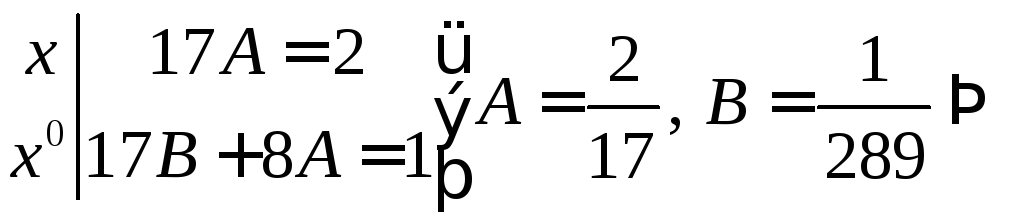
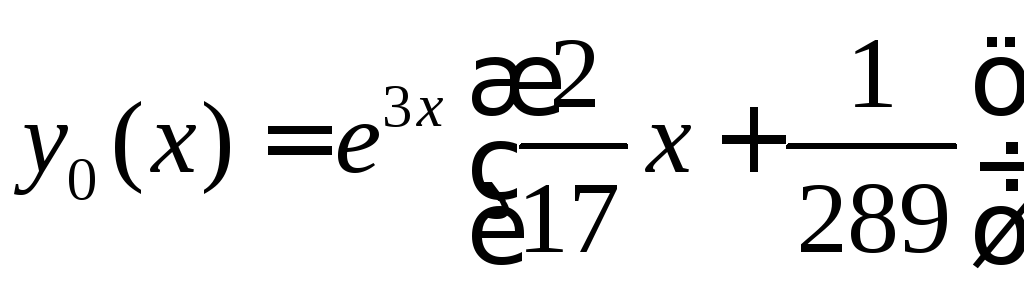Общее решение . ►

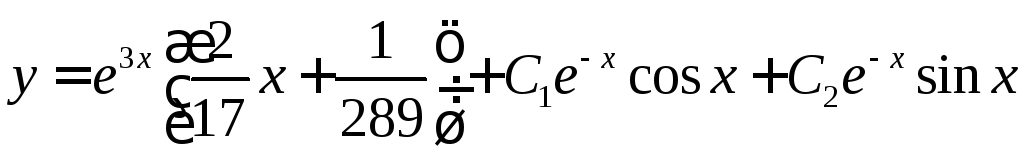4. Решить уравнение .

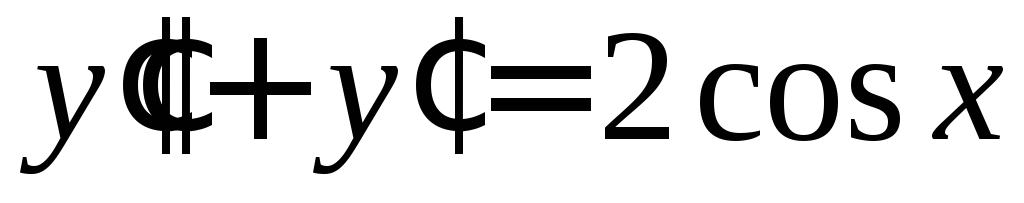◄ Характеристическое уравнение имеет корни,. Ф.с.р. однородного уравнения,. Согласно п. 3 таблицы:,.

0
1
1

Приравнивая коэффициенты при ив левой и правой частях этого равенства, получаем.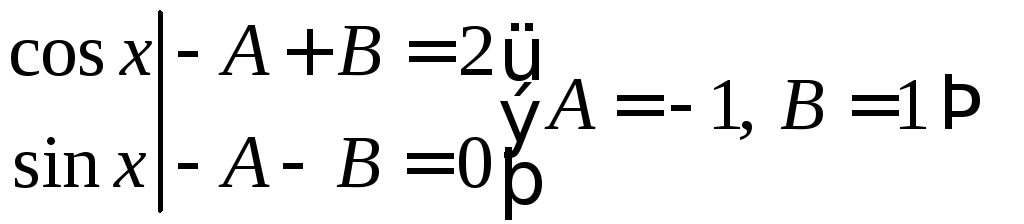

Общее решение .►

5. Решить уравнение .

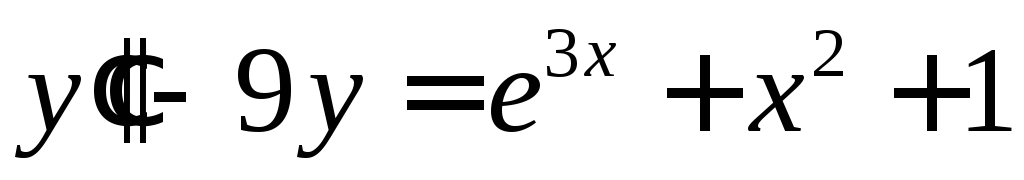◄ Характеристическое уравнение имеет корни. Ф.с.р. однородного уравнения,. Правая часть неоднородного уравнения представляет собой сумму двух функцийивида . Согласно п. 2 таблицы для первого слагаемого,, и частное решение неоднородного уравнения с правой частьюимеет вид. Согласно п. 1 таблицы для второго слагаемого,, и частное решение неоднородного уравнения с правой частьюимеет вид. Частное решение неоднородного уравнения ищем в виде суммы двух слагаемых. Вычисляем производные и подставляем уравнение

–9 0 1

Полученное равенство будет верно, если

, .

Отсюда ,

	, ,
	, ,
	, .

Таким образом, , а общее решение имеет вид. ►

6. Найти вид частного решения уравнения

.

◄ Корни характеристического уравнения . Правая часть – сумма двух слагаемых стандартного вида:и. Соответствующие им числа;. Частное решениеищем в виде суммы двух слагаемых.►