
- •Кафедра высшей математики
- •Обыкновенные дифференциальные уравнения
- •Дифференциальные уравнения первого порядка. Общие понятия
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Уравнения с разделяющимися переменными
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Замена переменных в дифференциальных уравнениях первого порядка
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Однородные уравнения
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные уравнения первого порядка
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Смешанные задачи на дифференциальные уравнения первого порядка
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Дифференциальные уравнения высших порядков
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Линейные однородные дифференциальные уравнения n-го порядка
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные однородные уравнения с постоянными коэффициентами
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные неоднородные дифференциальные уравнения n-го порядка. Метод неопределенных коэффициентов
- •Сведения из теории
- •И соответствующие им частные решения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные неоднородные дифференциальные уравнения n-го порядка. Метод вариации произвольных постоянных
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Список литературы
- •5.3.9. А); б).
- •Вариант 1
- •150023, Ярославль, Московский пр., 88
Федеральное агентство по образованию
Государственное образовательное учреждение
«Ярославский государственный технический университет»
Кафедра высшей математики
Рекомендовано
научно-методическим советом
инженерно-экономического
факультета
Обыкновенные дифференциальные уравнения
Методические указания и расчетно-графические задания
для студентов очного отделения
Ярославль
2007
УДК 517(07)
МУ 54-07. Обыкновенные дифференциальные уравнения: Метод. указания и расчетно-графические задания для студентов очного отделения / Сост.: Б.И. Бутрим, В.А. Короткий, В.Ш. Ройтенберг, Л.А. Сидорова, – 2-е изд., испр. и доп. - Ярославль : Изд-во ЯГТУ, 2007. – 72 с.
Содержат краткие теоретические сведения по разделу «Дифференциальные уравнения», подробно разобранные типовые задачи, а также 30 вариантов расчетно-графических заданий.
Предназначены для студентов 2-го курса всех специальностей очного отделения. Могут быть полезны при подготовке контрольных работ и выполнении домашних заданий.
Ил. 1. Библиогр. 9.
Рецензенты: кафедра высшей математики Ярославского государственного технического университета;
Д.В. Садовников, канд. физ.-мат. наук, зав. кафедрой естественно-научных и математических дисциплин ЯФМАП.
Ярославский государственный технический университет, 1993
Ярославский государственный технический университет, 2007, с изменениями
Дифференциальные уравнения первого порядка. Общие понятия
Сведения из теории
Обыкновенным дифференциальным уравнением первого порядка называется функциональное уравнение вида
![]() или
коротко
или
коротко
![]() ,
,
связывающее
независимую переменную
![]() ,
неизвестную функцию
,
неизвестную функцию![]() и ее производную первого порядка
и ее производную первого порядка![]() .
.
Решением
(частным
решением)
уравнения
называется функция
![]() ,
которая, будучи подставленной в уравнение,
обращает его в тождество
,
которая, будучи подставленной в уравнение,
обращает его в тождество![]() .
График решения называетсяинтегральной
кривой.
.
График решения называетсяинтегральной
кривой.
Будем рассматривать только такие уравнения, которые можно представить в нормальной форме – разрешить относительно производной
![]() .
.
Задача
Коши для
уравнения состоит в том, что ищется
решение
![]() ,
,![]() ,
уравнения, удовлетворяющееначальному
условию
,
уравнения, удовлетворяющееначальному
условию
![]() ,
,
где
![]() – заданная пара чисел. Геометрически
это означает, что ищется интегральная
кривая, проходящая через точку
– заданная пара чисел. Геометрически
это означает, что ищется интегральная
кривая, проходящая через точку![]() .
.
Справедлива
теорема
существования и единственности:
если функция
![]() в некоторой окрестности точки
в некоторой окрестности точки![]() непрерывна и имеет непрерывную частную
производную
непрерывна и имеет непрерывную частную
производную![]() ,
то найдется промежуток
,
то найдется промежуток![]() ,
на котором задача Коши - имеет и притом
единственное решение
,
на котором задача Коши - имеет и притом
единственное решение![]() .
.
Общим
решением
уравнения (1.2) в области
![]() называется семейство
называется семейство![]() функций аргумента
функций аргумента![]() ,
зависящих от параметра
,
зависящих от параметра![]() (называемого произвольной постоянной)
такое, что
(называемого произвольной постоянной)
такое, что
1)
при фиксированных значениях параметра
С функции
![]() – решения уравнения, при этом
– решения уравнения, при этом![]() ;
;
2)
![]() можно подобрать значение
можно подобрать значение![]() параметраС
так, чтобы
параметраС
так, чтобы
![]() было решением задачи Коши -.
было решением задачи Коши -.
Часто
общее решение задается неявно уравнением
![]() .
Это уравнение называетсяобщим
интегралом дифференциального
уравнения.
.
Это уравнение называетсяобщим
интегралом дифференциального
уравнения.
Примеры решения задач
Убедиться, что
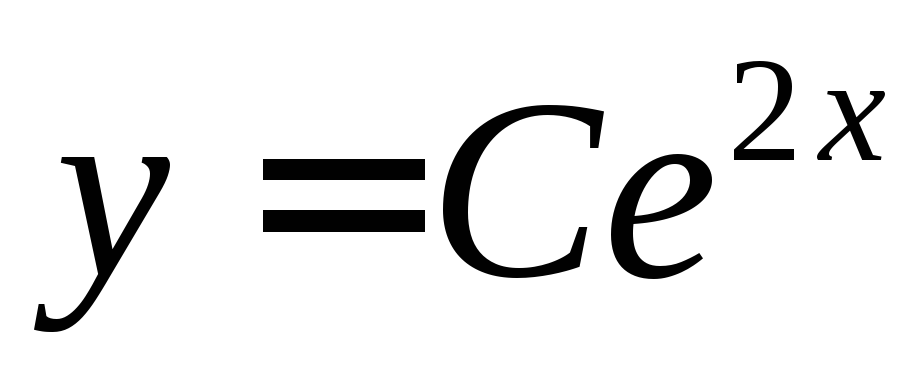 ,
, ,
, , является
общим решением уравнения
, является
общим решением уравнения
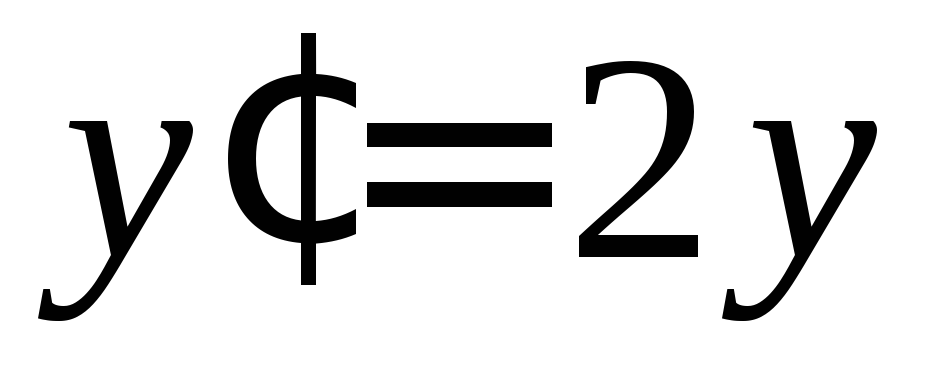 ,
, .
Сделать рисунок интегральных кривых.
Найти решение, удовлетворяющее
начальному условию
.
Сделать рисунок интегральных кривых.
Найти решение, удовлетворяющее
начальному условию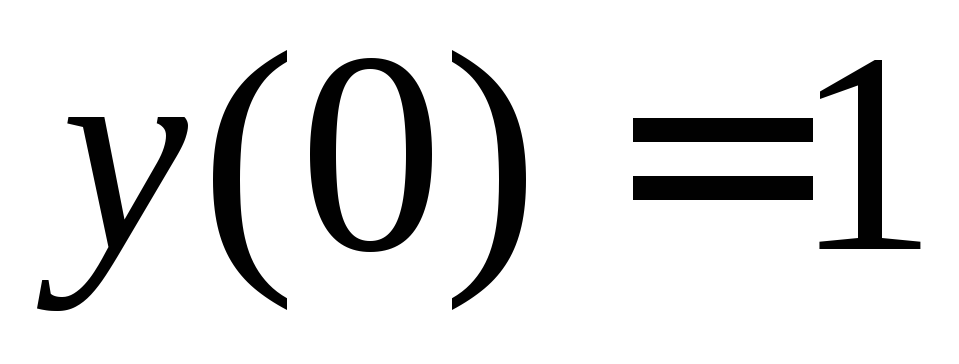 .
.
◄
С
= 1 y C=1 C=0,5 C=0 C=
– 0,5 C=
–1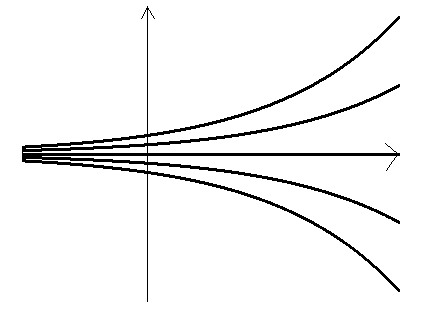
![]()
![]() как функция аргумента
как функция аргумента![]() является решением. Подставляя
является решением. Подставляя![]() и
и![]() в уравнение, получим тождество
в уравнение, получим тождество![]() :
:![]() .
2) Возьмем любую точку
.
2) Возьмем любую точку![]() и подберем параметрС так,
чтобы функция
и подберем параметрС так,
чтобы функция
![]() удовлетворяла начальному условию
удовлетворяла начальному условию![]() :
:
![]()
![]() ;
;
Т
Рис.
1
![]() –общее
решение.
–общее
решение.
Интегральные кривые изображены на рис. 1.
При
![]() получаем
получаем![]() ,
поэтому решение
,
поэтому решение![]() удовлетворяет начальному условию
удовлетворяет начальному условию![]() .
►
.
►
