№ 40

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями

Рассмотрим векторы и. Если угол между ними острый, то он будет, где φ – угол между прямой и плоскостью. Тогда.

Если угол между векторами итупой, то он равен. Следовательно. Поэтому в любом случае. Вспомнив формулу вычисления косинуса угла между векторами, получим.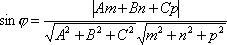

Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой и нормальный векторплоскости коллинеарны, т.е..

Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы иперпендикулярны.

Примеры.

1. Написать уравнение плоскости, проходящей через точку М₁(2;-3;4) параллельно прямым и.

Так как M₁ α, то уравнение плоскости будем искать в виде

.

Применяя условие параллельности прямой и плоскости, получим систему линейных уравнений 

Отсюда

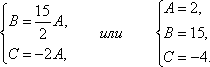
Итак, или.

2. Найти угол между прямой и плоскостью.

Направляющий вектор прямой . Нормальный вектор плоскости. Следовательно,

3. Найдите точку, симметричную данной М(0;-3;-2) относительно прямой .

Составим уравнение плоскости α перпендикулярной l. M α, . Следовательно,или.

Найдём точку пересечения прямой l и α:

Итак, N(0.5;-0.5;0.5). Пусть искомая точка М₁ имеет координаты М₁(x,y,z). Тогда очевидно равенство векторов , т.е. (0,5;2,5;2,5)=(х-0.5;у+0.5;z-0.5). Откуда x=1, y=2,z=3 или М₁(1;2;3)..

№41

ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ

Определение. Цилиндрической поверхностью называется поверхность, описываемая прямой (называемой образующей), остающейся параллельной некоторой данной прямой и пересекающей данную линию Z (называемую направляющей).

Рис.1

Пусть направляющая определяется уравнениями

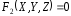и , (1)

а m, n, p – координаты направляющего вектора образующей цилиндрической поверхности. Канонические уравнения образующей имеют вид

, (2)

где x, y, z – текущие координаты, X,Y,Z – координаты точки, принадлежащей направляющей.

Исключая X, Y, Z из четырёх уравнений (1) и (2), получим искомое уравнение цилиндрической поверхности.

Рассмотрим частный случай. Пусть уравнение поверхности не содержит одной из переменных, для определённости z , то есть .

На плоскости Oxy это уравнение определяет некоторую кривую линию L.

В пространстве этому уравнению удовлетворяют все те точки пространства, первые две координаты которых совпадают с координатами линии L , то есть те точки пространства, которые проектируются на плоскость Oxy в точки линии L. Совокупность всех точек есть прямая параллельная оси Oz, проходящая через точку . Следовательно, совокупность всех точек, удовлетворяющих уравнению, есть поверхность, описываемая прямой, параллельной осиOz и пересекающих линию L, то есть цилиндрическая поверхность.

Рис.2

Аналогично, – уравнение цилиндрической поверхности, образующая которой параллельно осиOy; - уравнение цилиндрической поверхности с образующей, параллельной осиOx.

Перечислим прямые цилиндры с образующей, параллельной оси Oz:

1) – эллиптический цилиндр с направляющей – эллипсом в плоскостиOxy. Частным случаем эллиптического цилиндра является прямой круговой цилиндр, то есть .

Рис 3.

2) - гиперболический цилиндр с направляющей – гиперболой плоскостиOxy.

Рис.4

3) - параболический цилиндр с направляющей – параболой в плоскостиOxy.

Рис.5

КОНИЧЕСКИЕ ПОВЕРХНОСТИ

Определение. Конической поверхностью называется поверхность, описываемая прямой (образующей конуса), проходящей через данную точку (вершину конуса) и пересекающей данную линию (направляющую конуса).

Рис.6

Пусть направляющая задана уравнениями

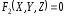и (1)

вершиной является точка M_o(x_o,y_o,z_o).

Канонические уравнения образующей конуса, проходящей через точку М_о и точку М(X,Y,Z), лежащую на направляющей, имеют вид:

. (2)

Исключая из (1) и (2) X,Y,Z, получим искомое уравнение конической поверхности.

Пример 1. Составить уравнение конуса с вершиной в начале координат и направляющей ,.

Образующая имеет канонические уравнения

, то есть .

Исключая X,Y,Z из уравнений

,

,

получим уравнение эллиптического конуса: . (3)

Рис.7

Пример 2. Составить уравнение конуса с центром в начале координат и направляющей ,.

Образующей искомого конуса является прямая:

.

Исключая X,Y,Z из уравнений направляющей и образующей, получим уравнениеили.

Обратим внимание, что полученное уравнение совпадает с уравнением (3).

Этот же конус можно получить, взяв в качестве направляющей параболу. Объясняется это сечениями конуса различными плоскостями. Подробнее об этом ниже.

ПОВЕРХНОСТИ ВРАЩЕНИЯ

Составить общее представление о большинстве поверхностей второго порядка можно, рассматривая поверхности вращения.

Определение. Поверхностью вращения вокруг оси d называется поверхность, каждое сечение которой, перпендикулярное оси d, является окружностью с центром, лежащим на этой оси.

Рассмотрим линию L, которая вместе с осью d лежит в плоскости Р. Будем вращать эту линию вокруг оси, при этом каждая точка линии опишет окружность, а вся линия L опишет поверхность вращения.

Введём систему координат. Выберем начало прямоугольной декартовой системы координат на оси d, ось Oz направим вдоль оси d, ось Ox поместим в плоскости P перпендикулярно оси Oz. Допустим, что линия L имеет в этой системе координат уравнение . Выведем уравнение поверхности вращения этой линии вокруг осиOz. Для этого выберем на поверхности произвольную точку M(x,y,z). Расстояние от неё до оси Oz равно . Через точкуМ проходит окружность, описываемая при вращении некоторой точки плоскости Р. Обозначим эту точку М_о, а её координаты в системе Oxz (x_o,y_o) (в системе Oxyz она будет иметь координаты (x_o,0,z_o)), очевидно что ,.

Точка М лежит на поверхности вращения тогда и только тогда, когда на ней лежит точка М_о, а, следовательно, и симметричная с ней относительно оси Oz точка . Чтобы точкиМ_о и лежали на поверхности, необходимо и достаточно, чтобы координаты хотя бы одной из них удовлетворяли уравнению линииL, то есть чтобы . Получим условие для координат точки

М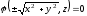. (1)

Это и есть уравнение поверхности вращения линии L вокруг оси Oz.

Случай, когда уравнение (1) не имеет вещественных решений, не исключается. В этом случае говорят о мнимой поверхности.

Эллипсоиды*

Эллипсоидом называется поверхность, задаваемая в некоторой декартовой системе координат уравнением  (3.26) Числа а, b, с называются полуосями эллипсоида. Выясним форму эллипсоида. Поскольку текущие переменные х, у, z входят в уравнение (3.26) в четных степенях, эллипсоид симметричен относительно каждой координатной плоскости. Рассмотрим сечение эллипсоида координатными плоскостями. Плоскость 0ху имеет уравнение , поэтому сечение эллипсоида плоскостью 0хузадается системой уравнений:   откуда имеем  (3.27) Система (3.27) показывает, что плоскость 0ху пересекает эллипсоид по эллипсу с полуосями а, b. Аналогично для плоскостей 0yz, 0xz соответственно получаем в сечении эллипсы: Можно показать, что любая плоскость, параллельная координатной плоскости, пересекает эллипсоид по некоторому эллипсу. Общий вид эллипсоида представлен на рис. 3.36.

Гиперболоиды*

Однополостным гиперболоидом называется поверхность, задаваемая в некоторой декартовой системе координат уравнением  (3.28) Эта поверхность имеет три плоскости симметрии (координатные плоскости). Выясним, какую форму имеет однополостный гиперболоид, для этого рассмотрим сечения его координатными плоскостями. В плоскости 0yz получаем: (3.29) – гиперболу с действительной полуосью b и мнимой полуосью с (в плоскости 0уz) (рис. 3.37). Аналогично,  (3.30) В сечении гиперболоида плоскостью 0xz также получаем гиперболу с действительной полуосью а и мнимой полуосью с. Пересекая гиперболу плоскостью 0ху в сечении получаем эллипс: с полуосями а и b. Всякая плоскость, параллельная плоскости 0ху (она имеет уравнение z = h, hR), пересекает однополостный гиперболоид по линии:  (3.31) Преобразуем систему (3.31):  (3.32) Система (3.32) задает эллипс (рис. 3.37), лежащий в плоскости z = h и имеющий своими полуосями: . Однополостный гиперболоид (3.28) не пересекает ось 0z, она служит осью симметрии для гиперболы (3.29) и гиперболы (3.30) и называется осью гиперболоида (3.28). Уравнение также задает однополостный гиперболоид, но его осью служит 0у, а для однополостного гиперболоида осью является ось 0х. Двуполостным гиперболоидом называется поверхность, определяемая в некоторой декартовой системе координат уравнением: Рассмотрим сечения этой поверхности координатными плоскостями:  (3.33)  (3.34) Система (3.33) задает в плоскости 0xz гиперболу с действительной полуосью с и мнимой полуосью а, система (3.34) – в плоскости 0уz также гиперболу с действительной полуосью с и мнимой – b. С плоскостью 0ху двуполостный гиперболоид пересечения не имеет. Действительно, системе: не удовлетворяет ни одна точка пространства. Рассмотрим сечение этого гиперболоида плоскостью, параллельной 0ху и удаленной от нее на расстояние :. Из этой системы получаем систему:, которая задает эллипс (рис. 3.38) в плоскостиz = h с полуосями . Ось 0z является общей осью симметрии для гипербол (3.33) и (3.34) и называется осью двуполостного гиперболоида. Уравнения:  (3.35)  (3.36) также задают двуполостные гиперболоиды, для (3.35) осью служит 0у, а для (3.36) – 0x.

Параболоиды*

Эллиптическим параболоидом называется поверхность, определяемая в некоторой декартовой системе координат уравнением:  , (3.37) где р и q одного знака. П усть ,, тогдаz 0, причемz = 0 при х = 0 и у = 0. Следовательно, с плоскостью 0ху эта поверхность имеет единственную общую точку 0(0, 0, 0). Рассмотрим сечение параболоида плоскостью z = h, (эта плоскость параллельна плоскости 0ху):   Видим, что сечение – эллипс с полуосями . Сечения с плоскостями 0ху и 0уz являются параболами:   причем 0z является их общей осью (рис. 3.39). Oсь 0z является осью параболоида (3.37). Если ,, то параболоид будет располагаться ниже плоскости 0ху. Гиперболическим параболоидом называется поверхность, уравнение которой имеет вид: , (3.38) где р и q одинакового знака. П усть ,. Рассмотрим сечения этой поверхности плоскостями 0xz и 0yz, получим, соответственно, параболы , причем ветви первой направлены вверх, а ветви второй – вниз (рис. 3.40). С плоскостью 0ху параболоид имеет сечение , что равносильно двум системам:  (3.39) Системы (3.39) задают в плоскости 0ху две прямые, проходящие через начало координат. Пусть плоскость параллельна 0ху и удалена от нее на h (), тогда в пересечении с параболоидом (3.38) получится гипербола  (3.40) При гипербола (3.40) имеет действительную полуось, мнимую полуось(рис. 3.40,L₃). При гипербола (3.40) имеет действительную полуось, а мнимую –(рис. 3.40,L₄). ^

№42

Определение предела по Коши и Гейне

Пусть функция f (x) определена на некотором открытом интервале X, содержащем точку x = a. (При этом не требуется, чтобы значение f (a) было обязательно определено.)  Число L называется пределом функции f (x) при , если для каждогосуществует такое число, что

при условии

Данное определение предела известно как - определение или определениеКоши.  Существует также определение предела функции по Гейне, согласно которому функция f (x) имеет предел L в точке x = a, если для каждой последовательности , сходящейся к точкеa, последовательность сходится кL. Определения предела функции по Коши и Гейне эквивалентны. 

ОДНОСТОРОННИЕ ПРЕДЕЛЫ

До сих пор мы рассматривали определение предела функции, когда x→a произвольным образом, т.е. предел функции не зависел от того, как располагалось x по отношению к a, слева или справа от a. Однако, довольно часто можно встретить функции, которые не имеют предела при этом условии, но они имеют предел, если x→a, оставаясь с одной стороны от а, слева или справа (см. рис.). Поэтому вводят понятия односторонних пределов.

Если f(x) стремится к пределу b при x стремящемся к некоторому числу a так, что xпринимает только значения, меньшие a, то пишут и называютbпределом функции f(x) в точке a слева.

Таким образом, число b называется пределом функции y=f(x) при x→aслева, если каково бы ни было положительное число ε, найдется такое число δ (меньшееa), что для всех выполняется неравенство.

Аналогично, если x→a и принимает значения большие a, то пишут и называютb пределом функции в точке а справа. Т.е. число b называется пределом функции y=f(x) при x→a справа, если каково бы ни было положительное число ε, найдется такое число δ (большее а), что для всех выполняется неравенство.

Заметим, что если пределы слева и справа в точке a для функции f(x) не совпадают, то функция не имеет предела (двустороннего) в точке а.

Примеры.

1. Рассмотрим функцию y=f(x), определенную на отрезке [0,1] следующим образом

Найдем пределы функции f(x) при x→3. Очевидно, , а.

2. 

3. .

4. .

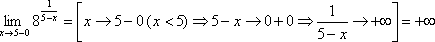Основные теоремы о пределах

 

Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.

  .

Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).

  .

Теорема 3. Предел постоянной равен самой постоянной.

.

Доказательство. f(x)=с,    докажем, что    .

Возьмем  произвольное >0. В качестве  можно взять любое

положительное число. Тогда при 

.

Теорема 4. Функция не может иметь двух различных пределов в

одной точке.

Доказательство. Предположим противное. Пусть

  и  .

По теореме о связи предела и бесконечно малой функции:

f(x)-A= - б.м. при ,

f(x)-B= - б.м. при .

Вычитая эти равенства, получим:

 B-A=-.

Переходя к пределам в обеих частях равенства при , имеем:

B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.

Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при , то и алгебраическая сумма имеет предел при , причем предел алгебраической суммы равен алгебраической сумме пределов.

.

Доказательство. Пусть ,  ,   .

Тогда, по теореме о связи предела и б.м. функции:

 где  - б.м. при.

Сложим алгебраически эти  равенства:

f(x)+g(x)-h(x)-(А+В-С)=,

где б.м. при  .

По теореме о связи предела и б.м. функции:

А+В-С=.

Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при , то и произведение имеет предел при, причем предел произведения равен произведению пределов.

.

Следствие. Постоянный множитель можно выносить за знак предела.

.

Теорема 7. Если функции f(x) и g(x) имеют предел при ,

причем , то и их частное имеет предел при , причем предел частного равен частному пределов.

,  .

№43

Первый замечательный предел

Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.

Задание. Найти предел 

Решение. Воспользуемся заменой и первым замечательным пределом.

Ответ. 

Пример

Задание. Найти предел 

Решение. Разложим тангенс на синус и косинус и воспользуемся свойствами пределов.

Ответ. 

Следствия из первого замечательного предела

1°   

2°   

3°   

4°   

Второй замечательный предел

здесь е - число Эйлера.

Пример

Задание. Найти предел 

Решение. Подставим , получим неопределенность и для решения предела воспользуемся вторым замечательным пределом.

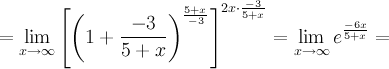
Ответ. 

Следствия из второго замечательного предела

1°   

2°   

3°   

4°   

5°   

6°   

№44

Бесконечно малые и бесконечно большие функции. Их свойства

 

Определение 1. Функция  называется бесконечно малой (б.м.) функцией при , если ее предел при равен нулю.

 <=>  , для всех х, удовлетворяющих неравенству , будет выполняться неравенство .

Определение 2. Функция  называется бесконечно большой (б.б.) функцией при , если ее предел при равен + (-).

Пример. Функция   при    - б.м., при    - б.б., при  не является ни б.б. ни б.м.

Теорема 1 (о связи предела и бесконечно малой функции). Если функция  имеет предел , то разность между функцией и значением предела есть функция, бесконечно малая при .

Доказательство. Необходимо показать, что

 <=> f(x)-A  б.м. функция при .

Так как , то

 , для  будет выполняться неравенство .

Сравним это с определением б. м. функции:

 , для  будет выполняться неравенство .

Сравнивая определения предела функции и б. м. функции, видим, что f(x)-A  -  б.м. при .

Теорема 2. Алгебраическая сумма конечного числа бесконечно малых при  функций есть функция бесконечно малая при .

Доказательство. Пусть  - б.м. функции при .

Надо доказать, что  есть б.м. функция при.

Возьмем >0, тогда и .

Так как  - б.м. при , , ,    ;

(2.1)

так как  - б.м. при , , ,    ;            

так как  - б.м. при , , ,    .

Возьмем , тогда при  будут выполняться все три неравенства (2.1) одновременно.

.

Итак, для >0 мы нашли  такое, что при всех  выполняется неравенство , =>  есть б.м. функция при.

Теорема 3. Произведение бесконечно малой при  функции на ограниченную в некоторой окрестности точки а функцию есть бесконечно малая функция при .

Доказательство.  - б. м. при функция;

f(x) - ограниченная в некоторой окрестности точки а функция.

Докажем, что   · f(x) – б. м. функция при .

Поскольку f(x) - ограниченная в некоторой окрестности точки а функция, то  и К такие, что при х

(2.2)

    | f(x)| < К.

Возьмем произвольное >0 и рассмотрим число ,

так как  - б. м. при функция, , что х:

(2.3)

    ||<.

Возьмем , тогда при  будут выполняться оба неравенства (2.2) и (2.3) одновременно.

<

Итак, для >0  мы нашли  такое, что при всех х, удовлетворяющих , выполняется неравенство |· f(x)|< , =>    · f(x) – б. м. функция  при .

Теорема 4. Произведение конечного числа бесконечно малых при  функций есть функция, бесконечно малая при .

Теорема 5 (о связи бесконечно малой и бесконечно большой функций). Если  - б. м. при функция и 0 в некоторой окрестности точки а, то функция  есть б. б. функция при .

Если  - при  б. б. функция, то функция  есть б. м. функция при .