- •Предмет, объект и методы статистической науки.
- •Основные этапы статистического исследования. Научные принципы организации статистической информации.
- •Абсолютные статистические величины, методы их изменения.
- •Относительные величины, их виды и порядок определения.
- •Средние величины в статистике и способы их вычисления.
- •Средняя арифметическая и средняя гармоническая.
- •Система показателей вариации и способы их вычисления.
- •Правило сложения дисперсий. Виды дисперсий: общая, межгрупповая и внутригрупповая.
- •Коэффициент детерминации и коэффициент корреляционного отношения: их использование в изучении связей.
- •Теоретические основы выборочного наблюдения.
- •Классификация ошибок выборки. Расчет ошибок выборки (репрезентативности) при различных способах отбора.
- •Определение объема (численности) выборочной совокупности.
- •Понятие рядов динамики, их виды.
- •Цепные и базисные показатели ряда динамики и способы их вычисления.
- •Средние характеристики динамики
- •Хронологические средние и способы их вычисления.
- •Статистическое изучение сезонных колебаний.
- •Методы выявления основной тенденции в развитии социально- экономических явлений.
- •Понятие статистических индексов, их виды.
- •Агрегатные индексы, их виды и принципы построения. Взаимосвязь агрегатных индексов.
- •Среднеарифметический индекс и условия его применения.
- •Среднегармонический индекс и условия его применения.
- •Показатели численности населения.
- •Показатели естественного и механического движения населения.
- •Расчёт перспективной численности населения.
- •Статистика трудовых ресурсов. Показатели естественного и механического движения трудовых ресурсов.
- •Показатели уровня занятости и безработицы, демографической и пенсионной нагрузки, коэффициент замещения.
- •Состав экономически активного населения.
- •Показатели численности персонала предприятия.
- •Показатели движения персонала предприятия.
- •Фонды рабочего времени и показатели их использования.
Цепные и базисные показатели ряда динамики и способы их вычисления.
Для анализа ряда динамики используют: абсолютный прирост, темп прироста, темп роста, абсолютное значение на 1% прироста.
|
Цепной (где - уровень сравниваемого ряда; - уровень предшествующего периода; - уровень базисного периода) |
Базисный |
|
Абсолютный прирост - определяется как разность между двумя уровнями динамического ряда и показывает, на сколько единиц данный уровень ряда превышает уровень другого периода. Один и тот же по величине абсолютный прирост может означать разную интенсивность изменения. | |
|
|
|
|
Темп роста - определяется как отношение двух сравниваемых уровней и показывает, во сколько раз данный уровень превышает уровень превышает уровень базисного периода | |
|
|
|
|
Темп прироста - ) показывает, на сколько процентов уровень данного периода больше или меньше определенного уровня, характеризует относительную скорость изменения уровня ряда в единицу времени | |
|
|
|
|
Абсолютное значение на 1% прироста - Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1% прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за тот же промежуток времени | |
|
| |
Между цепными и базисными показателями ряда динамики существуют следующие соотношения:
Сумма цепных приростов=базисному,
Произведение цепных коэф-в роста=базисному:
 ;
;
Средние характеристики динамики
Средний уровень ряда. Методика вычисления показателей ряда динамики аналогично для интервальных и моментных рядов, разница существует лишь в определении среднего уровня ряда.
Для
интервального ряда средний уровень
ряда рассчитывается по средней
арифметической:
 .
.
Для
моментного ряда расчет производится
по средней хронологической:

Средний абсолютный прирост:
 или
или  , гдеm
– кол-во цепных приростов, всегда на
один меньше.
, гдеm
– кол-во цепных приростов, всегда на
один меньше.
Средний темп роста:
 ;
;
 ;
;
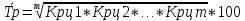 или
или 
Среднегодовой темп прироста:

Хронологические средние и способы их вычисления.
Средней хронологической называется величина, исчисленная из абсолютных величин, образующих ряды динамики.
Средний уровень моментного ряда динамики с равноотстоящими уровнями характеризует средняя хронологическая простая, которая исчисляется по формуле:
![]()
Средний уровень моментного ряда динамики с неравноотстоящими уровнями характеризует средняя хронологическая взвешенная, которая исчисляется по формуле:
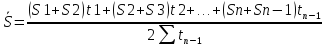
Средними хронологическими величинами пользуются для характеристики средних уровней явлений за определенные промежутки времени.
Статистическое изучение сезонных колебаний.
Сезонность — регул повторяющееся изменение явлений в динамике, связанное со сменой времен года, явлений природы, выполнением определенных работ и тд.. Сез. отражается на производственной деятельности с.х предприятий, влияет на работу пром предприятий ит.д. Сез характеризуется изменением сезонной составляющей РД, описывающей внутригодичные регулярные измен явлений. Внутригодичная динамики, имеющая периодический характер - сезонные колебания. Сез отрицательно влияет на результаты произв деятельности, вызывая нарушения ритмичности производства, поэтому хоз субъекты принимают меры для смягчения явл сезонности за счет рационального сочетания отраслей, механизации трудоемких процессов, создания агропром объединений. Для изучения временных периодических колеб уровня изучаемого явления во времени используют гармонический анализ. Целью гармон анализа является выявление и измерение сез колебаний в РД. В этом случае функцию, заданную в каждой точке изучаемого интервала времени, можно представить бесконечным рядом синусоидальных кривых. Для изучения и анализа сезонных колебаний строят модель сезонной волны. Моделью периодически изменяющихся уровней служит ряд Фурье
Измен значения гармоники дает возм максимально приблизить теоретические данные к эмпирическим. На практике k применяется равным от 1 до 4, t имеет радианную меру и является аргументом тригонометр функции.
Построение модели сез колебаний дает возможн определить длительность подъема и спада колебаний и вовремя принять соответств управленческое решение. Применение ряда Фурье оправдано лишь, если максимальные и минимальные сез колебания повторяются через равные промежутки времени.
Индексы сезонности
Индексы
сез- это показатели интенсивности
сезонных колебаний. В общем виде они
выражаются как отношение каждого уровня
РД к среднему и позволяют измерить
размах колебаний помес данных, однако
помес данные одного года являются
недостаточно надежными для выявления
законом периодич колебаний. Чаще для
этих целей исп месячные данные за ряд
лет, в частности за три года. В этом
случае рассчит среднюю из уровней
показателей, относящихся к одноименным
месяцам, затем из средних уровней рассчит
общую среднюю и отношение средн уровня
за каждый месяц к общ среднему уровню:
![]()