41 Определение гидравлического удара. Прямой и непрямой гидравлический удар. Скорость распространения ударной волны.

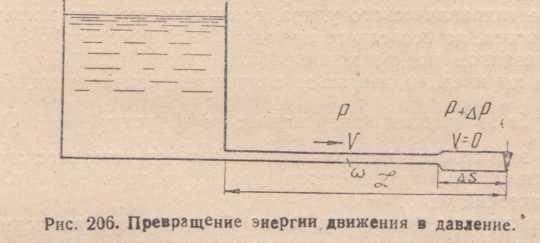
При быстром закрытии задвижки на трубе, по которой вода движется со скоростью V, происходит гидравлический удар. Энергия движущейся массы воды при остановке превращается в энергию давления, которое увеличивается на . Переход энергии движения в давление происходит сначала на длине (рис. 206), на которой вода останавливается и сжимается, а труба расширяется от повышения давления, а затем это состояние распространяется на всю трубу. Потерянное количество движения переходит в импульс силы , где р— плотность воды, а - площадь поперечного сечения трубы. . Заменяя , получим . Здесь - напор; - скорость распространения повышения давления вдоль водовода, которую обозначают через а. Окончательно. Это формула Жуковского, выведенная им еще в 1898 г. Им же было дано выражение для определения скорости ударной волны а.

Скорость ударной волны а зависит от диаметра трубы d, толщины ее стенки о, от материала трубы и свойств жидкости. Величина . Здесь е — объёмный модуль упругости воды;Е— модуль упругости стенок трубы. Для стальных чугунных труб скорость ударной волны составляет около 1000 м/сек, для асбоцементных около 700 м/сек, а для резиновой трубки — несколько десятков метров в секунду. Из формулы Жуковского следует, что для металлических труб при скорости движения ударной волны около 1000 м/сек каждый метр потерянной скорости дает повышение напора над тем напором, который имел место в трубе до закрытия задвижки, примерно на 100 м. Такое повышение напора имеет место в том случае, если полное закрытие задвижки произойдёт за время t, меньшее, чем время пробега ударной волной двойного расстояния от резервуара до задвижки, равное . Если же задвижку закрыть за время большее , то сила удара уменьшается и тем больше, чем медленнее закрывать задвижку.

Прямой удар происходит при времени закрытия задвижки

t3 < 2L/C

где L - расстояние до резервуара способного поддерживать постоянное давление.

C - скорость распространения ударной волны.

Непрямой гидравлический удар при t3 > 2L/C. Такой удар характеризуется меньшей силой, чем прямой удар

Внезапное повышения давления ”р или напора ”H может быть рассчитано по методу Жуковского.

Скорость распространения ударной волны

Еж – модуль объемной упругости жидкости, для воды Е=2.03*10і МПа

Б - плотность жидкости Б= 1000 кг/мі (вода)

Еж/Б – скорость распространения звука в жидкости

(Еж/Б=1425 м/с- для воды )

Етр – модуль упругости материала стенок трубы. D – диаметр, ґ – толщина

Для воды отношение Е/Етр:

стальные трубы – 0,01; чугунные – 0,02

Коеф-т K, для тонкостенных трубопроводов (стальных, чугунных, полиэтиленовых) =1

Для железобетонных К=1/(1+9.5 ±’). Обычно ±=0,015….0.05

Время, за которое ударная волна пройдёт путь до резервуара и вернётся обратно к задвижке, Т=2L/C называется фазой удара. Процесс при гидравлическом ударе на рис.

Скорость распространения гидравлической ударной волны в трубопроводе

Изменения давления и скорости потока в трубопроводах происходят не мгновенно в связи с упругостью твёрдых стенок трубы и сжимаемостью р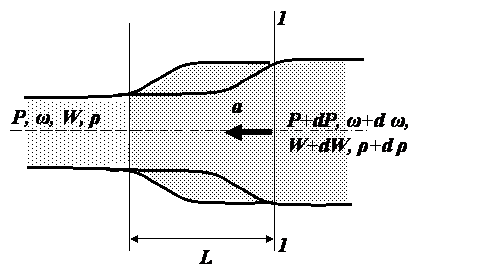абочей среды, а с некоторой конечной скоростью, обусловленной необходимостью компенсации упругих деформаций жидкости и трубы. Рассмотрим случай когда в трубопроводе длинойL и площадью сечения Й под давлением Р находится жидкость, плотность которой Б.Предположим, что в момент времени t в сечении 1 – 1 давление повысится на величину dp. Это повышение вызывает увеличение плотности на величину dБ,а также расширение внутреннего диаметра трубы. Следовательно, площадь проходного сечения увеличится на величину dЙ. В результате увеличится объём W участка трубы на величину dW. За счёт этого произойдет увеличение массы жидкости находящейся в трубе на участке длиной L. Масса увеличится за счёт увеличения, во-первых, плотности жидкости, во-вторых, за счёт увеличения объёма W.

Такая ситуация рассматривалась при выводе уравнения неразрывности потока в дифференциальной форме, с той только разницей, что там рассматривалось лишь изменение массы во времени, без учёта вызвавших это изменение причин . По аналогии с приведённым уравнением запишем выражение, описывающее изменение массы за счёт изменения давления

.

Жидкость под действием указанного повышения давления устремится с некоторой скоростью а в слои с меньшим давлением, в которых также будет повышаться плотность и увеличиваться напряжение в стенках трубопровода, способствующее увеличению площади трубопровода. В связи с этим потребуется некоторое время на распространение этих деформаций вдоль трубопровода.