5. Выбор и расчет посадки с натягом

d₁₅=25мм, Н*м [1]П.1.1

Посадки с натягом предназначены для неподвижных неразъемных соединений деталей без дополнительного крепления винтами, гайками, шпонками, штифтами и т.д. Относительная неподвижность деталей при этом достигается за счет напряжений, возникающих в материале сопрягаемых деталей вследствие действия деформаций их контактных поверхностей. Шероховатость принимаем равной R_zd=8 мкм, R_zD=10 мкм. Корпус и ось изготовлены из Сталь 45(µ=0.3) [1] с.11.

Рис 5.1. Схема сопряжения с натягом.

Определяем не заданные геометрические параметры деталей сопряжения, необходимые для последующего расчета по формулам [1], c 11:

l =(1,4-1,6) d_н.с (5.1)

d_н.с.– номинальный диаметр зубчатого колеса, мм,

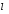– ширина корпуса;

l =1,5*25=37,5 мм;

Находим величину минимального удельного давления, возникающего на контактируемых поверхностях и необходимого для передачи крутящего момента. [1], c.12:

(5.2) где f – коэффициент трения, выбираемый из [2] с.334.

Принимаем f=0.095, поскольку обе сопрягаемые детали изготовлены из стали [2] с.334.

Па

Рассчитываем величину минимально необходимого натяга, обеспечивающего неподвижность соединения, используя известное соотношение для определения напряжений и упругих перемещений в толстостенных цилиндрах [1], с.12:

, (5.3)

где и – модули упругости материалов втулки (ступицы) и вала,

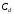и – коэффициенты Лямэ, определяемые по формулам[1], с. 12:

_{Для массивного корпуса [2], с.362:}

_{Для сплошного вала [2], с.362:}

где и – коэффициенты Пуассона для ступицы и вала.

Значения и выбираем по таблице [1], таблица 1.06.

Принимаем и из [1], таблица 1.106.

Подсчитаем величину минимального натяга по ф-ле (5.3):

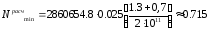мкм.

Определяем наименьший допустимый натяг с учетом уменьшения действительного натяга за счет смятия неровностей при запрессовке [1], с.13:

(5.4)

Рассчитываем максимально допустимое удельное давление ,при котором отсутствует пластическая деформация на контактных поверхностях деталей по [1],с.13.

Па (5.5)

МПА_(5.6)

_где  σ_Td и σ_TD пределы текучести вала и втулки соответственно, Мпа, σ_Td=850 МПа, σ_TD=340 Мпа.[2],с.362.

Находим величину наибольшего расчетного натяга, для этого возьмем минимальное значение допустимого удельного давления [1],с.13:

(5.7)

Вычисляем наибольший допустимый натяг с учетом среза и смятия неровностей [1],с.13:

(5.8)

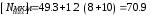
По [2], табл. 1.30 выбираем посадку.

Выбираем посадку. мм.

Определим наибольший и наименьший натяги:

Верхнее предельное отклонение ES=+0.013мм.

Нижнее предельное отклонение EI=0

Верхнее предельное отклонение es=+0.054мм.

Нижнее предельное отклонение ei=+0.041мм.

Наибольший натяг N_max=es-EI=0.054-0=0.054 мм.

Наименьший натяг N_min=ei-ES=0.041-0.013=0.028 мм.

Определяем запас прочности при сборке:

(5.11)

Запас прочности при эксплуатации:

(5.9)

В результате получили, что >: условие выполняется.

Находим необходимое усилие для запрессовки деталей без применения термических методов сборки [1],с.14:

, (5.10)

где – коэффициент трения при запрессовке [1],с14.

– удельное давление при максимальном натяге выбранной посадки, определяемое [1],с.14:

(5.11)

Зная величину удельного давления при максимальном натяге выбранной посадки, вычисляем необходимое усилие для запрессовки деталей без применения термических методов сборки:

Рисунок 5.2. Схема полей допусков

Рисунок 5.3. Ось Рисунок 5.4. Корпус