10.3. Кратные интегралы

Пусть функция f(x,y) определена в ограниченной замкнутой областиDплоскости. Разобьем областьDнаэлементарных областей, имеющих площади₁,₂, …,_пи диаметрыd₁,d₂, …,d_п.

Выберем в каждой элементарной области произвольную точку Р_к(_к,_к) и умножим значение функции в этой точкеР_кна площадь области.

называется интегральной суммой.

Двойным интегралом от функцииf(x,y) по областиDназывается предел интегральной суммы при условии, что наибольший из диаметров областей0.

Двойной интеграл обладает свойствами:

1. .

2. .

3. Если , то

.

В декартовых координатах двойной интеграл записывается в виде .

Рассмотрим вычисление двойных интегралов. Пусть область D расположена в пределах по оси ОХ

Двойной интеграл можно записать через повторные интегралы:

,

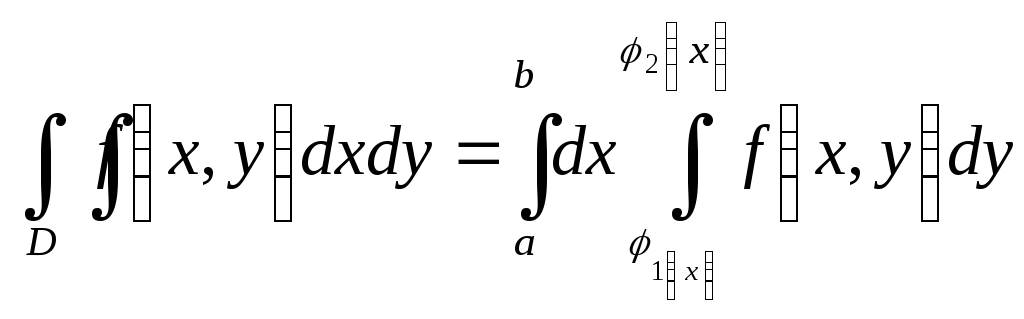причем сначала вычисляется

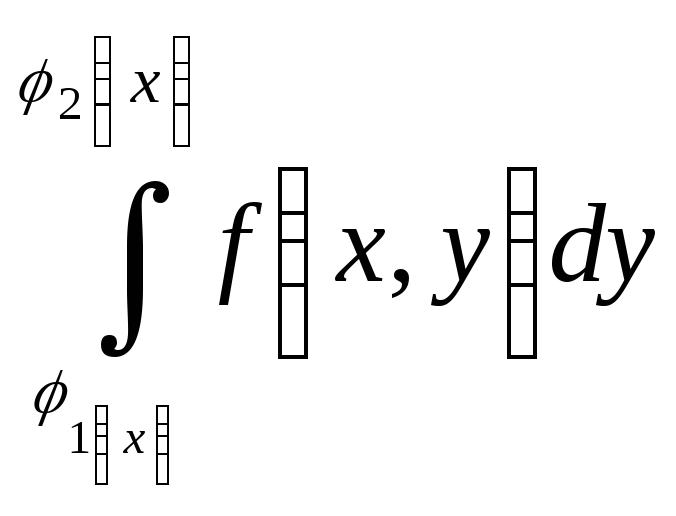
где переменная считается постоянной.

Пусть область Dрасположена в пределах по оси ОУ .

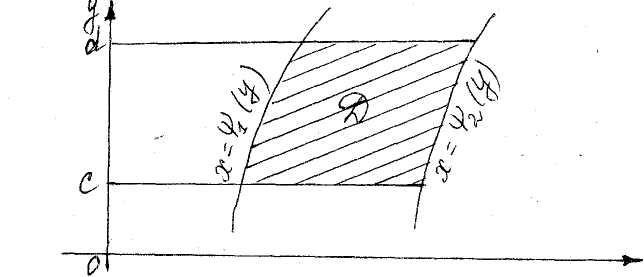
Двойной интеграл запишется через повторные интегралы:

,

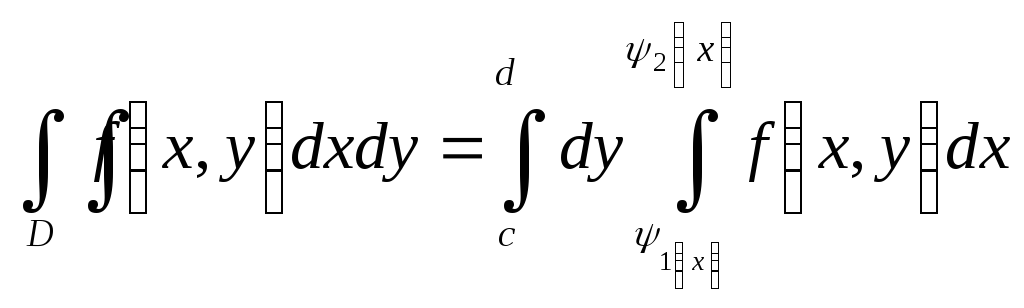где сначала вычисляется

,

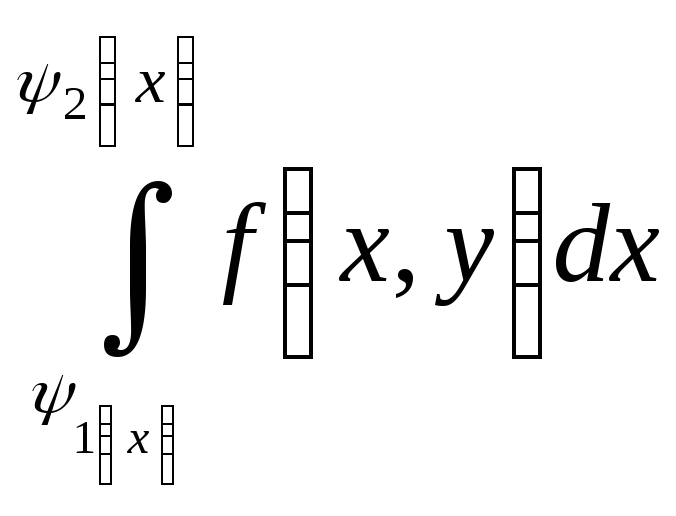здесь переменная считается постоянной.

Пусть функция f(x,y,z) определена в ограниченной замкнутой пространственной областиТ. Разобьем областьТнапэлементарных областейТ₁,Т₂,…,Т_пс диаметрамиd₁,d₂,…,d_пи объемамиV₁,V₂, …,V_п. В каждой элементарной области возьмем произвольную точкуР_к(_к,_к,_к) и умножим значение функции в точкеР_к на объем этой области.

Интегральной суммой для функции f(x,y,z) по областиТназывается сумма вида.

Тройным интегралом от функции f(x,y,z) по областиТназывается предел интегральной суммы при условии, что наибольший из диаметров элементарных областей стремится к нулю:.

Свойства тройных интегралов аналогичны свойствам двойных интегралов.

В декартовых координатах тройной интеграл записывается в виде: .

Пусть область интегрирования Топределяется неравенствами:х₁ х х₂;у₁(х)у у₂(х),z₁(х,у)z z₂(х,у), гдеу₁(х),у₂(х),z₁(х,у) иz₂(х,у) – непрерывные функции. Тогда тройной интеграл от функцииf(x,y,z) вычисляется по формуле:.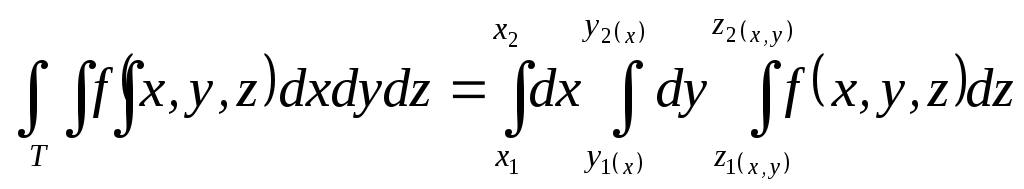

Контрольные вопросы

1. Как определяется максимум и минимум функции двух аргументов?

2. Назовите необходимые и достаточные условия экстремума функции двух аргументов.

3. По какому алгоритму находится экстремум функции двух аргументов?

4. Приведите пример нахождения экстремума функции двух аргументов в экономике.

5. Что такое двойной интеграл?

6. Что такое тройной интеграл?

Тема 11. Дифференциальные уравнения первого порядка

11.1. Основные сведения о дифференциальных уравнениях

Дифференциальным уравнением называется всякое соотношение между независимыми переменными, функцией от них и производными этой функции по этим переменным. Исследование закономерностей различных экономических процессов часто приводит к построению моделей, основой которых являются дифференциальные уравнения.

Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным, если от нескольких – то уравнением в частных производных. В дальнейшем будем рассматривать только обыкновенные дифференциальные уравнения.

В общем случае такие уравнения можно записать в виде:

,

где есть функция аргумента, а– производные этой функции.

К дифференциальным уравнениям, относятся уравнения, связывающие дифференциалы независимой переменной и функции от неё. Например: .

Порядком дифференциального уравнения называется максимальный порядок производной, входящей в уравнение. Так, например, уравнения ипервого порядка; уравненияивторого порядка.