
- •Тема 9. Дифференциальное исчисление функций нескольких переменных
- •9.1. Основные сведения о функциях
- •Нескольких переменных
- •9.2. Частные производные и дифференциалы функции двух аргументов
- •9.3. Производная по направлению, градиент
- •Контрольные вопросы
- •Тема 10. Экстремум функции двух аргументов. Интегральное исчисление функций нескольких переменных
- •10.1. Максимум и минимум функции двух аргументов
- •10.2. Алгоритм нахождения экстремума функции двух аргументов
- •10.3. Кратные интегралы
- •Контрольные вопросы
- •Тема 11. Дифференциальные уравнения первого порядка
- •11.1. Основные сведения о дифференциальных уравнениях
84 85
Тема 9. Дифференциальное исчисление функций нескольких переменных
9.1. Основные сведения о функциях
Нескольких переменных
Многим явлениям, в том числе и экономическим, присуща многофакторная зависимость. Например, спрос на товар зависит от его цены, качества изготовления и других показателей. Исследование таких зависимостей потребовало введения понятия функции нескольких переменных.
Пусть имеется
![]() переменных величин, и каждому набору
их значений
переменных величин, и каждому набору
их значений![]() соответствует по какому-то закону
соответствует по какому-то закону![]() одно значение переменной величины
одно значение переменной величины![]() .
В этом случае задана функция нескольких
переменных
.
В этом случае задана функция нескольких
переменных![]()
Переменные
![]() называются независимыми переменными
или аргументами. Все их допустимые
значения образуют область определения
функции. Все значения зависимой переменной
называются независимыми переменными
или аргументами. Все их допустимые
значения образуют область определения
функции. Все значения зависимой переменной![]() образуют множество значений функции
нескольких переменных.
образуют множество значений функции
нескольких переменных.
Функции нескольких переменных можно
задавать аналитически, то есть формулой,
при помощи таблиц, при помощи графика
для функций двух переменных:
![]() – это множество точек пространства с
координатами
– это множество точек пространства с
координатами![]() в системе координат
в системе координат![]() .
.
Например, предприятие производит
![]() видов продукции, которые реализуются
по ценам
видов продукции, которые реализуются
по ценам![]() ,
при объемах реализации
,
при объемах реализации![]() выручка будет задаваться линейной
функцией аргументов
выручка будет задаваться линейной
функцией аргументов![]() ,
то есть
,
то есть![]() .
Прейскурант автомастерской есть
табличный способ задания стоимости
ремонта в зависимости от выполненных
работ. Перечень этих работ – это область
определения функции, а стоимость всех
работ – значение функции. График функции
.
Прейскурант автомастерской есть
табличный способ задания стоимости
ремонта в зависимости от выполненных
работ. Перечень этих работ – это область
определения функции, а стоимость всех
работ – значение функции. График функции![]() изображен на рисунке.
изображен на рисунке.
Линией уровня функции двух переменных
![]() называется плоская кривая, получаемая
при пересечении графика этой функции
плоскостью
называется плоская кривая, получаемая
при пересечении графика этой функции
плоскостью![]() ,
где
,
где![]() – постоянная величина.
– постоянная величина.
Обычно линии уровня проецируются на
координатную плоскость
![]() ,
в этом случае их удобно анализировать.
,
в этом случае их удобно анализировать.
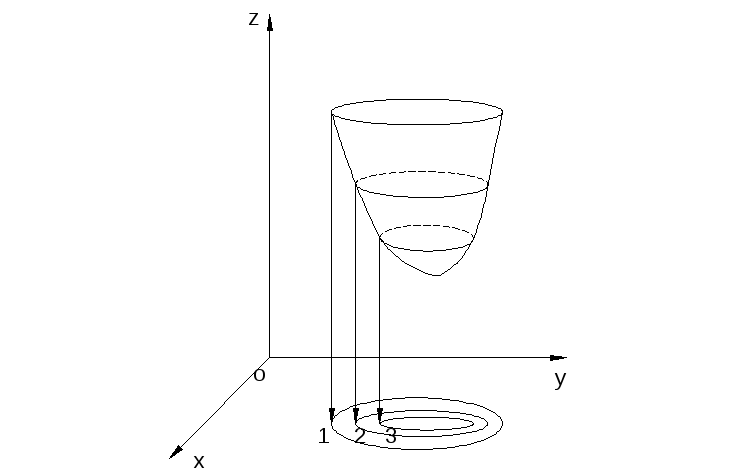
Линии уровня производственной функции
Кобба-Дугласа
![]() ,
где
,
где![]() – объем выпущенной продукции,
– объем выпущенной продукции,![]() – затраты капитала,
– затраты капитала,![]() – трудовые затраты, коэффициенты
– трудовые затраты, коэффициенты![]() ,
называются изоквантами и определяют
одинаковый выпуск продукции при различных
сочетаниях факторов
,
называются изоквантами и определяют
одинаковый выпуск продукции при различных
сочетаниях факторов![]() и
и![]() .
.
9.2. Частные производные и дифференциалы функции двух аргументов
Пусть функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() .
Придадим переменной
.
Придадим переменной![]() в точке
в точке![]() произвольное приращение
произвольное приращение![]() ,
оставляя значение переменной
,
оставляя значение переменной![]() неизменным.
Тогда соответствующее приращение
функции
неизменным.
Тогда соответствующее приращение
функции
![]()
называется частным приращением функции
по переменной
![]() в точке
в точке![]() .
.
Если существует предел
![]() ,
то он называется частной производной
функции
,
то он называется частной производной
функции![]() по переменной
по переменной![]() и обозначается одним из следующих
символов:
и обозначается одним из следующих
символов:
![]() .
.
Из определения следует, что частная
производная функции двух переменных
по переменной
![]() представляет собой обыкновенную
производную функции одной переменной
представляет собой обыкновенную
производную функции одной переменной![]() при фиксированном значении переменной
при фиксированном значении переменной![]() .
Поэтому частная производная вычисляется
по формулам и правилам вычисления
производных функций одной переменной.
.
Поэтому частная производная вычисляется
по формулам и правилам вычисления
производных функций одной переменной.
Аналогично определяется частная
производная функции
![]() по переменной
по переменной![]() и обозначается одним из символов:
и обозначается одним из символов:
![]() .
.
Например, найти частные производные
функции
![]() .
Частную производную
.
Частную производную![]() находим как производную функции
находим как производную функции![]() по аргументу
по аргументу![]() приy =const.
приy =const.
![]() .
.
Аналогично
![]() .
.
Частными производными второго порядка
от функции
![]() называются частные производные от ее
частных производных первого порядка и
обозначаются следующим образом:
называются частные производные от ее
частных производных первого порядка и
обозначаются следующим образом:
![]() .
.
Полный дифференциал функции или
дифференциал первого порядка от функции
![]() находится по формуле:
находится по формуле:
![]() .
.
Дифференциалом второго порядка от
функции
![]() называется дифференциал от ее полного
дифференциала. Если
называется дифференциал от ее полного
дифференциала. Если![]() и
и![]() – независимые переменные и функция
– независимые переменные и функция![]() имеет непрерывные частные производные,
то дифференциал второго порядка
вычисляется по формуле:
имеет непрерывные частные производные,
то дифференциал второго порядка
вычисляется по формуле:
![]() .
.
