уч. пос. 2012 стр. 72-83

82 83

.

По этой формуле вычисляют значения определенного интеграла в два этапа: на первом этапе находят первообразную функцию для функции ; на втором применяется фактически эта формула – находится приращение первообразной .

Пример. Вычислить определенные интегралы:

а) ; б) ; в) .

Решение. а) .

б) .

в) 64+128+20-4+16+10=234.

Замена переменной в определенном интеграле выполняется по формуле:

,

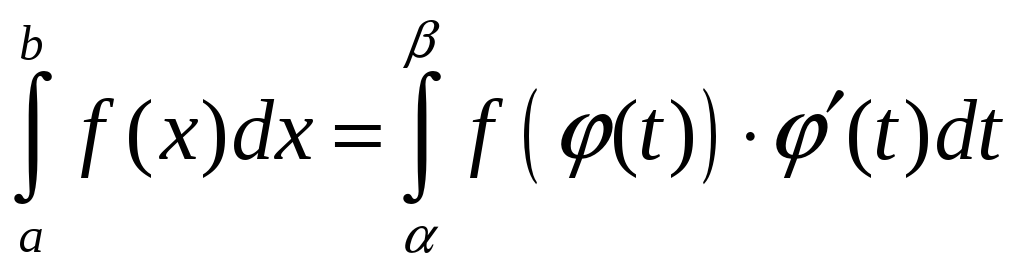где , , ; – новая переменная; и – новые пределы интегрирования.

Пример. Вычислить .

Решение.

.

Интегрирование по частям в определенном интеграле осуществляется по формуле:

.

Пример. Вычислить .

Решение.

8.3. Геометрические приложения определенного интеграла

Определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции, то есть фигуры, ограниченной графиком функции , двумя прямыми , и осью .

В этом состоит геометрический смысл определенного интеграла .

Если , то площадь фигуры, ограниченной графиком этой функции, двумя прямыми , и осью , находится по формуле .

Площадь криволинейной фигуры, ограниченной сверху и снизу соответственно линиями , , слева и справа – прямыми и , определяется формулой:

.

Например, вычислить площадь фигуры, ограниченной линиями и . Для построения фигуры найдем точки пересечения этих линий, решим систему:

, .

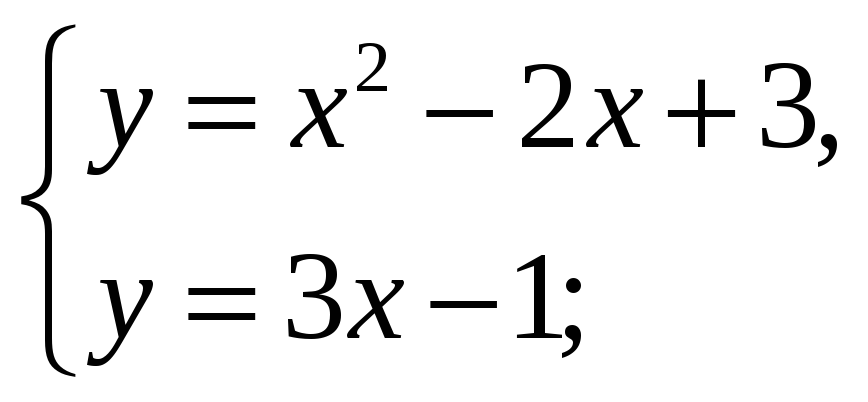
Откуда , и , . Выполним чертеж фигуры.

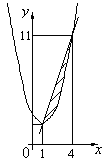
Находим искомую площадь :

(кв. ед. изм.).

Если плоская фигура имеет сложную форму, то ее следует разбить на части так, чтобы можно было применить уже известные формулы.

С помощью определенного интеграла можно найти длину дуги для кривой с ограничениями по формуле .

Пусть тело получено вращением криволинейной трапеции , , , вокруг оси . В этом случае поперечными сечениями будут круги с радиусами, равными , имеющими площадь .

Объем полученного тела вращения находится по формуле:

.

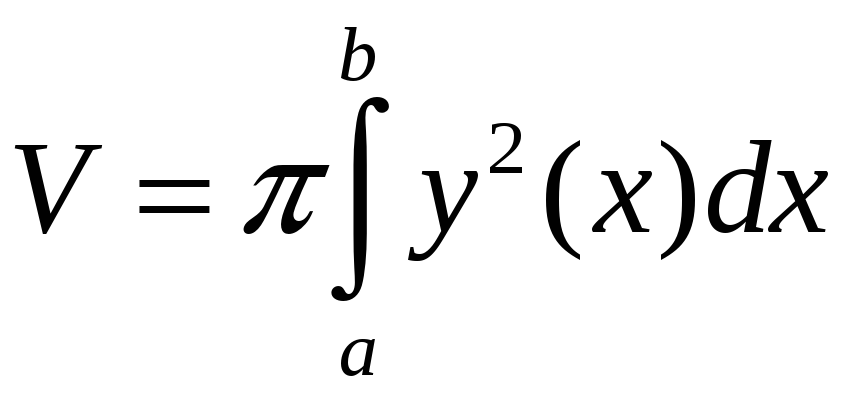Например, найти объем тела, образованного вращением эллипса вокруг оси . Так как эллипс симметричен относительно осей координат, то достаточно найти половину искомого объема. По формуле для нахождения объема тела вращения вокруг оси имеем:

.

Тогда искомый объем (куб. ед. изм.).

Также можно найти с помощью определенного интеграла площадь поверхности указанного тела вращения по формуле:

.

8.4. Применение определенного интеграла

при решении экономических задач

Рассмотрим некоторые примеры приложений определенного интеграла в экономике.

Пример 1. Найти дневную выработку за восьмичасовой рабочий день, если производительность труда в течение дня менялась по формуле , где – время в часах, – объем продукции, выпускаемой в час.

Решение. Предполагая, что производительность в течение рабочего дня меняется непрерывно от времени работы на отрезке [0, 8], дневную выработку можно выразить определенным интегралом:

В общем случае, если требуется по данной производительности труда вычислить количество произведенной продукции за время от до , применяют формулу:

.

Пример 2. Определить количество прибыли по данной отзывчивости производства , если инвестиции изменяются в пределах от до .

Решение. Отзывчивость производства на инвестиции есть производная от прибыли по вложенным средствам , то есть , следовательно, . Интегрируя это равенство на отрезке , получим , .

Итак, при внесении инвестиций в пределах от до количество прибыли равно определенному интегралу от отзывчивости производства на отрезке .

Пример 3. Пусть функция указывает, какая -я часть самых бедных людей общества владеет f(x )-ой частью всего общественного богатства. Если бы распределение богатства было равномерным, то график функции шел бы по диагонали квадрата.

Чем больше площадь заштрихованной части, тем неравномерно распределено богатство в обществе. Величина этой площади, деленная на половину площади квадрата, называется коэффициентом Джинни.

Найти коэффициент Джинни распределения богатства в обществе, если функция .

Решение. Выполним чертеж

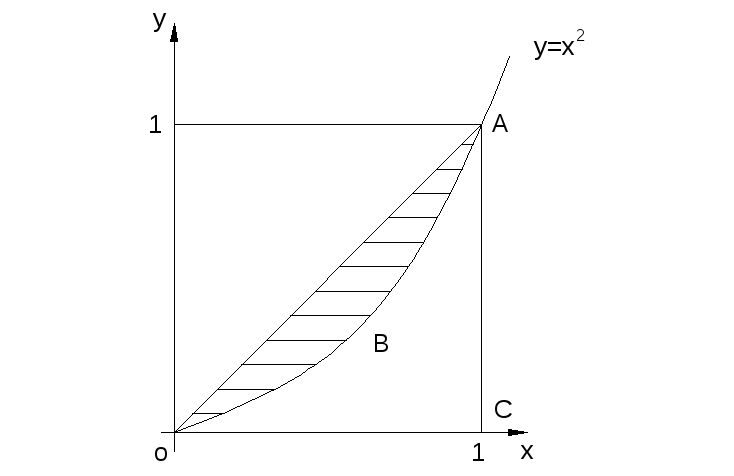
Коэффициент Джинни будет равен:

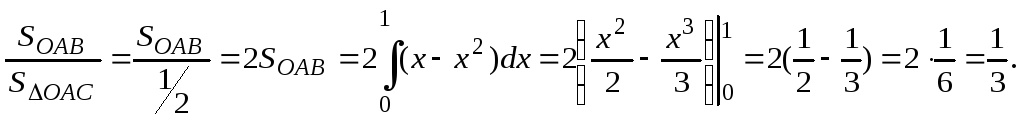
8.5. Несобственные интегралы

Обобщим понятие определенного интеграла на случай бесконечной области интегрирования. Функция непрерывна на бесконечном интервале . Поэтому на любом отрезке , где существует интеграл , который, если , имеет предел, равный единице. Этот предел называется несобственным интегралом с бесконечной верхней границей от функции и обозначается символом . Таким образом,

.

Несобственные интегралы с бесконечными пределами интегрирования называются несобственными интегралами I рода.

Несобственные интегралы I рода от функции f(x) обозначаются символами:

и определяются равенствами:

,

,

.

Если указанный предел существует и конечен, то несобственный интеграл называется сходящимся; если же предел не существует или равен бесконечности, – расходящимся.

Например, вычислить несобственный интеграл .

Имеем

.

Предел не существует, следовательно, несобственный интеграл расходится.

Для функции и непрерывной на бесконечном интервале несобственный интеграл , если он существует, можно трактовать как площадь бесконечной криволинейной трапеции, ограниченной кривой , интервалом и прямой .

В теории вероятностей рассматривается несобственный интеграл , называемый интегралом Эйлера-Пуассона. Тогда площадь под кривой (кривая Гаусса) на интервале равна единице.

В экономике с помощью несобственного интеграла можно рассчитать объем потребления, если известна функция потребления при непрерывном времени потребления.

Пусть подынтегральная функция является неограниченной на отрезке интегрирования, то есть имеет точку разрыва или на концах отрезка или внутри отрезка интегрирования. Например: , где функция имеет разрыв в точке ; , где подынтегральная функция имеет разрыв в той же точке. В этом случае определяются несобственные интегралы II рода.

Несобственные интегралы II рода обозначаются так же, как и определенные интегралы, и определяются равенствами:

, если – единственная точка разрыва функции f(x) на отрезке ;

, если – единственная точка разрыва функции f(x) на отрезке ;

, если функция f(x) имеет разрыв в точке отрезка и непрерывна для значений и .

Если предел, стоящий в правой части равенств, существует и конечен, то несобственный интеграл II рода называется сходящимся; если же предел не существует или равен бесконечности, – расходящимся. Например, вычислить несобственный интеграл . Имеем

,

то есть несобственный интеграл является расходящимся.

Контрольные вопросы

1. Что такое определенный интеграл?

2. Каковы основные свойства определенного интеграла?

3. Запишите формулу Ньютона-Лейбница.

4. Как проводится замена переменной в определенном интеграле?

5. Напишите формулу интегрирования по частям в определенном интеграле.

6. Каков геометрический смысл определенного интеграла?

7. Как определяется объем тел вращения с помощью определенного интеграла?

8. Приведите примеры использования определенного интеграла при решении экономических задач.

9. Что такое несобственный интеграл?