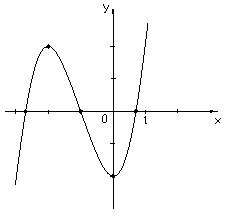Уч. пос. 2012 стр. 54-61
.doc60 61
![]() .
.
2. Определяем точки, в которых вторая
производная равна нулю![]() ,
т.е.
,
т.е.
![]()
![]() или
или
![]() .
.
3. На числовой оси отмечаем найденные точки, определяем знак второй производной на каждом из полученных промежутков:
![]()
Получаем, что для значений
![]() функция
выпукла вниз, а на интервале
функция
выпукла вниз, а на интервале
![]() функция выпукла вверх. Точки
функция выпукла вверх. Точки
![]() и
и
![]() являются точками перегиба.
являются точками перегиба.
4. Находим значения данной функции в
точке перегиба
![]() ,
,
![]() .
.
Отметим, что функция
![]() выпукла вверх на всей числовой прямой,
так как
выпукла вверх на всей числовой прямой,
так как![]() для всех значений
для всех значений
![]() .
Функция
.
Функция
![]() выпукла вниз на всей числовой прямой,
так как
выпукла вниз на всей числовой прямой,
так как
![]() для любых
для любых
![]() .
.
6.4. Асимптоты графика функции и их нахождение
Может оказаться, что график функции
неограниченно приближается к некоторой
прямой линии. Эта прямая называется
асимптотой графика функции. Так две
ветви гиперболы графика функции![]() неограниченно приближаются к осям
координат. Различают вертикальные,
горизонтальные и наклонные асимптоты.
неограниченно приближаются к осям
координат. Различают вертикальные,
горизонтальные и наклонные асимптоты.
Если хотя бы один из
односторонних пределов функции
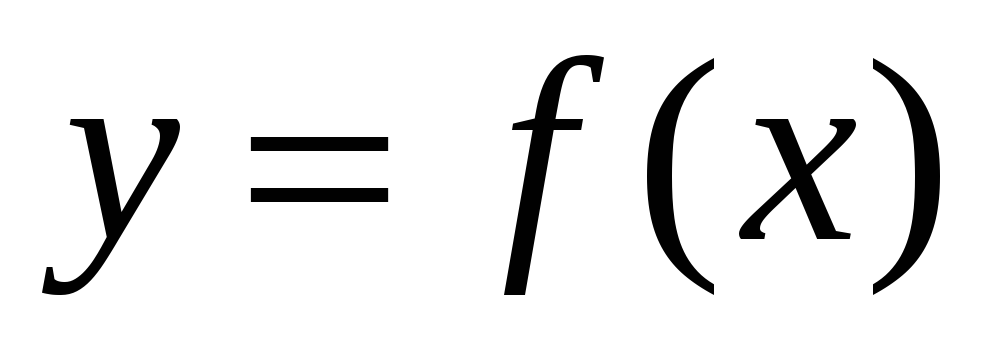 при
при
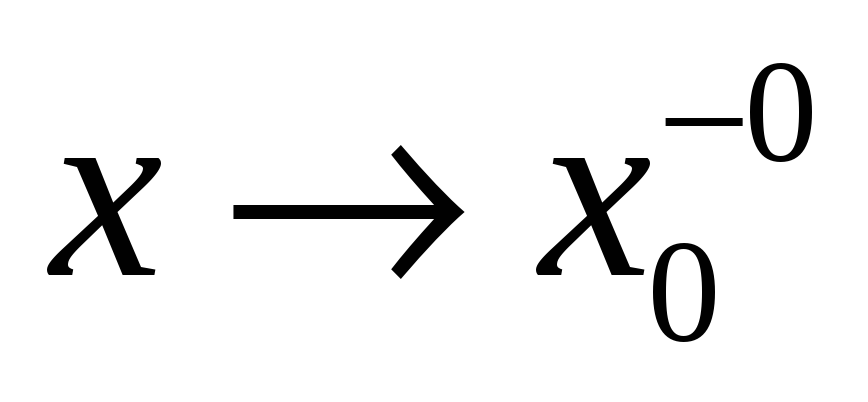 (слева) или при
(слева) или при
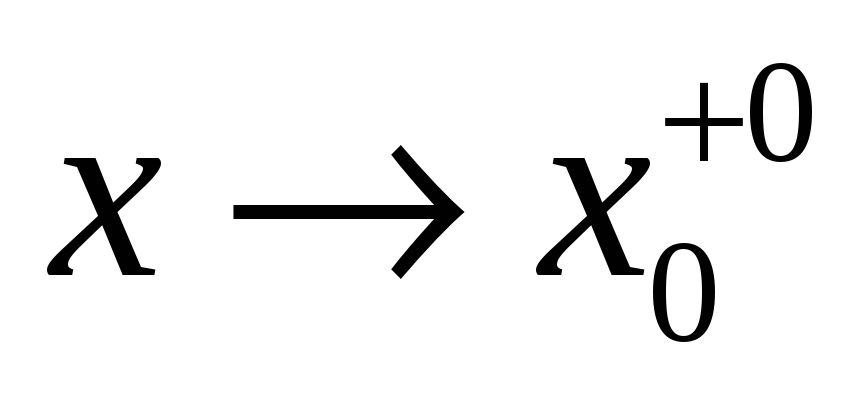 (справа) будет равен бесконечности,
т.е.
(справа) будет равен бесконечности,
т.е.
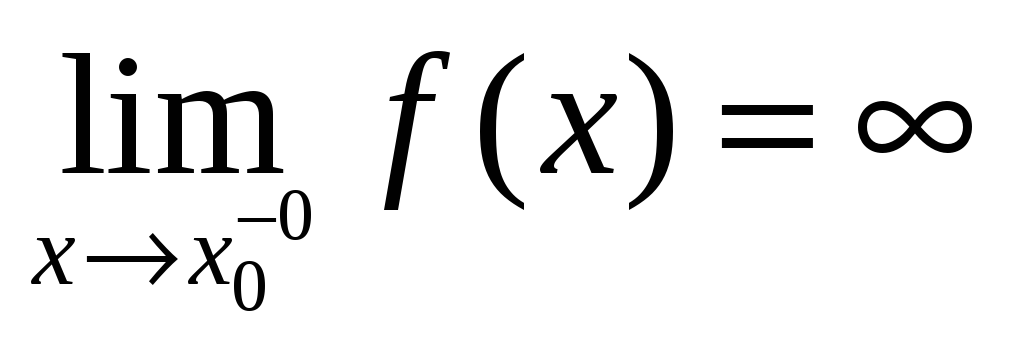 или
или
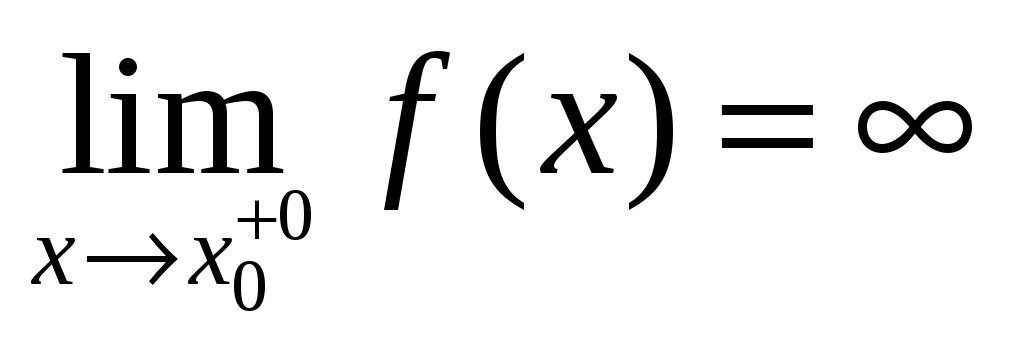 ,
то прямая
,
то прямая
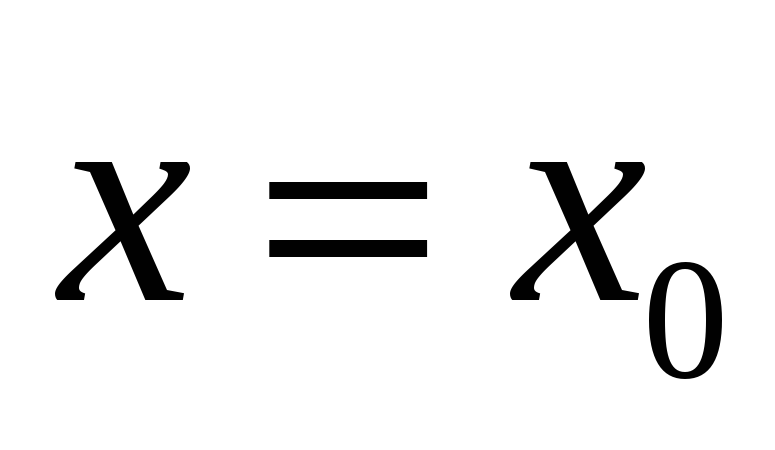 называется вертикальной асимптотой
графика функции
называется вертикальной асимптотой
графика функции
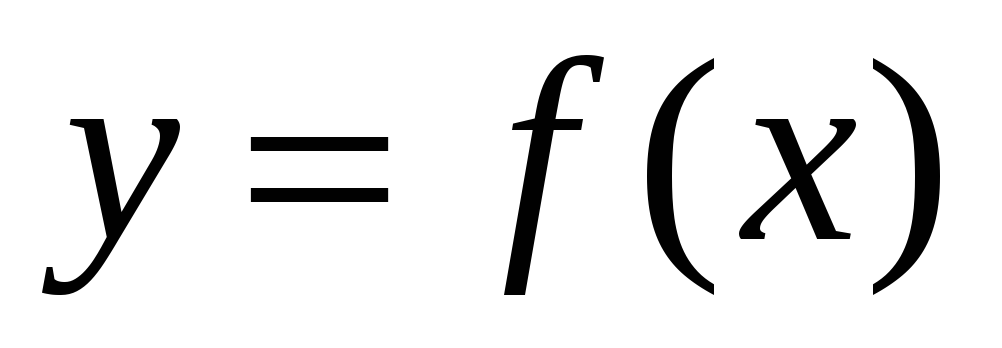 .
.
Ясно, что прямая
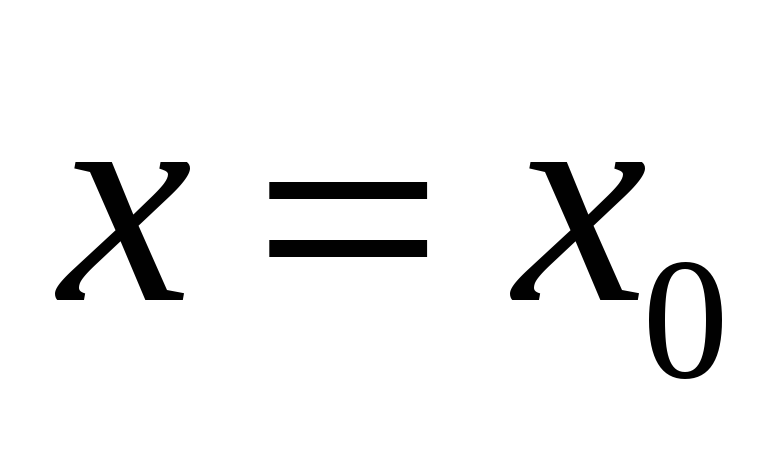 не может быть вертикальной асимптотой,
если функция непрерывна в точке
не может быть вертикальной асимптотой,
если функция непрерывна в точке
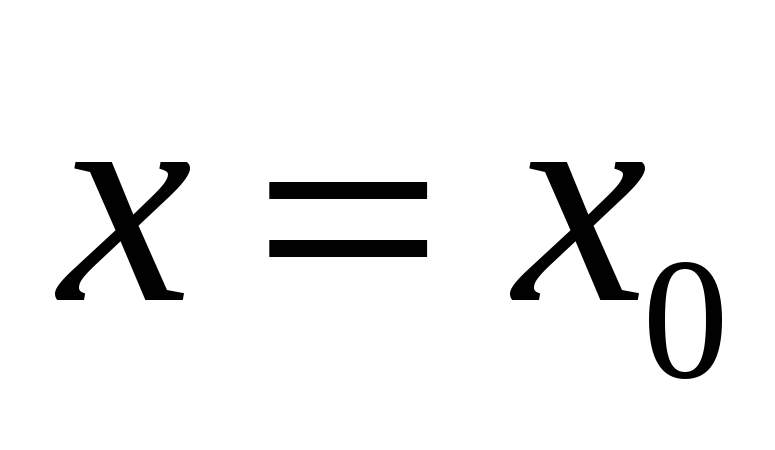 ,
так как в этом случае
,
так как в этом случае
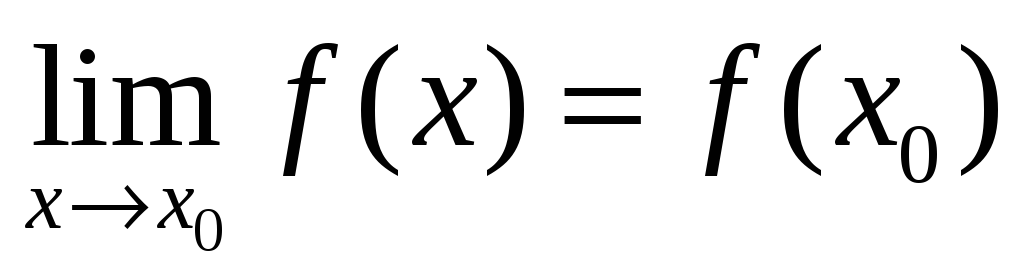 .
Следовательно, вертикальные асимптоты
следует искать в точках разрыва функции
.
Следовательно, вертикальные асимптоты
следует искать в точках разрыва функции
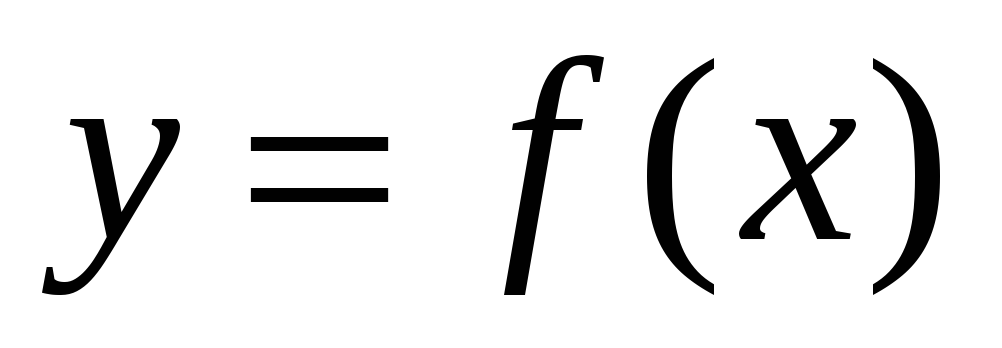 или на концах ее области определения.
Например, для функции
или на концах ее области определения.
Например, для функции
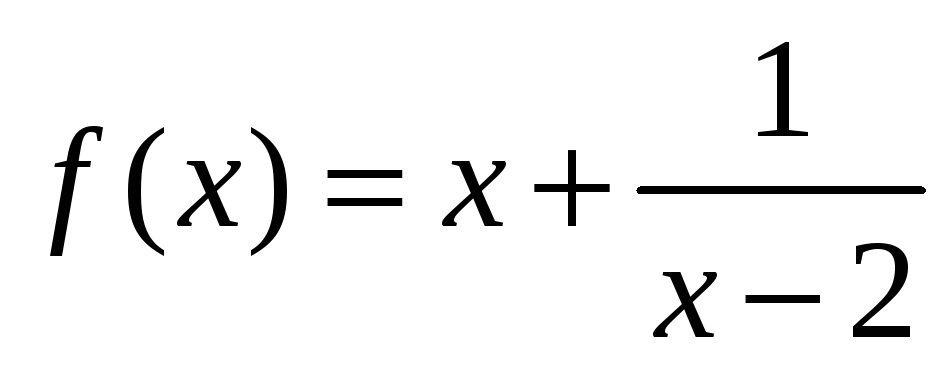 точка
точка
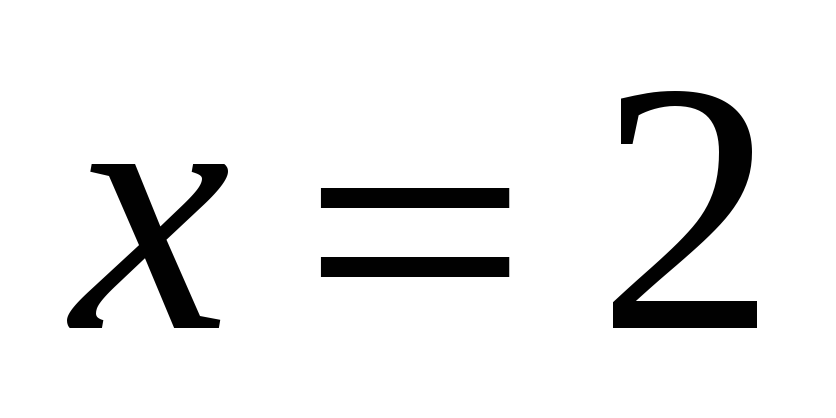 является точкой разрыва, также имеем
является точкой разрыва, также имеем
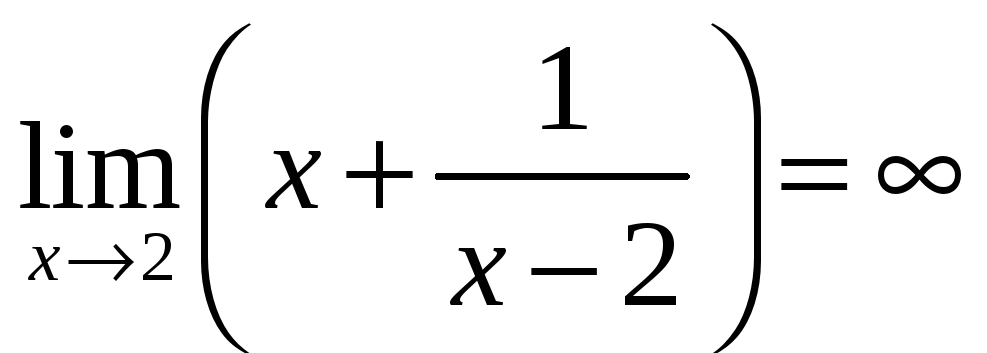 .
Итак, прямая
.
Итак, прямая
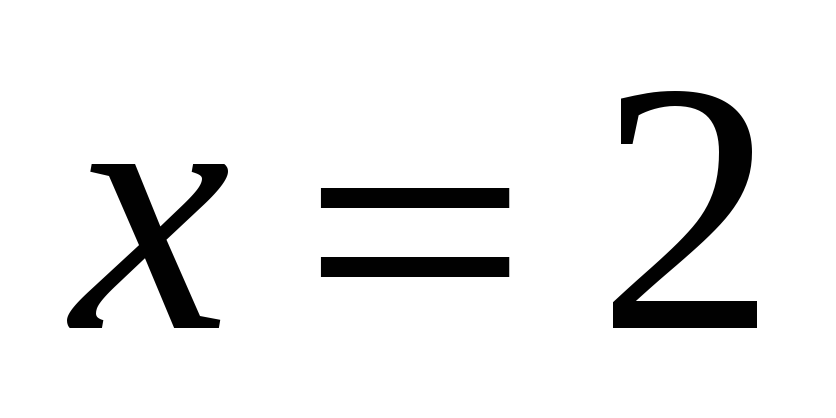 есть вертикальная асимптота.
есть вертикальная асимптота.
Если существует
конечный предел функции
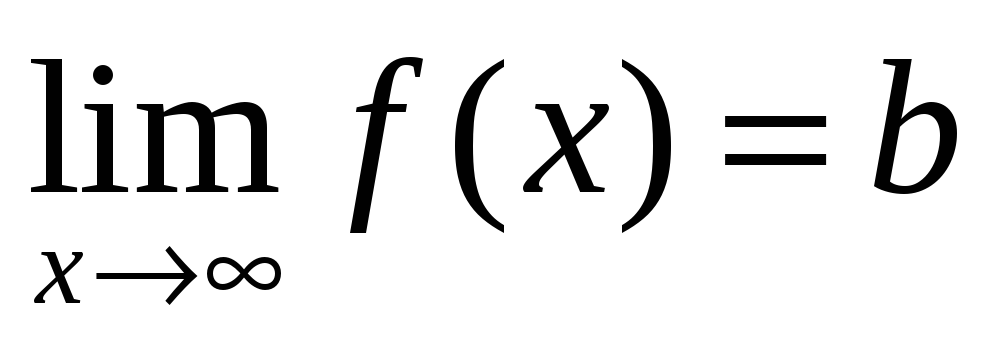 ,
тогда прямая
,
тогда прямая
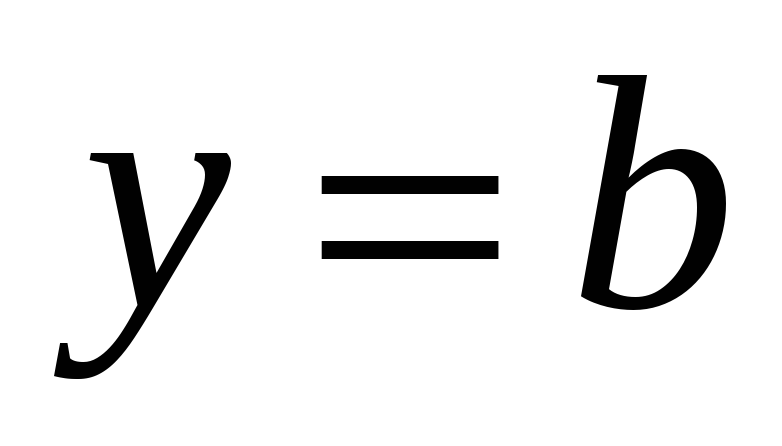 есть горизонтальная асимптота графика
функции
есть горизонтальная асимптота графика
функции
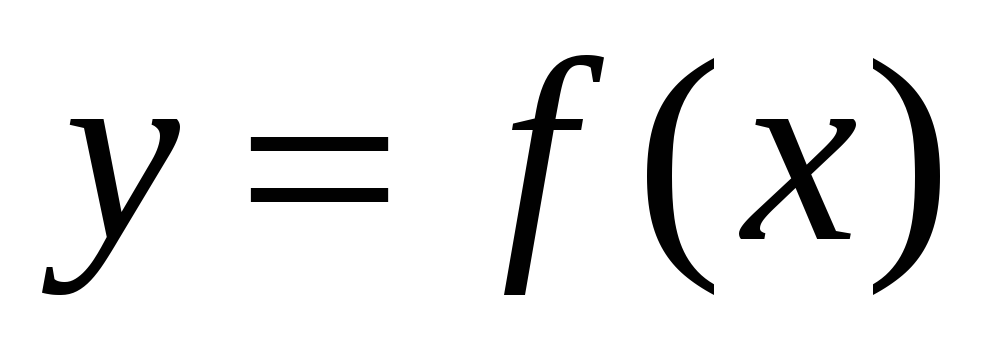 .
Если конечен только один из пределов
.
Если конечен только один из пределов
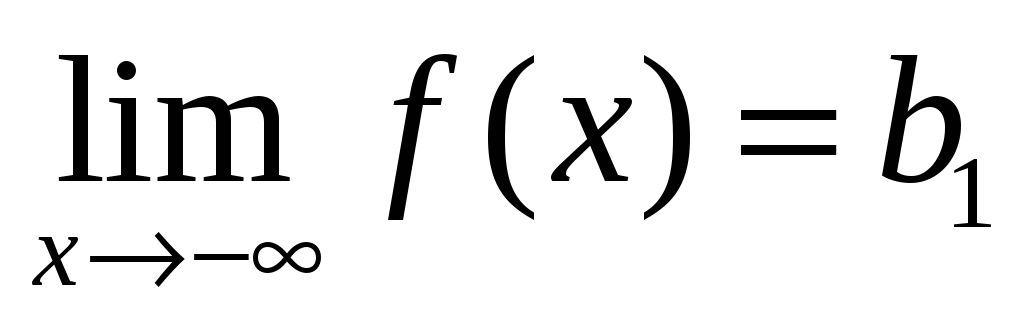 или
или
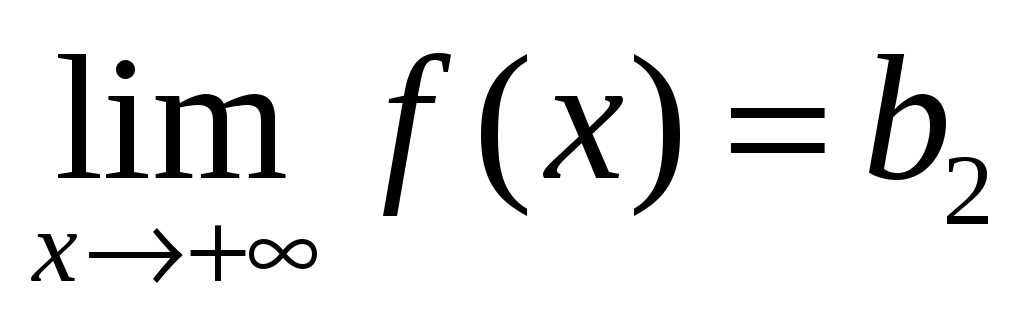 ,
то функция имеет лишь левостороннюю
,
то функция имеет лишь левостороннюю
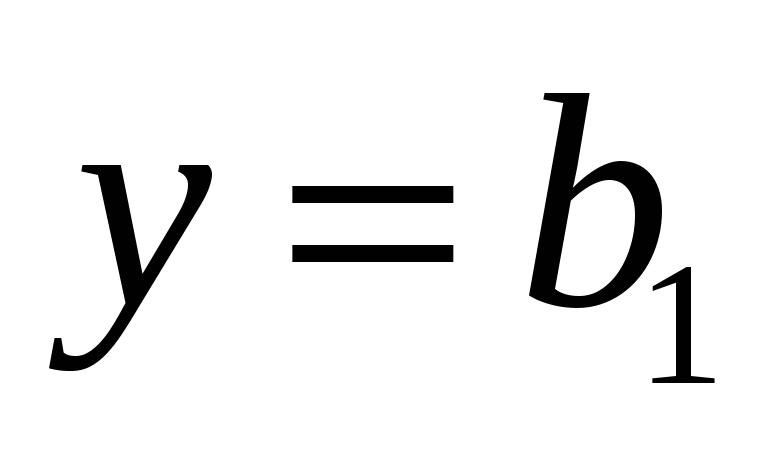 или правостороннюю
или правостороннюю
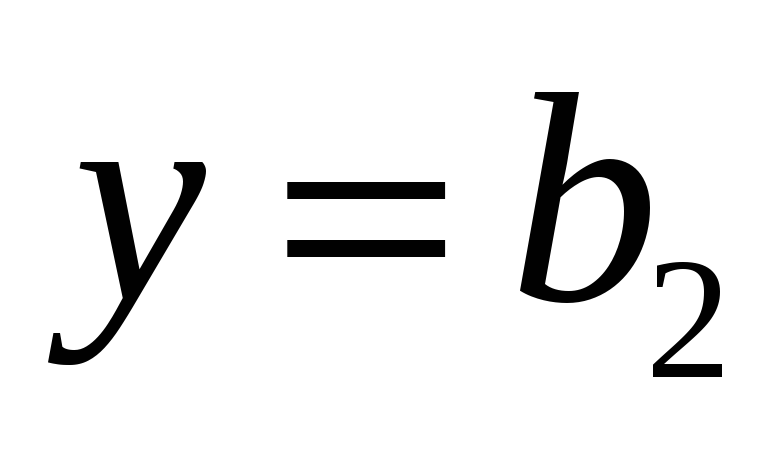 горизонтальную асимптоту.
горизонтальную асимптоту.
В случае если
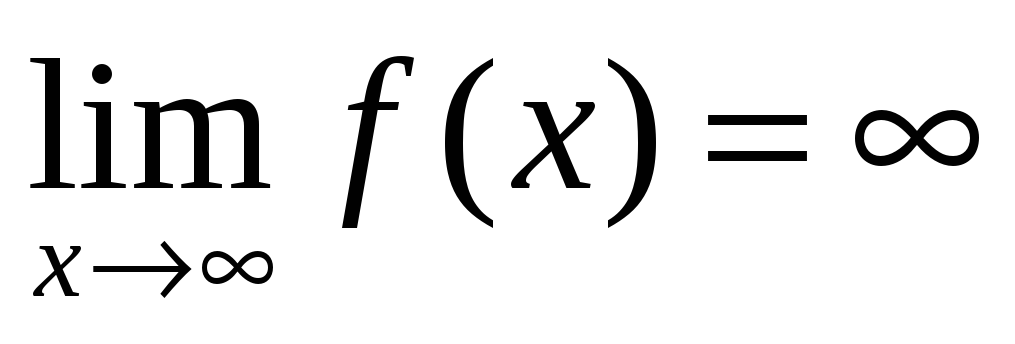 ,
функция может иметь наклонную асимптоту.
Если существует конечный предел
,
функция может иметь наклонную асимптоту.
Если существует конечный предел
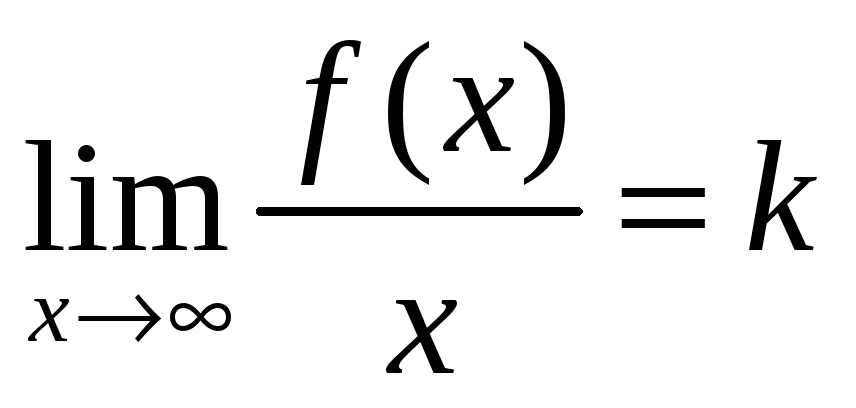 и
и
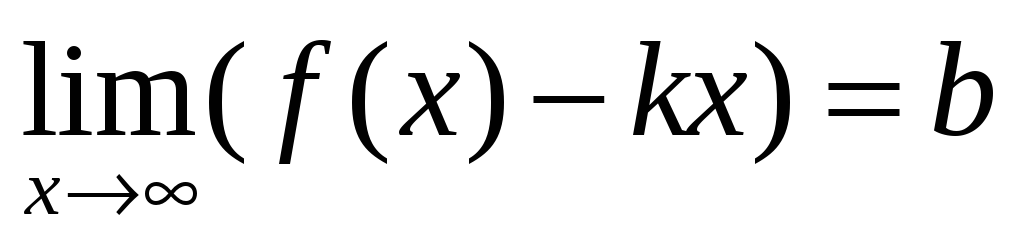 ,
тогда прямая
,
тогда прямая
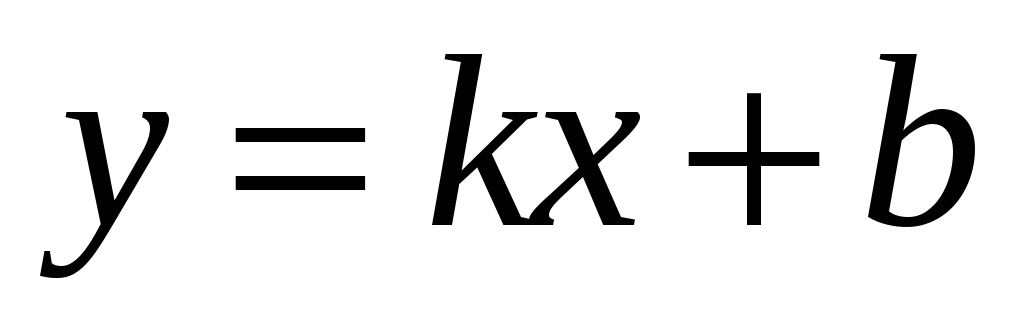 является наклонной асимптотой графика
функции
является наклонной асимптотой графика
функции
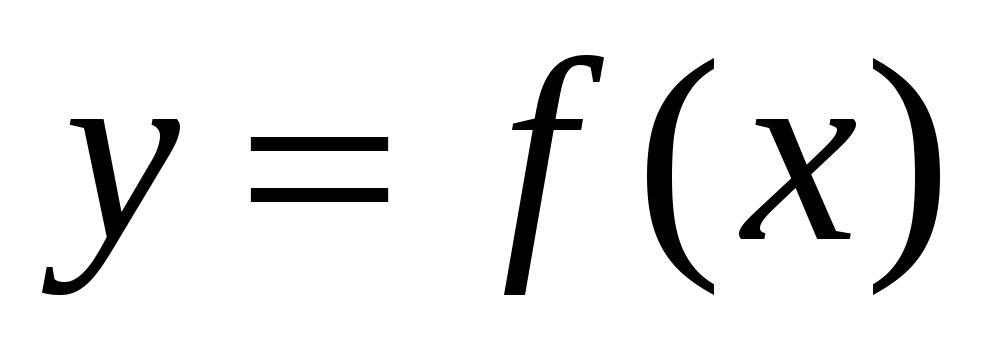 .
Наклонная асимптота может быть
правосторонней и левосторонней. Например,
найдем асимптоты графика функции
.
Наклонная асимптота может быть
правосторонней и левосторонней. Например,
найдем асимптоты графика функции
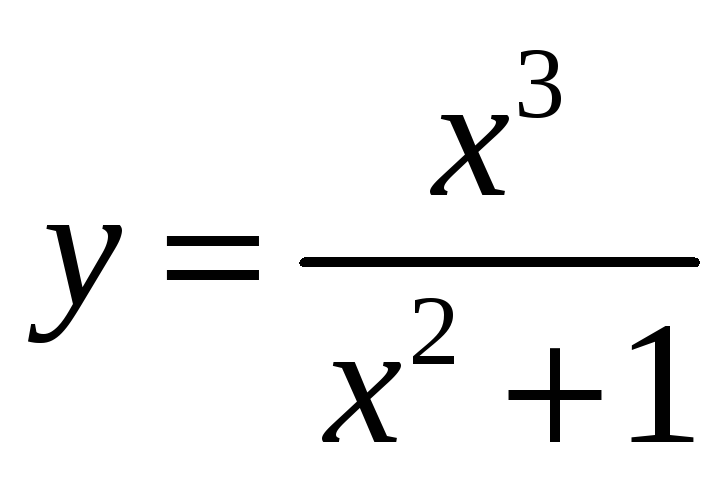 .
Областью определения функции является
вся числовая прямая, поэтому точек
разрыва и вертикальных асимптот нет.
Предел
.
Областью определения функции является
вся числовая прямая, поэтому точек
разрыва и вертикальных асимптот нет.
Предел
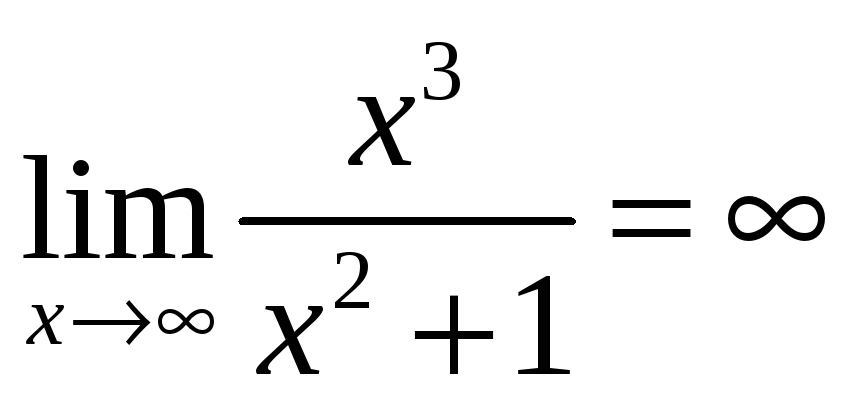 ,
т.е. горизонтальных асимптот нет. Найдем
предел
,
т.е. горизонтальных асимптот нет. Найдем
предел
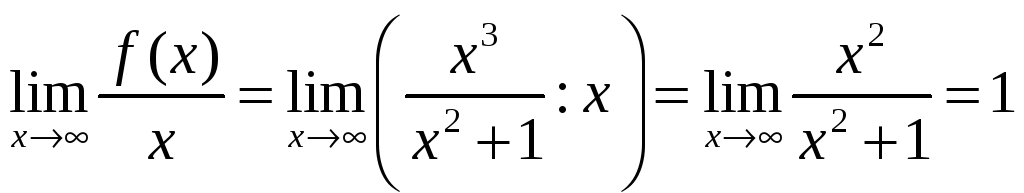 .
Итак,
.
Итак,
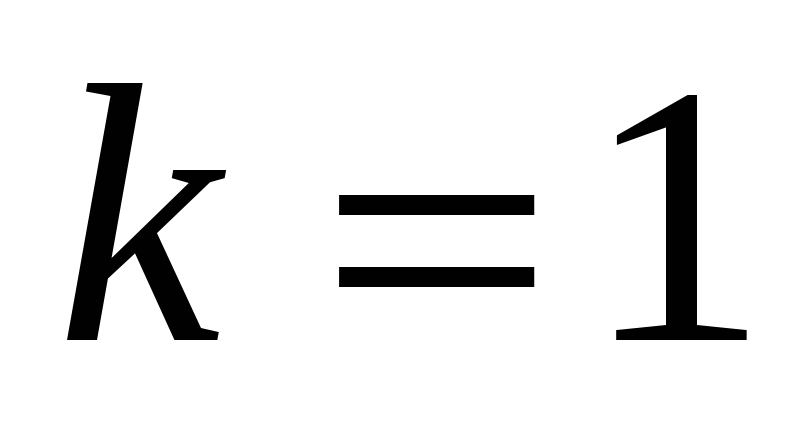 .
Находим
.
Находим
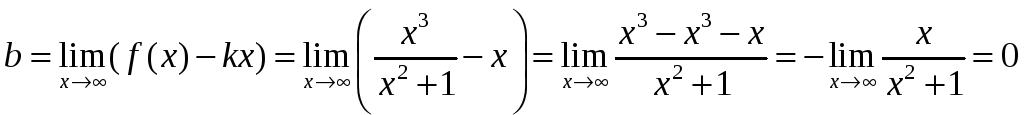 .
Таким образом, прямая
.
Таким образом, прямая
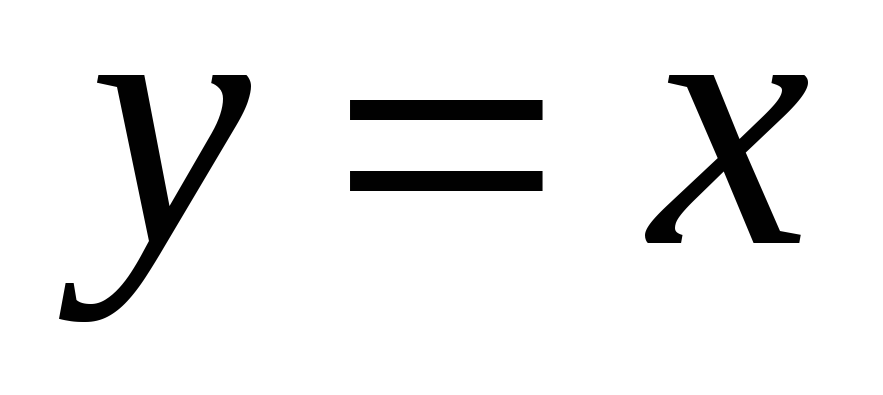 является наклонной асимптотой графика
данной функции.
является наклонной асимптотой графика
данной функции.
6.5. Схема исследования функции
и построение ее графика
Исследование заданной функции и построение ее графика производится по следующей схеме:
1) найти область определения функции;
2) определить, является ли функция четной или нечетной, периодической;
3) найти точки разрыва функции (и провести их классификацию, если требуется);
4) найти асимптоты графика функции или убедиться в их отсутствии;
5) найти точки пересечения графика функции с осями координат;
6) найти первую производную, определить промежутки возрастания и убывания функции и найти точки возможного экстремума;
7) найти производную второго порядка, промежутки выпуклости графика функции и точки перегиба;
8) построить график функции, учитывая исследование.
Заметим, что пункты схемы можно менять местами. Так, пятый пункт можно выполнять после второго пункта или седьмого.
Точки пересечения графика функции с осью абсцисс вместе с точками разрыва разбивают область определения функции на промежутки знакопостоянства.
В
тех случаях, когда функция является
четной или нечетной, достаточно
исследовать функцию и построить её
график при положительных значениях
аргумента, принадлежащих области
допустимых значений. При отрицательных
значениях аргумента график достраивается
на том основании, что для четной функции
он симметричен относительно оси
![]() ,
а для нечетной относительно начала
координат.
,
а для нечетной относительно начала
координат.
В экономике для определения тенденции роста производства предметов потребления, используют функцию
![]()
График этой функции называется логистической кривой.
Пример 1. Исследовать функцию
![]() и построить ее график.
и построить ее график.
Решение.
1. Функция определена для всех действительных значений точек числовой прямой.
2. Выясняем, является ли функция четной
или нечетной
![]() .
Функция не является ни четной, ни
нечетной, т.е. общего вида.
.
Функция не является ни четной, ни
нечетной, т.е. общего вида.
3. Так как область определения функции все действительные числа, то точек разрыва нет.
4. Находим пределы
![]() и
и
![]() .
Итак, функция неограниченно возрастает,
когда возрастает
.
Итак, функция неограниченно возрастает,
когда возрастает
![]() ,
и неограниченно убывает, когда
,
и неограниченно убывает, когда
![]() ,
поэтому горизонтальных асимптот нет.
Вертикальных асимптот также нет, так
как нет точек разрыва. Предел
,
поэтому горизонтальных асимптот нет.
Вертикальных асимптот также нет, так
как нет точек разрыва. Предел
![]() ,
поэтому наклонных асимптот нет.
,
поэтому наклонных асимптот нет.
5. Определяем точки пересечения с осями
координат. Имеем для значения
![]()
![]() .
Точки пересечения с осью абсцисс находим,
решив уравнение
.
Точки пересечения с осью абсцисс находим,
решив уравнение
![]() :
:
![]() ,
,
![]() .
.
6. Для нахождения промежутков возрастания
и убывания функции и точек возможного
экстремума находим первую производную
![]() .
Решая уравнение
.
Решая уравнение
![]() ,
получаем критические точки:
,
получаем критические точки:
![]() и
и
![]() .
Отмечаем эти точки на числовой прямой
и определяем знак первой производной
на полученных промежутках.
.
Отмечаем эти точки на числовой прямой
и определяем знак первой производной
на полученных промежутках.
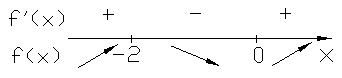
Имеем: для значений
![]() функция
возрастает, а для значений
функция
возрастает, а для значений
![]() убывает. Точка
убывает. Точка
![]() будет точкой максимума, а
будет точкой максимума, а
![]() точкой минимума. Вычисляем значения
функции в этих точках:
точкой минимума. Вычисляем значения
функции в этих точках:
![]() ,
,
![]() .
.
7. Находим вторую производную
![]() .
Вторая производная обращается в ноль,
если
.
Вторая производная обращается в ноль,
если
![]() .
Отмечаем эту точку на числовой прямой
и определяем знак второй производной.
.
Отмечаем эту точку на числовой прямой
и определяем знак второй производной.
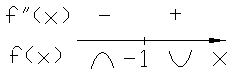
На промежутке
![]() вторая производная отрицательная –
график функции выпуклый вверх, на
промежутке
вторая производная отрицательная –
график функции выпуклый вверх, на
промежутке
![]() вторая производная положительная –
график выпуклый вниз. Точка
вторая производная положительная –
график выпуклый вниз. Точка
![]() – точка перегиба графика функции
– точка перегиба графика функции
![]() .
.
8. По результатам исследования строим
график функции. Для этого в системе
координат
![]() строим точку максимума с координатами
(-2; 2) и минимума с координатами (0; -2),
точки пересечения с осями координат и
точку перегиба. Через эти точки с учетом
промежутков возрастания и убывания
функции, а также выпуклости изображаем
график функции.
строим точку максимума с координатами
(-2; 2) и минимума с координатами (0; -2),
точки пересечения с осями координат и
точку перегиба. Через эти точки с учетом
промежутков возрастания и убывания
функции, а также выпуклости изображаем
график функции.
Контрольные вопросы
1. Каковы признаки возрастания и убывания функций?
2. Что называется экстремумом функции?
3. Как найти максимумы и минимумы функции?
4. Как найти наименьшее и наибольшее значение функции на отрезке?
5. Какая функция называется выпуклой вниз и вверх?
6. Что такое точка перегиба графика функции?
7. Как найти интервалы выпуклости функции и точки перегиба?
8. Какие асимптоты существуют для графика функции?
9. Как находятся асимптоты графика функции?
10. По какой схеме проводится исследование функций и построение их графиков?
Тема 7. Неопределенный интеграл.
Нахождение неопределенных интегралов
7.1. Первообразная функция. Неопределенный интеграл
Одной из главных задач дифференциального исчисления является задача нахождения скорости изменения какой-либо функции, то есть задача нахождения производной данной функции.
На практике, в том числе и при решении
экономических задач, часто приходится
решать обратную задачу: зная скорость
изменения функции (процесса), найти эту
функцию (закон процесса). Например,
требуется найти функцию F(x),
про которую известно, что её производная
есть некоторая функция
![]() .
Здесь,
.
Здесь,
![]() что можно проверить дифференцированием
что можно проверить дифференцированием
![]() .
Заметим, что функцию
.
Заметим, что функцию
![]() можно взять в виде
можно взять в виде
![]() где C – произвольная
постоянная (число), так как дифференцирование
постоянной величины дает ноль.
где C – произвольная
постоянная (число), так как дифференцирование
постоянной величины дает ноль.
Функция F(x)
называется первообразной функцией для
функции f(x)
на промежутке Х, если F´(x)=f(x)
в каждой точке этого промежутка. Например,
для функции
![]() первообразной будет функция
первообразной будет функция
![]()
Следующие теоремы дают ответы на вопросы, для каких функций существует первообразная функция и как отыскать все первообразные для данной функции.
Теорема 1. Любая непрерывная на
промежутке
![]() функция имеет на этом промежутке
первообразную функцию.
функция имеет на этом промежутке
первообразную функцию.
Теорема
2.
Если
функция
![]() есть
первообразная от функции
есть
первообразная от функции
![]() на
промежутке Х,
то
всякая другая первообразная от
на
промежутке Х,
то
всякая другая первообразная от
![]() отличается от
отличается от
![]() на постоянное слагаемое, то есть может
быть представлена в виде
на постоянное слагаемое, то есть может
быть представлена в виде
![]() ,
где
,
где
![]() –
постоянная.
–
постоянная.