Лабораторная работа № 15. Множественная линейная регрессия.

Цель работы. Познакомиться с режимом работы «Регрессия» для расчетов параметров множественной линейной регрессии и прогнозирования для данных значений переменных

Содержание

В пакете анализа Microsoft Excel в режиме «Регрессия» реализованы следующие этапы множественной линейной регрессии:

1. Задания аналитической формы уравнения регрессии и определение параметров регрессии

= α₀ + α₁x₁ + α₂x₂ + …+ α_mx_m,

где - теоретические значения результативного признака, полученные путем подстановки соответствующих значений факторных признаков в уравнении регрессии;

x₁, x₂,…, x_m – значение факторных признаков;

α₀, α₁,…, α_m – параметры уравнения (коэффициенты регрессии).

Эти параметры определяются с помощью метода наименьших квадратов,. то есть нахождения параметров модели (), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии.

2. Определение в регрессии степени стохастической взаимосвязи результативного признака и факторов, проверка общего качества уравнения регрессии. Здесь необходимо знать следующие дисперсии:

– общую дисперсию результативного признака , отображающую влияние как основных, так и остаточных факторов:

,

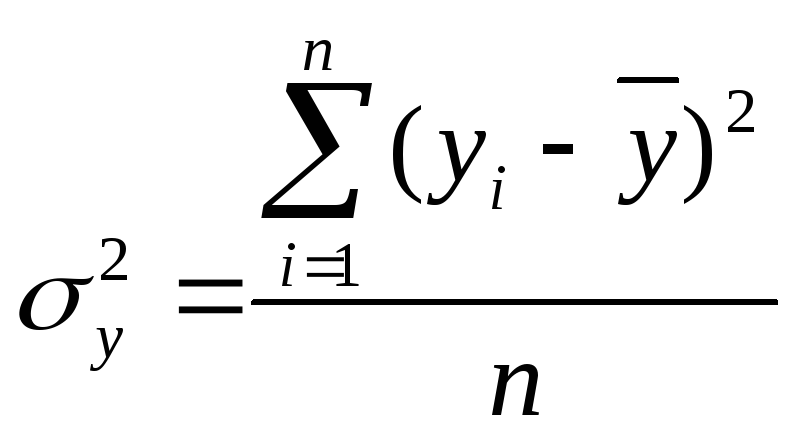где - среднее значение результативного признака ;

– факторную дисперсию результативного признака , отображающую влияние только основных факторов:

;

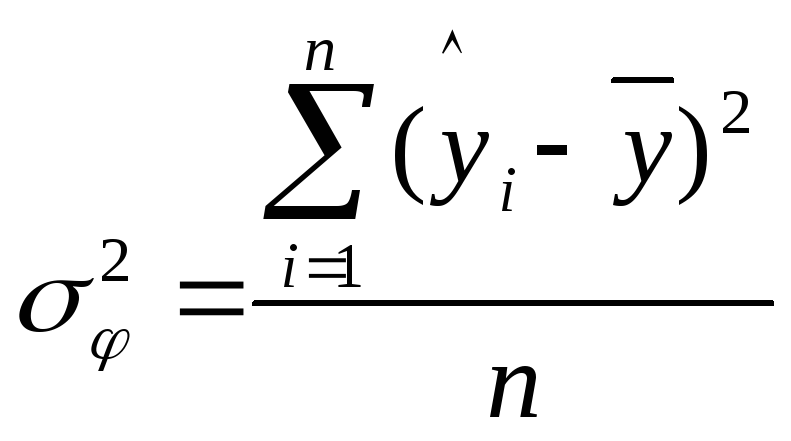– остаточную дисперсию результативного признака , отображающую влияние только остаточных факторов:

.

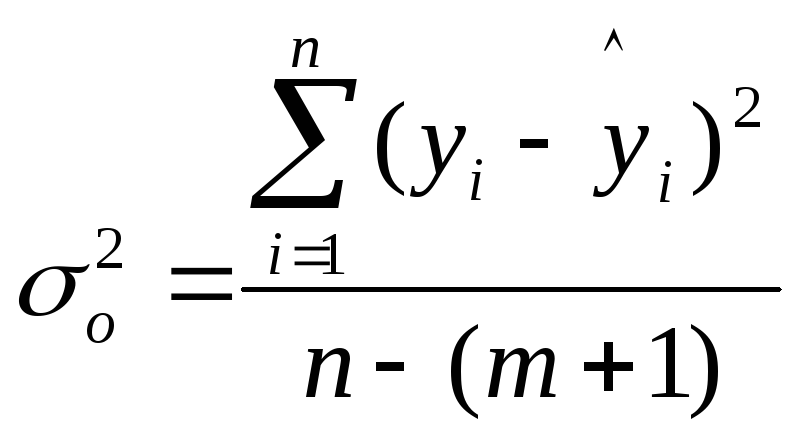При корреляционной связи результативного признака и факторов выполняется соотношение

, при этом .

Для анализа общего качества уравнение линейной многофакторной регрессии используют множественный коэффициент детерминации (квадрат коэффициента множественной корреляции ), которые рассчитываются по формуле

.

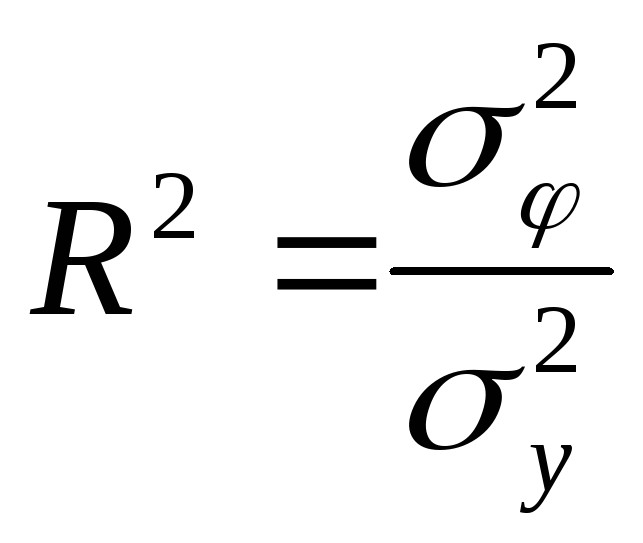Этот коэффициент определяет долю вариации результативного признака, обусловленную изменению факторных признаков, входящих в многофакторную регрессивную модель.

Так как уравнение регрессии строят на основе выборочных данных, то возникает вопрос об адекватности построенного уравнения генеральным данным. Для этого проверяется статистическая значимость коэффициента детерминации .

В математической статистике доказывается, что если гипотеза :=0 выполняется, то величина

,

имеет распределение (Фишера) с числом степеней свободы и .

При значениях >считается что вариация результативного признака обусловлена в основном влиянием включенных в регрессионную модель факторов .

Для оценки адекватности уравнения регрессии так же используют показатель средней ошибки аппроксимации:

.

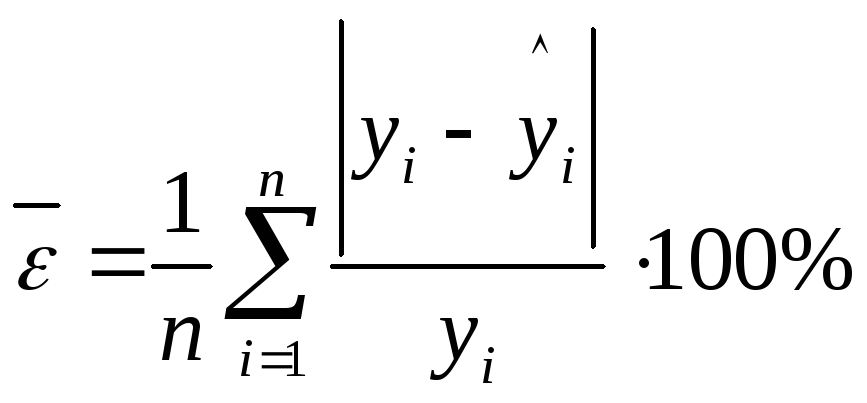3. В тех случаях, когда часть вычисленных коэффициентов регрессии не обладает необходимой степенью значимости, их исключают из уравнения регрессии. Поэтому проверка адекватности построенного уравнения регрессии включает в себя проверку значимости каждого коэффициента регрессии.

В математической статистике доказывается, что если гипотеза :=0 выполняется, то величина

,

имеет распределение Стьюдента с числом степеней свободы , где - стандартное значение ошибки для коэффициента регрессии .

Гипотеза :=0 о незначимости коэффициента регрессии отвергается, если . Зная значение можно найти границы доверительных интервалов для коэффициентов регрессии (; ).

При экономической интерпретации уравнения регрессии используются частные коэффициенты эластичности:

показывающие, на сколько процентов в среднем изменится значение результативного признака при изменении значения соответствующего факторного признака на один процент.

В диалоговом окне режима работы «регрессии» задаются следующие параметры:

1. Входной интервал – вводятся ссылки на ячейки, содержащие данные по результативному признаку (состоят из одного столбца).

2. Входной интервал – вводятся ссылки на ячейки, содержащие факторные признаки (максимальное число столбцов - 16).

3. Метки в первой строке/метки в первом столбце – устанавливаются в активное состояние, если первая строка (столбец) в обходном диапазоне содержит заголовки.

4. Уровень надежности – устанавливается в активное состояние, если необходимо ввести уровень надежности отличного от уровня 95 %, применяемого по умолчанию.

5. Константа – ноль – флажок устанавливается в активное состояние, если требуется чтобы линия регрессии прошла через начало координат ().

6. Выходной интервал/Новый рабочий лист/Новая рабочая книга – указывается, куда необходимо вынести результаты исследования.

7. Остатки – флажок устанавливается в активное состояние, если требуется включить выходной диапазон в столбец остатков.

8. Стандартизованные остатки – флажок устанавливается в активное состояние, если требуется включить выходной диапазон столбец стандартизованных остатков.

9. График остатков – флажок устанавливается в активное состояние, если требуется вывести на рабочий лист точечные графики зависимости остатков от факторных признаков .

10. График подбора – флажок устанавливается в активное состояние, если требуется вывести на рабочий лист точечные графики зависимости теоретических результативных значений от факторных признаков .

11. График нормальной вероятности – флажок устанавливается в активное состояние, если требуется вывести точечный график зависимости, наблюдаемых значений от автоматически формируемых интервалов персентилей.

Пример. Данные о прибыли предприятий , величине оборотных средств и стоимости основных фондов приведены в таблице

Номер предприятия	Прибыль , тыс. руб.	Величина оборотных средств тыс. руб.	Стоимость основных фондов тыс. руб.
1	55	47	110
2	188	129	510
3	152	87	470
4	93	69	240
5	161	102	420
6	78	64	190

По этим данным определить параметры уравнения линейной регрессии и провести их анализ.

Для решения задачи используем режим «Регрессия». На рабочем листе наберем данные:

55	47	110
188	129	510
152	87	470
93	69	240
161	102	420
78	64	190

которые вводим в режим «Регрессия». Первый столбик – значения Y, второй и третий – значения X. Указываем выходной интервал, галочкой активируем остатки и стандартные отклонения. После выполнения (ОК) получаем следующие таблицы:

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,997271
R-квадрат	0,99455
Нормированный R-квадрат	0,990917
Стандартная ошибка	5,050026
Наблюдения	6
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	2	13962,33	6981,163	273,7415	0,000402
Остаток	3	76,50828	25,50276
Итого	5	14038,83
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-1,94342	7,625418	-0,25486	0,815303	-26,2109	22,32406	-26,2109	22,32406
Переменная X 1	0,694992	0,196859	3,530397	0,038628	0,068497	1,321487	0,068497	1,321487
Переменная X 2	0,202348	0,0352	5,748573	0,010457	0,090327	0,314369	0,090327	0,314369
ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки	Стандартные остатки
1	52,97945	2,020552	0,516536
2	190,9079	-2,90787	-0,74337
3	153,6243	-1,62429	-0,41524
4	94,57447	-1,57447	-0,4025
5	153,9318	7,068209	1,806925
6	80,98213	-2,98213	-0,76235

В таблице «Регрессивная статистика» сгенерированы результаты по регрессивной статистике: множественный R коэффициент корреляции; коэффициент детерминации ; стандартная ошибка; число наблюдений n.

В таблице «Дисперсионный анализ» сгенерированы результаты дисперсионного анализа, который используется для проверки значимости коэффициента детерминации .

В следующей таблице сгенерированы значения коэффициентов регрессии и их статистические оценки. В частности первый столбец дает значения коэффициентов , и . Рассчитанные в этой таблице коэффициенты регрессии позволяют построить уравнение, выражающее зависимость прибыли предприятий Y от величины оборотных средств и стоимости основных фондов

.

Значение множественного коэффициента детерминации (из первой таблицы) показывает, что 99,5 % общей вариации результативного признака объясняется вариацией факторных признаков и . Значит, выбранные факторы существенно влияют на прибыль предприятий, что подтверждает правильность их включения в построенную модель.

В таблице «Вывод остатка» сгенерированы теоретические значения результативного признака и значения остатков. Последние вычисляются как разность между эмпирическими и теоретическими значениями результативного признака.

Сравнивая попарно коэффициенты второго и третьего столбцов третьей таблицы, видим, что абсолютные значения свободного коэффициента меньше чем его стандартная ошибка. Таким образом, свободный коэффициент следует исключить из уравнения регрессии.

Для пересчета уравнения регрессии в диалоговом окне «Регрессия» необходимо задать те же самые параметры и активировать флажок «Константа – ноль». В результате получаем аналогичные таблицы и новые уравнения регрессии:

.

В случае если незначимым является коэффициент при факторном признаке, следует пересмотреть набор признаков в уравнении регрессии.

Экономическая сущность коэффициентов и состоит в том, что они показывают степень влияния каждого фактора на прибыль предприятия. Так, например, увеличение оборотных средств на один миллион рублей ведет к росту прибыли на 0,66 миллиона рублей, увеличение основных фондов на один миллион рублей ведет к росту прибыли на 0,21 миллион рублей.