7.2 Использование для выравнивания распределения опытной информации закона распределения Вейбулла

Дифференциальную функцию или функцию плотностей вероятностей ЗРВ описывают уравнение

,

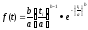где a,b – параметры ЗРВ.

Параметр bопределяют по таблице 3. Из таблицы выписывают параметрbкоэффициентыk_b иc_{b ,} предварительно посчитав коэффициент вариации.

При V=0,54;b= 1,9;k_b=0,89; С_b=0,49.

Параметр a рассчитывают по одному из уравнений

или,

Отсюда получаем

мото-ч

Дифференциальную функцию при ЗРВ определяют по таблице 5, используя уравнение

где А – длина интервала статистического ряда;

- середина интервала статистического ряда;

С – смещение начала рассеяния.

Рассчитаем значения функции во всех интервалах статистического ряда

Интегральную функцию или функцию ЗРВ определяют по уравнению

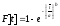
Интегральная функция приведена в таблице 6. При этом используют уравнение

Определяем значения интегральной функции во всех интервалах статистического ряда

Рассчитанные значения функций сводим в таблицу

1.4 Таблица - Значения дифференциальной и интегральной функций при ЗРВ

Интервал мотто-ч	1200-1484	1484-1768	1768-2052	2052-2336	2336-2620	2620-2904
f(t)	0,21	0,28	0,23	0,14	0,078	0,026
F(t)	0,25	0,53	0,75	0,9	0,96	0,99

На основании полученных значений f(t) иF(t) могут быть построен графики дифференциальных и интегральных функций закона распределения Вейбулла.

При построении дифференциальной кривой (рисунок 6) по оси абсцисс откладывают значение показателя надежности в определенном масштабе, а по оси ординат значение дифференциальной функции. Точки пересечения образуются значением дифференциальной функции по сои ординат и значением середины i-го интервала по оси абсцисс.

Рисунок 6. Дифференциальная кривая

При построении интегральной кривой (рисунок 7) по оси абсцисс откладывают значение показателя надежности в определенном масштабе, а по оси ординат значением интегральной функции.

Рисунок 7. Интегральная кривая

Определим число двигателей, потребующих ремонта в интервале наработки от 1700 – 2200 мото-ч.

Решение:

- по дифференциальной функции:

.

= 0,4∙29≈ 12 двиг.

- по интегральной функции

= 0,38∙29≈ 12 двиг.

8 Оценка совпадения опытного и теоретического законов распределения показателей надежности по критерию согласия Пирсона

Критерий согласия Пирсона определяется по уравнению:

,

где n_у – число интервалов в укрупненном статистическом ряду,

m_i –опытная частота,

m_Ti – теоретическая частота.

,

где N–общее количество испытанных двигателей,

интегральные функцииi-го иi-1 интервалов статистического ряда.

Для определения строят укрупненный статистический ряд, соблюдая условие:

При этом допускается объединение соседних интервалов, в которых .

Таблица 3 –Укрупненный статистический ряд

Теоретические частоты, например, в первом и втором интервалах при ЗНР определяют следующим образом:

Инт. Мото-ч.		1200-1484		1484-1768	1768-2052		2052-2336		2336-2620		2620-2904
Опытная частота		8		6	9		2		3		1
При ЗНР	F(t)	0,21	0,46		0,74	0,91		0,98		1,00
		6,1	7,25		8,12	4,93		2,03		0,58
При ЗРВ	F(t)	0,25	0,53		0,75	0,9		0,96		0,99
		7,25	8,12		6,38	4,35		1,74		0,87

= 29(0,21-0)= 6,1

= 29(0,46-0,21)= 7,25

= 29(0,74-0,46)= 8,12

= 29(0,91-0,74)= 4,93

= 29(0,98-0,91)= 2,03

= 29(1,00-0,98)= 0,58

Теоретические частоты при ЗРВ:

= 29(0,25-0)= 7,25

= 29(0,53-0,25)= 8,12

= 29(0,75-0,53)= 6,38

= 29(0,9-0,75)= 4,35

= 29(0,96-0,9)= 1,74

= 29(0,99-0,96)= 0,87

Критерий согласия Пирсона:

-при законе нормального распределения:

-при законе распределения Вейбулла:

Принимаем ЗНР, т.к =3,41, что меньше=3,91 при ЗРВ. Кроме того, пользуясь критерием согласия и приложением 9, определяем вероятность совпадения теоретического закона с опытным распределением показателя надежности. Для входа в таблицу, необходимо определить номер строки:

,

где -число интервалов в укрупненном статистическом ряду,

- число обязательных связей

N=6-3=3

Вероятность совпадения ЗНР составляет около 34%, вероятность совпадения при ЗРВ около 27%. Критической вероятностью совпадения принято считать P=10%. ЕслиP<10%, то выбранный закон следует считать недействительным.