
- •Расчетная работа
- •«Методика обработки отказов автотракторных двигателей»
- •Методика обработки полной информации
- •2. Составление статистического ряда исходной информации.
- •3. Определение среднего значения показателя надежности и среднего квадратичного отклонения.
- •398 Мото-ч.
- •4. Проверка информации на выпадающие точки
- •5 Выполнение графического изображения опытного распределения показателя надежности
- •6 Определение коэффициента вариации
- •7 Выбор теоретического закона распределения для выравнивания опытной информации
- •7.1 Использование для выравнивания распределения опытной информации закона нормального распределения
- •7.2 Использование для выравнивания распределения опытной информации закона распределения Вейбулла
- •8 Оценка совпадения опытного и теоретического законов распределения показателей надежности по критерию согласия Пирсона
- •9.1 Определение доверительных границ рассеивания при законе нормального распределения
- •Определение доверительных границ среднего значения пн при знр
- •9.2 Определение доверительных границ рассеивания при законе распределения Вейбулла
- •10 Определение абсолютной и относительной предельных ошибок переноса характеристик показателя надежности
6 Определение коэффициента вариации
Коэффициент вариации представляет собой относительную безразмерную величину, характеризующую рассеивание показателя надежности. Коэффициент вариации:
 ,
,
где C– смещение начала рассеивания показателя надежности.
При
N < 25, C
=
 -
- ;
;
При N > 25,C=
C=1200
- =
1058 мото-ч
=
1058 мото-ч
V=
7 Выбор теоретического закона распределения для выравнивания опытной информации
Для выравнивания распределения показателей надежности сельскохозяйственной техники и ее элементов наиболее широко используется закон нормального распределения (ЗНР) и закон распределения Вейбулла (ЗРВ).
В первом приближении теоретический закон распределения выбирают по коэффициенту вариации:
- при V< 0,30, выбирают ЗНР,
- при V>0,50 – ЗРВ.
Если значение коэффициента вариации находится в интервале 0,30….0,50 , то выбирают тот закон распределения, который лучше совпадает с распределением опытной информации. В нашем примере V=0,54, поэтому предварительно принимаем ЗРВ.
7.1 Использование для выравнивания распределения опытной информации закона нормального распределения
Закон нормального распределения характеризуется дифференциальной (функцией плотностей вероятностей) и интегральной (функцией распределения) функциями. Отличительная особенность дифференциальной функции - симметричное рассеивание частных показателей надежности относительно среднего значения.
Дифференциальная функция описывается уравнением

Если
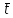 =0 и
=0 и ,
то получим уравнение для центрированной,
нормированной дифференциальной функции.
,
то получим уравнение для центрированной,
нормированной дифференциальной функции.

Для определения дифференциальной функции через центрированную нормируемую дифференциальную функцию, используют уравнение:
f(t) =
 ,
,
где А– длина интервала,
 –
среднее квадратичное отклонение,
–
среднее квадратичное отклонение,
tci – значение серединыi-го интервала,
t– среднее значение показателя надежности.
Кроме того, следует пользоваться уравнением
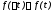
Определим значения дифференциальной функции во всех интервалах статистического ряда


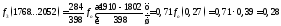



Интегральная функция (функция распределения) ЗНР определяем по уравнению:

При ti=0
и =1,00
,то получим выражение для центрированной
нормированной интегральной функции.
=1,00
,то получим выражение для центрированной
нормированной интегральной функции.

Для определения интегральной функции через центрированную нормированную функцию, используют уравнение

где
 - значение концаi-го
интервала.
- значение концаi-го
интервала.
При этом используют уравнение

Рассчитаем значения интегральной функции для всех интервалов статистического ряда






Рассчитанные значения функций сводим в таблицу
1.3 Таблица – Значения дифференциальной и интегральной функций при ЗНР
|
Интервал мотто-ч |
1200-1484 |
1484-1768 |
1768-2052 |
2052-2336 |
2336-2620 |
2620-2904 |
|
f(t) |
0,14 |
0,26 |
0,28 |
0,18 |
0,064 |
0,014 |
|
F(t)
|
0,21 |
0,46 |
0,74 |
0,91 |
0,98 |
1,00 |
На основании полученных дифференциальных и интегральных функций могут быть построены интегральные и дифференциальные кривые.
Дифференциальная кривая заменяет полигон, интегральная кривая заменяет кривую накопленных опытных вероятностей.
При построении дифференциальной кривой (рисунок 4) по оси абсцисс откладывают значение показателя надежности в определенном масштабе, а по оси ординат значение дифференциальной функции. Точки пересечения образуются значением дифференциальной функции по оси ординат и значением середины i-го интервала по оси абсцисс.

Рисунок 4 - Дифференциальная кривая
При построении интегральной кривой (рисунок 5) по оси абсцисс откладывают значение показателя надежности в определенном масштабе, а по оси ординат значением интегральной функции.

Рисунок 5 - Интегральная кривая
Определим число двигателей, потребующих ремонта в интервале наработки от 1700 – 2200 мото-ч.
Решение:
- по дифференциальной функции:
 .
.
 = 0,47∙29≈ 14 двиг.
= 0,47∙29≈ 14 двиг.
- по интегральной функции

 = 0,44∙29≈ 13 двиг.
= 0,44∙29≈ 13 двиг.
