12.Полиномиальные фильтры

Полиномиальные фильт­ры – это такие фильтры, передаточная функция которых определяется выражением

(42)

где v(p) – полином Гурвица порядка n; постоянный множитель b₀ определяет величину ослабления фильтра прототипа нижних частот (ФПНЧ) на частоте Ω=0.

По полосе частот полиномиальные фильтры разделяются на: ФНЧ, ФВЧ, ПФ и РФ.

Ослабление полиномиального фильтра (т. е. его АЧХ) является четной

функцией нормирования частоты вида

(43)

где |H(jΩ)| - модуль передаточной функции фильтра.

Если A_n-1=A_n-2=A₁=0, a A₀=A_n=1, то

(44)

Для полиномиальных фильтров Баттерворта частоту ω принято нормировать на частоте ω₀, при которой |H(jΩ)| уменьшается до 0,707 относительно максимального значения Н(0)=1. При этом A₀=1 и

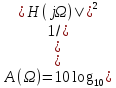(45)

Такие полиномиальные фильтры называют фильтрами с максимально плоской характеристикой или фильтрами с характеристиками Баттерворта.

Передаточная функция этих фильтров

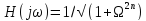(46)

Если по условиям задачи ослабление в ПП ФНЧ на его граничной частоте ω₁ не должно превышать некоторого значения ∆А, не равного 3 dB, то нормирующая частота

(47)

а ослабление ФНЧ Баттерворта

(48)

(49)

где v(s)=sⁿ+a₁s^n-1+…+a_n - полином Гурвица, а s = p/ ω_0.

Нули полинома Баттерворта рассчитываются по формулам:

при четных n

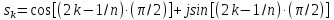(50)

при нечетных n

(51)

В формулах 50 и 51 k =1,2,3,…,2 n. Из этих 2 n значений надо выбрать те n значений, для которых s_k имеют отрицательные вещественные части.

Произведение сомножителей (s-s_k),соответствующие всем s_k с отрицательными вещественными частями, образуют полином v(s):

v(s)=П(s-s_k) (52)

На основе использования формул 50 и 51 составлена таблица 1 коэффициентов полиномов Баттерворта для n=2-7.

Таблица 1.

n	а1	а2	а3	а4	а5	а6
2	1,4142	-	-	-	-	-
3	2,0000	2,0000	-	-	-	-
4	2,6131	3,4142	2,6131	-	-	-
5	3,2361	5,2361	5,2361	3,2361	-	-
6	3,8637	7,4641	9,1461	7,4641	3,8637	-
7	4,4940	10,0978	14,5918	14,5918	10,0978	4,4940

При расчете полиномиального ФНЧ вначале следует определить порядок n фильтра-прототипа нижних частот по одной из следующих формул:

а) для фильтра с плоской характеристикой в ПП (фильтра Баттерворта)

(53)

б) для фильтра с равномерно-колебательной характери­стикой в ПП (фильтр Чебышева)

(54)

где ∆А - максимально допустимое ослабление в полосе пропускания;

A_s- минимально допустимое ослабление в полосе задерживания;

Ω_s= f_s/f₁ -нормированная частота ФНЧ на границе полосы задерживания.

Значения n, полученные по этим формулам, должны быть округлены до ближайшего большего целого числа.

В формулах (53) и (54) значения нормированной частоты имеют следующие выражения:

для ФНЧ

(55)

для ФВЧ

(56)

для ПФ

(57)

для РФ

(58)

В формулах 55, 56 f₁ —граничные частоты ПП ФНЧ и ФВЧ.

(59)

k — коэффициент преобразования ширины ПП полосово­го фильтра в фильтр прототип нижних частот (ФПНЧ), f₁ и f₂ — граничные частоты ПП ПФ и РФ.

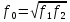(60)

f₀—средняя геометрическая частота ПФ или РФ.

Если по заданию для фильтра Баттерворта на границе ω₁ полосы его пропускания ∆А имеет значение, не равное 3 дБ, то нормирующую частоту для ФВЧ рассчитывают по формуле

(61)

Синтез двусторонне нагруженного ФНЧ Баттерворта при R_r=R_н проводится на основе формулы входного сопротивления, которая в нормированных значе­ниях имеет вид

(62)

Здесь h(s)-функция фильтрации, для фильтра Баттерворта п-го порядка она равна

(63)

Это выражение раскладывается в цепную дробь следующего вида:

(64)

которое в случае верхних знаков и в зависимости от четности или нечетности п представляет собой пару схем: рисунок 15, а и в для п нечетных, а для нижних знаков – другую пару схем: рисунок 15, б иг для п четных.

Элементы этих схем выражают собой нормированные индуктивности и емкости. Нормированные значения элемен­тов фильтров Баттерворта 2-7 порядков двусторонне нагруженных при R_r = R_H = R, рассчитанные по формуле, в результате разложения в цепную дробь приведены в таблице 2.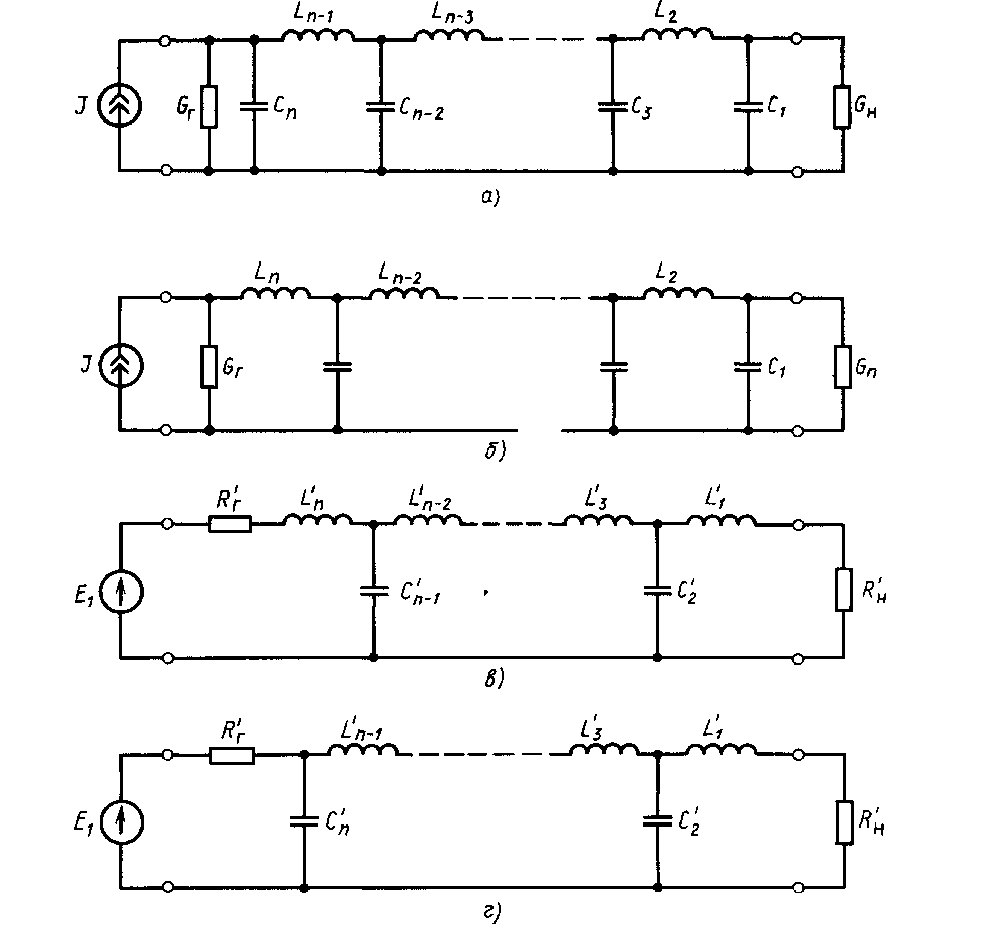

Рисунок 15 – Эквивалентные схемы ФПНЧ

Таблица 2

n	с1	l2	c3	l4	c5	l6	c7
1	2,0000	-	-	-	-	-	-
2	1,4142	1,4142	-	-	-	-	-
3	1,0000	2,0000	1,0000	-	-	-	-
4	0,7654	1,8478	1,8478	0,7654	-	-	-
5	0,6180	1,6180	2,0000	1,6180	0,6180	-	-
6	0,5176	1,4142	1,9319	1,9319	1,4142	0,5176	-
7	0,4450	1,2470	1,8019	2,0000	1,8019	1,2470	0,4450

При расчете двусторонне нагруженных фильтров Баттерворта и Чебышева при R_r = R_н для нечетных значений п и любых ∆А схемы фильтров симметричны относительно вертикальной оси, проведенной по середине фильтра, т. е. каждая половина представляет собой зеркальное отображение другой относительно этой оси.

Синтез односторонне нагруженного фильтра Баттерворта и Чебышева осуществляется образованием выражения входного сопротивления по формуле

(65)

которое раскладывается в цепную схему.

Значения элементов для нормализированного фильтра Баттерворта приведены в таблице 3[2].

Таблица 3

n	c1	l2	c3	l4	c5	l6	c7	l8	c9
1	1,0000	-	-	-	-	-	-	-	-
2	0,7071	1,4142	-	-	-	-	-	-	-
3	0,5000	1,3333	1,5000	-	-	-	-	-	-
4	0,3827	1,0824	1,5772	1,5307	-	-	-	-	-
5	0,3090	0,8944	1,3820	1,6944	1,5451	-	-	-	-
6	0,2588	0,7579	1,2016	1,5529	1,7593	1,5529	-	-	-
7	0,2225	0,6560	1,0550	1,3972	1,6588	1,7988	1,5576	-	-
8	0,1951	0,5776	0,9370	1,2588	1,5283	1,7287	1,8246	1,5607	-
9	0,1736	0,5155	0,8414	1,1408	1,4037	1,6202	1,7772	1,8424	1,5628

Расчет фильтров ВЧ и симметричных ПФ и РФ

Вначале данные этих фильтров с помощью формул преобразуются в низкочастотный прототип, порядок которого в зависимости от типа фильтра определяют по или. Затем в соответствии с таблицей 4 осуществляется преобразование нормированных элементов ФПНЧ в элементы рассчитываемого фильтра.

Из таблицы видно, что преобразование ФНЧ в ФВЧ состоит в замене нормированных элементов обратными, т. е. Ω_B=1/ Ω. Отсюда вытекает связь между любой частотой f ФНЧ и соответствующей частотой f_в ФВЧ:

(66)

Таблица 4

Нормированный элемент ФПНЧ	Преобразуется в элемент требуемого фильтра	Типы фильтров
		ФНЧ
		ФВЧ
		ПФ
		РФ

Преобразование ФНЧ в ПФ основано на симметричном преобразовании частоты, при этом индуктивные элементы преобразуются в последовательное соединение индуктивности и емкости, а емкостные — в параллельное соединение ин­дуктивности и емкости. При преобразовании ФНЧ в РФ происходит замена индуктивности параллельным соедине­нием индуктивности и емкости, а емкости — последователь­ным соединением индуктивности и емкости.

Для ПФ и РФ при задании одной частоты полосы задерживания f_1s или f_2s, другую рассчитывают по формуле[1,с. 415-417].

(67)