5.Параллельное соединение емкости и индуктивности

Если к контуру, состоящему из параллельно соединенных емкости и индуктивности, подключить переменное напряжение, то он будет представлять при его резонансной частоте очень большое сопротивление – не будет пропускать переменных токов резонансной и близких к ней частот, а все другие частоты будут встречать в нем тем меньшее сопротивление, чем дальше эта частота отстоит от резонансной.

Используя рисунок 1 и рисунок 4, построим кривую изменения реактивного сопротивления параллельного контура. При частоте f=0 проводимость Y_L=∞ и по мере увеличения f уменьшается, Y_C=0 и по мере увеличения f проводимость возрастает, стремясь к бесконечности. Общая реактивная проводимость контура является суммой реактивных проводимостей отдельных ветвей:

(15)

Кривая изменения общей реактивной проводимости контура показана на рисунке 6.

Рисунок 6 – Кривые изменения реактивных проводимостей ветвей параллельного контура и его общей реактивной проводимости в зависимости от частоты.

Характеристическое сопротивление ρ=√(L/C), резонансная частота колебательного контура, при которой Y=0 ω_p=1/√(LC). Реактивное сопротивление параллельного контура X=1/Y. график зависимости Х от частоты изображен на рисунке 7.

Рисунок 7 – Кривая изменения реактивного сопротивления X параллельного контура в зависимости от частоты.

Сопротивление, начинаясь при f=0 с нуля, с увеличением частоты, но при ω<ω_p сначала медленно, а затем все более резко возрастает в положительном направлении и при частотах, близких к резонансной, стремится к очень большим значениям, становясь в случае идеального контура равным при резонансной частоте (ω=ω_p) бесконечно большому значению. После этого оно меняет свой знак (становится отрицательным при ω>ω_p) и затем уменьшается сначала резко, а потом все медленнее, приближаясь при очень больших частотах к нулю. При низких частотах проводимость контура определяется в основном только приводимостью его индуктивной ветви, и сопротивление имеет индуктивный характер; при высоких частотах основную роль играет проводимость емкостной ветви, и потому сопротивление носит емкостный характер.

При резонансе токов в случае идеального контура сопротивления получается бесконечно большим, а ток в цепи равен нулю. В ветвях контура проходят токи

(16)

(17)

Эти токи равны и сдвинуты по фазе на 180º.

В реальном контуре контур с параллельным питанием Э.Д.С. Е должен быть приведен к эквивалентному контуру с последовательным питанием Э.Д.С. Е^’,

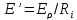(18)

где R_i – внутреннее сопротивление источника Э.Д.С.

Полное активное сопротивление эквивалентного последовательного контура будет равно

(19)

(20)

Добротность будет равна

(21)

Полное сопротивление при резонансе Z_пар реального параллельного контура определяется по формуле

(22)

6.Частотная классификация фильтров

Область частот от f=0 до f=∞ подразделяют на:

а) области, где ослабление не превышает некоторое заданное значение ослабления ∆A (полосы пропускания - ПП);

б) области, где ослабление не менее некоторого заданного значения A_s (полосы задер­живания - ПЗ);

в) переходные области.

По взаимному расположению полос пропускания и задерживания различают четыре типа фильтров:

а) фильтры нижних частот, пропускают без ослабления токи всех частот ниже некоторой предельной частоты f_гр и ослабляют токи всех частот выше частоты f_гр (ФНЧ);

б) фильтры верхних частот, пропускают без ослабления токи всех частот выше некоторой предельной частоты f_гр и ослабляют токи всех частот ниже частоты f_гр (ФВЧ);

в) полосовые фильтры, пропускают без ослабления токи определенной полосы частот от f_гр1 до f_гр2 и ослабляют токи частот ниже f_гр1 и выше f_гр2(ПФ);

г) режекторные фильтры, ослабляют токи определенной полосы частот от f_гр1 до f_гр2 и пропускают без ослабления токи частот ниже f_гр1 и выше f_гр2 (РФ).

Графически амплитудно-частотные передаточные характеристики идеальных фильтров даны на рисунке 8, а для реальных на рисунке 9 (а – ФНЧ; б – ФВЧ; в – ПФ ; г – РФ). Требования по ослаблению для всех четырех типов реальных фильтров показаны на рисунке 9. На этих рисун­ках ω₁ и ω₂ –граничные частоты полосы пропускания; ω _sl и ω _s2 — граничные частоты полосы задерживания; ∆А — не­равномерность характеристики ослабления фильтров в ПП.

Рисунок 8 – Передаточные характеристики идеальных фильтров : а) – ФНЧ, б) – ФВЧ, в) – ПФ, г) – РФ

Рисунок 9 – Требования к ослаблению фильтров

Идеальные фильтры являются физически нереализуемыми, что приводит к необходимости изменения требований к физически реализуемым фильтрам. Для этого вводят допустимые отклонения АЧХ фильтра в полосах пропускания и задерживания от АЧХ идеального фильтра, переходные полосы, расположенные между полосами пропускания и задерживания[1,с 413-414].