5.2 Определение допускаемых напряжений зубчатых колес при длительном режиме работы с постоянной нагрузкой.

Определяем допускаемые напряжения на изгиб:

[σ_F] =

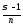
Принимаем n=1,5 - запас прочности

[σ_Fк]= 240/1,5 = 160 Мпа – для шестерни

[σ_Fш]= 400/1,5 = 266,6 Мпа – для колеса

Определяем допуск напряжений на контактную прочность

[σ_H] = 2.6 * HB

[σ_H]_Ш=650 Мпа – для шестерни

[σ_H]_k= 494 Мпа – для колеса

5.3 Расчет зубьев на изгибную прочность

Определение модуля

Как известно, наиболее нагруженной парой колёс является последняя пара, наиболее близкая к выходу. Поэтому для определения модуля зацепления зубчатых колёс следует рассмотреть сначала эту пару. При расчёте на изгибную прочность модуль определяется по формуле :

.

В этой формуле:

–для цилиндрических прямозубых колёс ;

–момент на рассматриваемом колесе;

–коэффициент расчётной нагрузки, учитывающий увеличение момента нагрузки и дефектов монтажа, , примем K=1,3 ;

–коэффициент формы зуба. Этот коэффициент выбирается в зависимости от числа зубьев.

–коэффициент ширины колеса, для мелкомодульных колёс , примем ψ_b=8;

–число зубьев колеса;

–допускаемое напряжение при расчёте на изгиб;

Теперь необходимо определить наименее прочное колесо зубчатой пары, для чего следует рассмотреть отношение

Где Y_F - Коэффициент формы зуба. Y_F

Воспользовавшись справочной литературой, получим, что для шестерни:

z = 28, Y_F = 3,96

а для колеса:

z = 100, Y_F = 3,75.

Тогда отношения для шестерни Z₅ и колеса Z₆ будут равны соответственно:

Для шестерни: 0,015

Для колеса. 0,023

Расчет следует вести по колесу, т. к. оно нагружено больше.

Момент на выходном колесе равен

ω_z6=ω_вых=2V/d=1,25 1/с

М_кр=F*V/ω_z6=160 Н*мм

Подставим все значения в формулу для определения модуля:

Получим m ≥ K_m = 1,4*

Возьмём из ряда значений ближайшее подходящее: m = 0,4

5.4 Расчет геометрических размеров

Определим геометрические параметры элементов редуктора по приведённым ниже формулам

Делительный диаметр колеса, шестерни:

Диаметр окружности вершин зубьев: m*(z+2)

Ширина обода (венца) колеса, шестерни:

Диаметр окружности впадин: m*(z-2,5)

Межосевое расстояние между колесами зубчатой пары:

.

Zi	bi, мм	d, мм	da, мм	df, мм	a
Z1=28	5,0	11,2	12	10,2	25,6
Z2=100	3,2	40	40,8	39
Z3=28	5,0	11,2	12	10,2	25,6
Z4=100	3,2	40	40,8	39
Z5=28	5,0	11,2	12	10,2	25,6
Z6=100	3,2	40	40,8	29

5.5 Проверочный расчет зубьев на контактную прочность

Выполним расчёт зубчатых колёс на контактную прочность по формуле Герца. Как уже отмечалось выше, наиболее нагруженной является последняя пара зубчатых колёс, а наименее прочным является колесо этой пары, поэтому расчёт будем проводить именно для него. Контактное напряжение, в соответствии с формулой Герца, вычисляется :

σ_н=

i₅₆– передаточное отношение между 5-м и 6-м колесами, i₅₆ = 3,4

_Мкр - момент на 6-м колесе, M = 160H*мм;

a –межосевое расстояние рассматриваемой пары a=25,6 мм

_{Для стальных прямозубых колес}

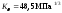
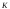–коэффициент расчётной нагрузки. K=1,3

σ_н = 291МПа < [σ_Н] (для колеса)=425 МПа

Расчет прошел.