1. Алгоритмы решения задачи для доски 8*8.
1.1Рекуррентный способ:
Постановка задачи: как на шахматной доске расположить восемь ферзей
таким образом, чтобы никакие два из них не угрожали друг другу.
Решение:
Рассмотрим шахматную доску, клетки которой помечены с помощью
системы координат следующим образом:
|
1111 1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
1пра 1 |
2222 2 |
3333 3 |
4444 4 |
5555 5 |
6666 6 |
7777 7 |
8888 8 |
Можно заметить, что два ферзя, которые находятся в клетках с координатами (x1, y1) и (x2, y2), будут бить друг друга если выполняется хотя бы одно из следующих равенств:
1) x1 = x2, то есть ферзи находятся на одной вертикали;
2) y1 = y2, то есть ферзи находятся на одной горизонтали;
3) x1+y1 = x2+y2, то есть ферзи находятся на одной диагонали, идущей
снизу вверх слева направо. Это равенство верно только для приведен-
ной нумерации клеток шахматной доски;
4) x1−y1 = x2−y2, то есть ферзи находятся на одной диагонали, идущей сверху вниз слева направо. Это равенство также верно только для приведенной нумерации клеток шахматной доски.
Алгоритм рекуррентного способа : Очевидно, что все восемь ферзей находятся на разных вертикалях шахматной доски, иначе найдутся два из них, которые бьют друг друга. Поэтому нам нужно перебрать для каждого ферзя все возможные горизонтали, где он может встать и проверить, чтобы все ферзи не были под боем. Заведем массив q, индекс которого соответствует номеру ферзя, а значение q[i] указывает на какой по счету горизонтали находится i-й ферзь.
Поскольку решение предполагает переборный алгоритм, заведем восемь переменных q1, . . . , q8, которые будут пробегать от 1 до 8 и устанавливать соответствующего ферзя на выбранную горизонталь. Например, если qi=4, это значит, что i-го ферзя необходимо поставить на 4-ю горизонталь. Зададим функцию boy(c), которая в качестве аргумента будет принимать номер ферзя и проверять, не бьют ли ферзя с номером «c» ферзи с 1-го до «c» − 1-го. Эта функция возвращает значение «истина» в случае если «c»-го ферзя бьет хотя бы один ферзь и «ложь» в противном случае.
Блок-схема алгоритма:
Реализация алгоритма на языке Pascalнаходится в приложении.
В данной программе ищутся все возможные решения задачи и выводится их число: 92. Интересно отметить, что эти 92 расположения разбиваются на 12 групп: при помощи поворотов (вращений) доски на 90, 180 и 270°, а также при ее зеркальном отражении относительно линий, разделяющих доску пополам:
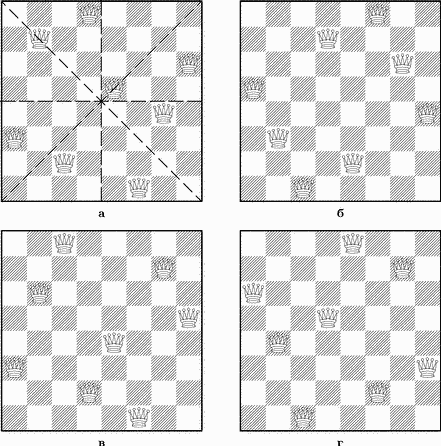
Например, из расстановки, показанной на рис. А, при повороте доски на 90° по часовой стрелке мы получаем расстановку на рис. В. А при отражении доски относительно линии, разделяющей королевский и ферзевый фланги, – на рис. Г. При помощи других поворотов и отражений доски можно получить еще пять решений. Набор расстановок восьми мирных ферзей называется основным, если, во-первых, эти расстановки не переходят друг в друга при поворотах и отражениях доски, и, во-вторых, любая другая расстановка получается из какой-нибудь основной при помощи данных преобразований доски. Доказано, что всякий основной набор решений задачи содержит ровно 12 расстановок. Вот один из таких наборов:
1) см. рис. А;
2) см. рис. Б;
3) a4, b1, c5, d8, e6, f3, g7, h2;
4) a4, b2, c5, d8, e6, f1, g3, h7;
5) a4, b2, c7, d3, e6, f8, g1, h5;
6) a4, b2, c7, d3, e6, f8, g5, h1;
7) a3, b5, c2, d8, e6, f4, g7, h1;
8) a4, b1, c5, d8, e2, f7, g3, h6;
9) a4, b7, c3, d8, e2, f5, g1, h6;
10) a6, b4, c2, d8, e5, f7, g1, h3;
11) a4, b8, c1, d5, e7, f2, g6, h3;
12) a4, b2, c7, d5, e1, f8, g6, h3.
Остальные 80 расстановок получаются из этих двенадцати при помощи поворотов и отражений доски. Основная расстановка на рис. Б является симметрической. Другие одиннадцать основных расстановок – простыми. Итак, всего на доске имеем 11·8+1·4=92 расстановки восьми ферзей, не угрожающих друг другу.