
Физпрактикум.Оптика
.pdf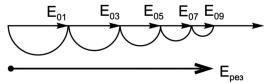
4.2. Дифракция Френеля. Метод зон |
181 |
|
|
4.2.3. Зонная пластинка
Зонная пластинка Ð это стеклянная пластинка, на поверхность которой нанесено непрозрачное покрытие в виде колец, закрывающих только четные (или только нечетные) зоны Френеля.
Если экран открывает одну зону Френеля, то результирующая амплитуда Е01 & 2Е0, а интенсивность I1 & 4I0. Но если мы будем складывать только колебания от четных или только от нечетных зон Френеля, то получим колебания с амплитудой, модуль которой намного превосходит величину E0. Действительно, вместо суммы членов знакопеременного ряда мы будем складывать значения E одного знака. Векторная диаграмма сложения колебаний представлена на (рис. 4.9).
!"#. ).1. A)7%-&*'G 4"'0&'..' #,-()*"G 7-,):'*"< 4,G 6-**-< +,'#%"*7"
Для небольшого числа зон можно считать, что Ерез= kЕ01; I = k2I1, где k Ð число открытых зон.
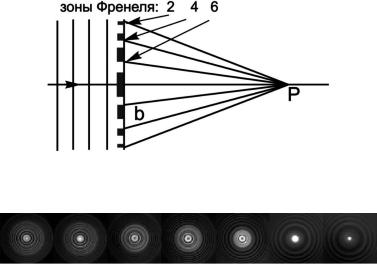
Интенсивность в точке наблюдения при использовании зонной пластинки становится во много раз больше. На рисунке 4.10 показана зонная пластинка, закрывающая нечетные зоны Френеля.
Зонная пластинка фокусирует свет аналогично собирающей линзе, только в отличие от линзы пластинка имеет несколько фокусов. Из формулы (4.4) следует, что расстояния а от пластинки до источника и b от пластинки до изображения связаны тем же соотношением, что и соответствующие величины для линзы:
1/a + 1/b = 1/F, (4.7)
где фокусное расстояние F определяется формулой F = rm2/mλ. Соотношение (4.7) Ð формула зонной пластинки.
Если на зонную пластинку падает параллельный пучок лучей (а ∞), то, как следует из соотношения (4.7), b = rm2/ mΑ = f, где f Ð главное фокусное расстояние зонной пластинки.
Если центр зонной пластинки прозрачный, то m Ð нечетное и в формулу (4.7) входит внешний радиус r светлого кольца пластинки.
182 |
Тема 4. Дифракция света |
|
|
!"#. ).#2. F-**'G +,'#%"*7'3 6'7&=/'9H'G
*)2)%*=) 6-*= I&)*),G
!"#. ).##. I-71#"&-/7' #/)%' '.+,"%14*-< 6-**-< +,'#%"*7-< +- .)&) +&":,"()*"G 7 0,'/*-.1 ?-71#1 C 0#,)/' *'+&'/-.
Если же центр пластинки непрозрачный (рис. 4.10), то под r следует понимать внешний радиус темного кольца. С помощью зонной пластинки можно даже получать оптические изображения, хотя и весьма низкого качества. В отличие от линзы, зонная пластинка имеет несколько фокусов: Fn = F/(2n + 1), где n Ð любое целое число. В главном фокусе зонной пластинки собирается около 10 % всей падающей на нее энергии (рис. 4.11), 50 % попадает на непрозрачных промежутках, 40 % Ð на побочных фокусах.
Следующим шагом в своего рода совершенствовании зонной пластинки является превращение ее в прозрачную фазовую зонную пластинку. Вместо того чтобы закрывать, например, нечетные зоны Френеля, мы можем изменять на π фазу приходящих от них колебаний. Тогда амплитуда колебаний в точке наблюдения примерно удвоится. Чтобы достигнуть этого, необходимо изменить для них оптическую длину пути на половину длины волны, обеспечить выполнение условия d(n Ð 1) = λ/2, где d Ð толщина фазовой пластины из материала с показателем преломления n.
4.2. Дифракция Френеля. Метод зон |
183 |
|
|
4.2.4. Дифракция на прямолинейном крае экрана
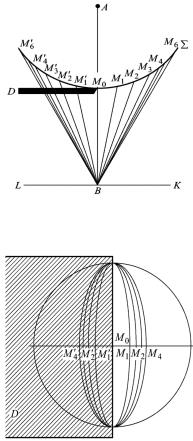
При дифракции на краю экрана или на узкой щели количественный расчет наблюдаемой картины по методу кольцевых зон Френеля неудобен, так как прямолинейный край экрана пересекает зоны. Удобней дугами разбить волновую поверхность на лунки, подобно делению поверхности Земли на пояса меридианами (рис. 4.12, 4.13). Однако расстояния между дугами уменьшаются от центра к периферии.
!"#. ).#$. !'6:")*") ?&-*%' /-,*= *' ,1*7"3 '*',-0"2*=) 6-*'. I&)*),G
0N#D & 92D 5 N$D & 9#D 5 E 5 V;$.
!"#. ).#(. O,,"+%"2)#7") 7&"/=) & +&-)73"" 0&'*"3 ,1*-7
*' +,-#7-#%8 L7&'*' <
184 |
Тема 4. Дифракция света |
В отличие от кольцевых зон, площади лунковых зон значительно отличаются друг от друга. Их площади относятся как ряд чисел:
S1 : S2 : S3 : S4 É = 1 : 0.41 : 0.32 : 0.27 : 0.23 : 0.22É
Площади зон с возрастанием номера быстро убывают, поэтому амплитуды колебаний, создаваемых в точке В лунковыми зонами Френеля, будут также быстро уменьшаться от зоны к зоне. Следует заметить,
что зоны ММ1 и ММ1 , М1М2 и М1 М2 , М2М3 и М2 М3 и т. д. (рис. 4.12, 4.13) располагаются симметрично относительно линии SВ и имеют
одинаковую площадь. Поэтому создаваемые ими в точке В колебания совпадают по амплитуде и фазе. ÒШтрихованныеÓ зоны дополняют действие зон ÒнештрихованныхÓ. Эти особенности лунковых зон неизбежно должны сказаться на построении векторной диаграммы.
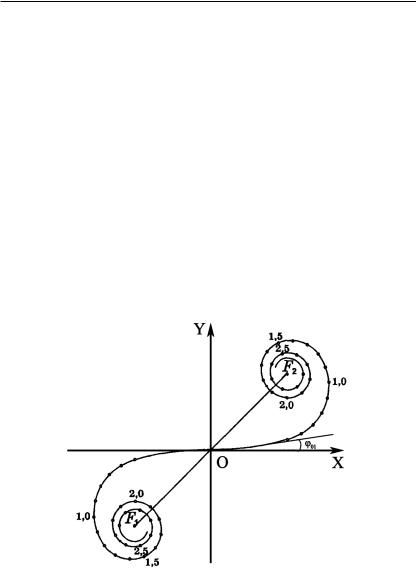
Положительная ветвь спирали соответствует ÒнештрихованнымÓ зонам, отрицательная Ð ÒштрихованнымÓ. Назовем ÒнештрихованныеÓ зоны Френеля положительными, а ÒштрихованныеÓ Ð отрицательными. Отрезок FÐF+ дает суммарную амплитуду колебания от полностью открытой волновой поверхности. Эта векторная диаграмма получила название спирали Корню (рис. 4.14).
!"#. ).#). D+"&',8 Q-&*9
4.2. Дифракция Френеля. Метод зон |
185 |
На рис. 4.14 видно, что результирующее колебание в точке F2 отличается по фазе на угол cφ = π/4 от колебания, создаваемого центральным участком (точка О волновой поверхности). Этот результат не совпадает с экспериментальными данными и является одним из недостатков теории Гюйгенса Ð Френеля. Амплитуда же по диаграмме определяется правильно в полном соответствии с экспериментом.
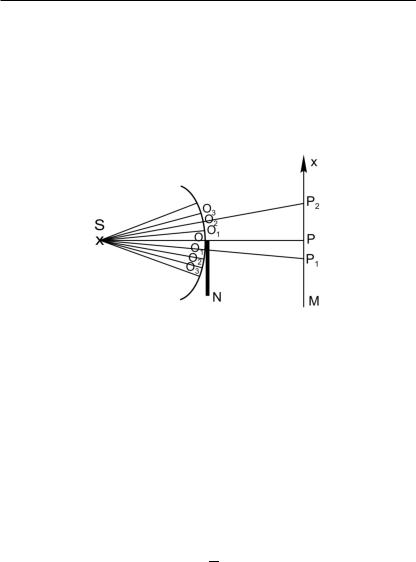
Используем спираль Корню для изучения распределения интенсивности при дифракции сферической волны на крае непрозрачного экрана N (рис. 4.15).
!"#. ).#+. ["?&'73"G #?)&"2)#7-< /-,*= *' 7&') *)+&-6&'2*-0- L7&'*'
Дифракционная картина наблюдается на экране М. Необходимо учитывать, что ÒработаютÓ только открытые зоны Френеля.
Обозначим амплитуду световых колебаний в точке Р в отсутствие экрана Е0, интенсивность I0. Известно, что I0 ~ Е02. Из рис. 4.14 следует, что Е0 = FÐF+. Для точки Р, лежащей на границе геометрической тени, все отрицательные зоны закрыты. Колебаниям от положительных зон соответствует положительная часть спирали Корню. Амплитуда колебания в точке Р будет равна:
""
;I % >( % # ((( % # ;6 +
а интенсивность
"
7I % D 76&
При смещении точки наблюдения в область геометрической тени (точка Р1) дифракционный экран N будет закрывать все большее чис-
186 |
Тема 4. Дифракция света |
ло положительных зон. Поэтому начало результирующего вектора будет скользить по положительной ветви спирали Корню, приближаясь к F+. Амплитуда результирующего колебания при этом монотонно стремится к нулю. То же можно сказать об изменении интенсивности в области геометрической тени.
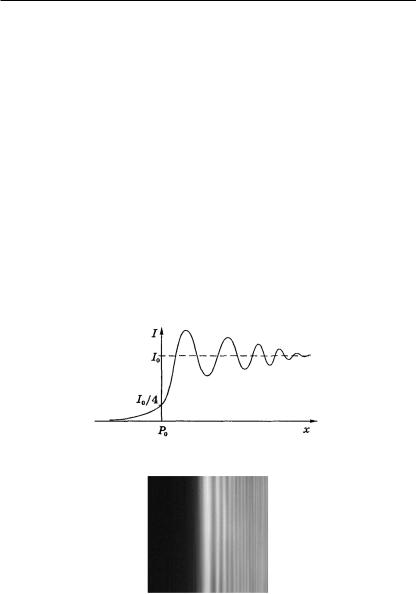
При смещении точки наблюдения от границы геометрической тени в области света (точка Р2) в дополнение к положительным зонам открывается все большее число отрицательных зон. Поэтому начало результирующего вектора скользит по отрицательной ветви спирали Корню, приближаясь к FÐ. Амплитуда колебания при этом осциллирует, становясь то больше Е0 (например, отрезки А1F+, А3F+ на рис. 4.14), то меньше Е0 (отрезки А2F+, А4F+ на рис. 4.14). Так же изменяется интенсивность света. В целом, зависимость интенсивности света от расстояния х, отсчитываемого от центральной точки Р на экране М, можно представить графиком, изображенным на рис. 4.16.
Дифракционная картина (рис. 4.17), очевидно, будет иметь вид чередующихся темных и светлых полос, параллельных краю дифракционного экрана N. На дифракционной картине отсутствует резкая граница светотени. Интенсивность света в области геометрической тени медленно спадает до нуля.
!"#. ).#,. F'/"#".-#%8 "*%)*#"/*-#%" #/)%' -% &'##%-G*"G
!"#. ).#-. A"4 4"?&'73"-**-< 7'&%"*=
4.3. Дифракция Фраунгофера |
187 |
Аналогично с помощью спирали Корню можно рассмотреть распределение интенсивности при дифракции света на других дифракционных препятствиях (щели, проволоке).
4.3. M/B.)*E/< @.)9#+$B'.)
Тип дифракции, при котором рассматривается дифракционная картина, образованная параллельными лучами, получил название дифракции Фраунгофера. Этот случай имеет большое практическое значение для решения многих вопросов инструментальной оптики.
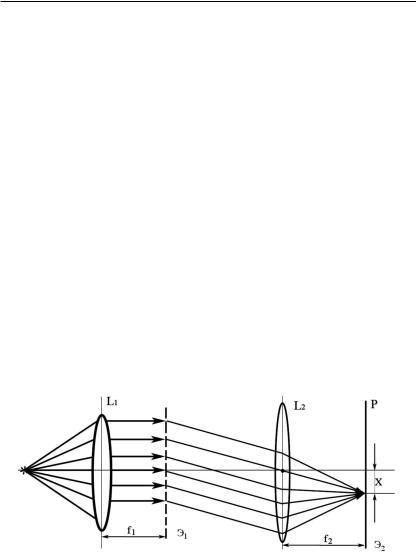
Дифракция Фраунгофера наблюдается в том случае, когда на препятствие, вызывающее дифракцию, попадает плоская волна, и точка наблюдения удалена от препятствия на расстояние L >> Lд, где Lд Ð длина дифракции. При этом параметр дифракции m << 1.
Чтобы наблюдать дифракцию Фраунгофера на конечных расстояниях, применяют классическую схему (рис. 4.18): точечный источник света помещают в фокусе собирающей линзы L1, таким образом получая плоскую волну, падающую на препятствие Э1; за препятствием помещают вторую собирательную линзу L2 и дифракционную картину исследуют в ее фокальной плоскости на экране Э2. Такую же дифракционную картину мы получили бы без линзы L2, если бы удалили экран Э2 на расстояние L >> Lд.
!"#. ).#/. Q,'##"2)#7'G #5).' 4,G *':,94)*"G
4"?&'73"" I&'1*0-?)&'
188 |
Тема 4. Дифракция света |
|
|
4.3.1. Дифракция на круглом отверстии
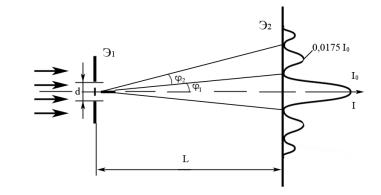
Случай дифракции на круглом отверстии очень важен практически, так как оправы линз и диафрагмы объективов в оптических приборах имеют обычно круглую форму. Расчет дифракционной картины на круглом отверстии представляет довольно большие трудности (при выполнении расчета задача приводится к бесселевым функциям). Заметим лишь, что дифракционная картина симметрична относительно оси отверстия и в центре всегда наблюдается максимум (рис. 4.19).
!"#. ).#1. ["?&'73"G I&'1*0-?)&' *' 7&10,-. -%/)%""
Приведем значение угловых радиусов колец и их интенсивности без вывода; d Ð диаметр отверстия (см. табл. 1).
Минимум |
Максимум |
Интенсивность |
||
sin φ1 |
= 1.22 λ/d |
sin φ 1 |
= 0 |
I0 |
sin φ2 |
= 2.23 λ/d |
sin φ 2 |
= 1.62 λ/d |
0.0175 Io |
sin φ3 |
= 3.24 λ/d |
sin φ 3 |
= 2.66 λ/d |
0.0042 Io |
sin φ4 |
= 4.24 λ/d |
sin φ4 |
= 3.70 λ/d |
0.0016 Io |
Заметим, что, зная угловой радиус кольца, легко найти его линейный радиус: Ri = L tg φi или в приближении малых углов Ri = L sin φi Для радиусов трех первых темных колец получим:
F" % "# |
ΑC |
%!F# % ". |
ΑC |
%!F. % .D |
ΑC |
&! |
(4.8) |
, |
, |
, |
4.3. Дифракция Фраунгофера |
189 |
|
|
4.3.2. Дифракция на одной щели
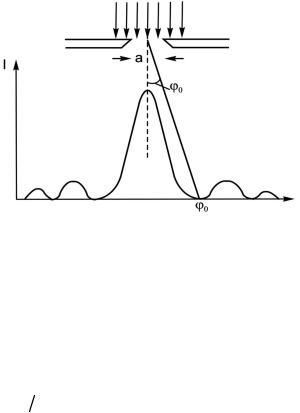
Согласно принципу Гюйгенса каждая точка плоскости щели размером a, до которой дошло световое возмущение, становится источником вторичных волн, распространяющихся во все стороны под различными углами дифракции. Дифракционные пучки когерентны и могут интерферировать при наложении. Результат интерференции в виде периодического распределения интенсивности наблюдается на экране (рис. 4.20).
!"#. ).$2. !'#+&)4),)*") "*%)*#"/*-#%" +&" 4"?&'73"" *' H),"
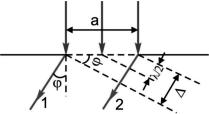
Воспользуемся методом зон Френеля для расчета углового положения максимумов и минимумов на экране. Если отверстием в экране является длинная щель, то зоны Френеля представляют собой полоски, вытянутые вдоль щели. Число зон N, умещающихся в щели, зависит от ее ширины a, длины волны λ, угла падения ) волны на щель
иугла дифракции φ. Если волна падает на щель нормально () = 0)
ирасстояние до экрана достаточно велико (L >> λ), то щель вмещает в себя число зон:
N ! a sin φ . |
(4.9) |
|||
|
! |
2 |
|
|
|
|
|||
Отрезок , = a ! sin φ является разностью хода волн, идущих от крайних элементов щели под углом φ к первоначальному направле-
нию (рис. 4.21).
190 |
Тема 4. Дифракция света |
|
|
!"#. ).$#. !'6*-#%8 5-4' /-,* +&" 4"?&'73"" *' H),"
Если в направлении φ открыто четное число зон, то = 2m(λ/2) и амплитуда результирующей волны Em(φ) = 0, т. е. в этих направлениях наблюдается минимумы интерференции. Максимумы наблюдаются
внаправлениях, для которых щель открывает нечетное число зон: = (2m+1) (λ/2).
Таким образом, метод зон Френеля приводит к следующим условиям:
для минимумов
а ! sin φ min = m λ, (4.10) где m = 1, 2, 3 и т. д.;
для максимумов
а ! sin φ max = (2m + 1) λ /2 , (4.11) где m = 0, 1, 2, 3 и т. д.
В соотношении (4.10) m не может быть нулем. Это соответствует простому физическому факту: точно за щелью всегда находится максимум интенсивности. С математической точки зрения это соответствует тому, что при = 0 выражение (4.9) обладает особенностью: для любой ширины в щели помещается всегда одна зона Френеля (причем нулевая). Часто число m называют порядком дифракционного минимума.
Следует иметь в виду, что формулы (4.9) Ð (4.11) носят приближенный характер и выполняются лишь при следующих предположениях о способе наблюдения дифракции:
1)свет падает на щель нормально;
2)угол дифракции не очень велик;
3)за щелью стоит собирающая линза (например, глаз) или экран находится достаточно далеко (L >> λ);
4)источник достаточно удален (L0 >> λ) или он находится в фокусе собирающей линзы (оба варианта соответствуют тому, что на щель падает плоская волна).
