Основы механики твердого деформируемого тела

к равенству F0 = 0, а тогда, согласно формуле (1.7a), обращалась бы в нуль и площадь любого поперечного сечения бруса. Этот результат естественен: при P = 0 и F (x) = 0 нет ни нагрузок на брус, ни самого бруса.

1.3. Гибкие нити. Среди строительных конструкций особое место занимают так называемые висячие конструкции: вантовые покрытия, подвесные мосты, линии электропередач. Элементами таких конструкций являются тросы, испытывающие только осевую деформацию. Изгибу, сдвигу и кручению длинный тонкий трос сопротивляться не может. Это обстоятельство подчеркивается и названием расчетной модели троса – гибкая нить.

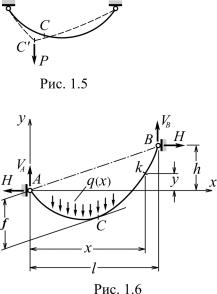
Смена нагрузки на нить может привести к резкому изменению ее положения равновесия. Сказанное иллюстрирует рис. 1.5, на котором сплошной линией показаны равновесная форма гибкой нити под действием собственного веса, а штриховой линией – положение равновесия той же нити после приложения дополнительной силы P . Большие перемещения точек нити, связанные с ее переходом в новое положение, могут проходить и без деформирования материала, т. е. без изменения длины нити, либо сопровождаться пренебрежимо малыми деформациями. В та-

ком случае говорят, что нить является нерастяжимой. К одной из основных задач, реша-

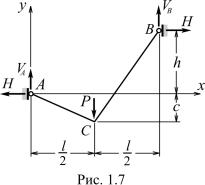
емых при исследовании напряженно-де- формированного состояния нитей, относится задача определения по заданному силовому воздействию равновесной формы нити при условии ее нерастяжимости. Здесь будут рассматриваться только плоские конструкции. В этом случае точки подвеса нити и нагрузка расположены в одной плоскости. Кроме того, предполагается, что нагрузка направлена вертикально вниз. Расстояние по горизонтали

между точками подвеса нити (рис. 1.6) называют пролетом и обозначают через l. Размер f , равный расстоянию между прямой AB и параллельной ей касательной к нити, принято называть стрелой провисания, или просто стрелой. Пролет l и расстояние h между точками подвеса нити по вертикали обычно задаются. Кроме того, для однозначного описания формы нити нужно указать либо ее полную длину L, либо стрелу. Из условия равновесияPx = 0 нити видно, что горизонтальные составляющие опорных реакций одинаковы. Эти составляющие обозначаются через H и называются распором. Для произвольной точки нити

где M0(x) – изгибающий момент, порождаемый только вертикальной нагрузкой – как заданной, так и реакцией VA. Точно такой же изгибающий момент возник бы в сечении k простой балки пролета l при воздействии q(x). Это позволяет называть величину M0(x) балочным изгибающим моментом. Так как нить изгибу не сопротивляется, то M (x) = 0 и из формулы (1.9) следует

Стало быть, находящаяся в положении равновесия гибкая нить имеет форму балочной эпюры изгибающих моментов, построенной от той же нагрузки, что приложена к нити.

Уравнение (1.10) можно преобразовать к виду, не содержащему величины M0(x). Для этого достаточно опереться на дифференциальные зависимости (I.1.9) между усилиями и интенсивностью распределенной нагрузки, полученные в п. I.1.8:

Двукратное дифференцирование уравнения (1.10) с учетом формул (1.11) дает:

Распор H остается пока неопределенным.

1.4. Равновесные формы некоторых нерастяжимых нитей. Если нить загружена сосредоточенными силами, то в промежутках между точками приложения сил уравнение (1.12) является однородным. Из этого следует, что нить имеет форму ломаной с участками

yi = aix + bi , i = 1, 2, . . . , m + 1, (1.13)

где m – число прикладываемых сил. Поло-

жения вершин ломаной определяются 2(m + 1) параметрами ai и bi. Последние связаны двумя граничными условиями и 2m условиями сопряжения прямых (1.13). Итак, на 2(m + 1) искомых параметров оси нити наложено столько же ограничений. Тем не менее этих условий для решения задачи недостаточно, ибо неизвестен распор H. Надо задать либо стрелу f провиса нити, либо ее полную длину L. Можно, конечно, ограничить и сам распор.

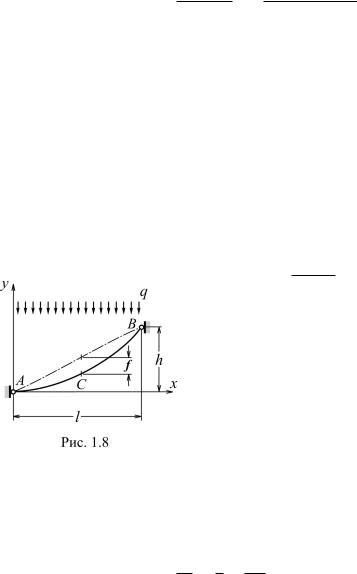
Пусть, например, к нити приложена заданная сосредоточенная сила P (рис. 1.7). Кроме значения силы и абсциссы точки ее приложения задаются также размеры l, h и L. Очевидно,

L = c2 + l2/4 + (h + c)2 + l2/4.

Эта зависимость однозначно определяет размер c, т. е. форму нити. Из условий равновесия нити в целом и равенства нулю изгибающего момента в любой точке ломаной ABC (например, в точке C) находят вертикальные составляющие опорных реакций и распор:

Задача решена.

Следующий пример относится к нити, несущей равномерно распределенную нагрузку. В частности, равномерно распределенной можно считать нагрузку от собственного веса пологой нити. Так называют нить, параметры которой удовлетворяют условию (рис. 1.8)

f / l2 + h2 < 0, 1 ÷ 0, 15.

При q =const уравнение (1.12) имеет решение y = qx2/2H + ax + b.

Постоянные a и b должны удовлетворять граничным условиям y(0) = 0 и y(l) = h, что дает

т. е. равновесное очертание оси нити под действием равномерно распределенной нагрузки имеет форму квадратной параболы.

Пусть задана стрела f провиса нити. Так как тангенс угла наклона касательной к нити в точке C равен отношению h/l, а (см. формулу (1.14))

dxdy = hl − 2qH (l − 2x),

то из равенства dy/dx = h/l следует xC = l/2. В таком случае yC = h/2 − f и координаты точки C найдены. Подстановка их в формулу (1.14) позволяет вычислить распор:

H = ql2/8f.

Если нить не является пологой, то нагрузку от ее собственного веса уже нельзя считать равномерно распределенной по координате x. Теперь к каждому элементу нити длиною ds прикладывается воздействие ρds, где ρ – вес единицы длины нити. Поскольку ρds = [1 + (y )2]1/2dx, то интенсивность q(x) рассматриваемой нагрузки равна величине ρ[1 + (y )2]1/2. При такой интенсивности уравнение (1.12) становится нелинейным:

где arcsh(p) – обратный гиперболический синус. Гиперболические синус и косинус –

sh(p) = (ep − e−p)/2, ch(p) = (ep + e−p)/2

при дифференцировании и интегрировании переходят друг в друга без сме-

Распор H пока неизвестен. Его можно задать. В случаях, когда величина H должна быть ограничена, так и поступают. Тогда второе из равенств (1.17) однозначно определяет постоянную a, а значит, и форму нити. Кроме того, для нахождения распора можно назначить длину нити либо стрелу. Пусть, например, концы нити подвешены на одном уровне (h = 0) и указан размер f . В этом случае соотношение (1.17)2 примет вид:

ch(ρl/H + a) = ch(a).

Гиперболический косинус – функция четная, так что a = −ρl/2H и

Остается учесть, что y(l/2) = −f :

f= (H/ρ) · [ch(ρl/2H) − 1],

азатем найти отсюда значение распора. Линия, описываемая равенством (1.16), называется цепной.

1.5.Натяжение нити. При известных форме нити и

распоре вычисление осевой силы N труда не составляет. По рис. 1.9 видно, что N = H/ cos α, а так как

cos α = 1/ 1 + tg2α, tgα = y ,

то

N = H 1 + (y )2. (1.18)

В точке, где y = 0, усилие N равно распору. В этом месте оно минимально. Наибольшего же значения натяжение нити достигает на одном из своих концов.

1.6. Пологая и непологая нити. Полученные в п. 1.3–1.5 результаты могут быть отнесены и к случаю растяжимой нити, но лишь при том условии, что нить неполога. Понять сказанное поможет следующий пример.

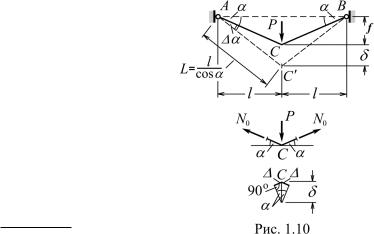
На рис. 1.10 сплошной линией показано равновесное положение нити, отвечающее силе P , до ее (нити) деформирования. В такой нити действует усилие

Ему по закону Гука соответствует удлинение ∆ каждого из участков конструкции:

Пусть отношение P/F близко к допускаемым напряжениям [σ] для материала, из которого изготовлен трос. Если трос стальной, то [σ]/E ≈ 10−3. Тогда

Для непологой нити перемещение δ пренебрежимо мало по сравнению с размером l. Например, при α = 30o

т. е. разница между усилиями (1.19) и (1.19a) настолько мала, что расчет можно вести по недеформированной схеме конструкции. Ситуация радикально меняется, если угол α мал. В этом случае

α≈ sin α ≈ tgα = f /l

и(см. формулы (1.19), (1.19a) и (1.20a)):

N0 = P l/2f, N = P l/2(f + δ), δ = 10−3l3/2f 2.

Пусть l/f = 10. Тогда

δ = 0, 05l, N0 = 5P, N = 3, 33P.

Таким образом, неучет растяжимости нити приводит к заметному завышению усилий.

Полученная оценка груба – ведь с уменьшением усилия N уменьшается и перемещение δ, а это обстоятельство было оставлено без внимания. Однако суть дела с ее помощью проясняется. Становится очевидным, что расчет пологих нитей нужно вести только по деформированной схеме конструкции. Для этого необходимо иметь полную систему уравнений, соответствующую геометрически нелинейной задаче.

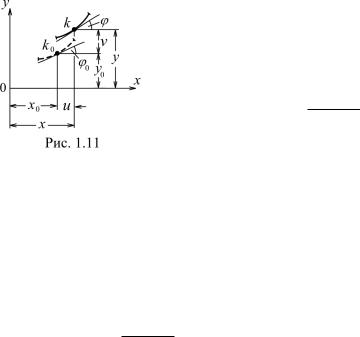
1.7. Полная система уравнений для плоской пологой нити. На приводимом ниже рис. 1.11 штриховой линией изображено положение равновесия, которое принял бы при заданной нагрузке некоторый участок пологой нити, будь таковая нерастяжимой. Если же осевая деформация учитывается, то равновесная форма того же участка нити будет иной (см. сплошную линию на рис. 1.11). В процессе деформирования точка k0 с координатами x0, y0 перейдет в положение k(x, y), причем

где u, v – компоненты вектора перемещения точки k0. Задача состоит в записи статических, кинематических и физических уравнений для произвольной точки нити.

Уравнение равновесия уже имеется – это соотношение (1.12), в котором под H понимается распор в деформированном состоянии нити:

Кинематическое уравнение предстоит вывести. Речь идет об условии совместности деформации ε и перемещений u и v. По определению,

ε = ds − ds0 , ds0

где ds0, ds – длины элемента нити до деформирования и после него. Так как (см. формулы (1.21))

ds20 = dx20 + dy02, ds2 = dx2 + dy2 = (dx0 + du)2 + (dy0 + dv)2,

то

ds2 − ds20 = (2dx0 + du)du + (2dy0 + dv)dv.

С другой стороны,

Здесь учтено, что отношение ds/ds0 близко к единице. Сопоставление двух выражений для разности квадратов величин ds и ds0 дает

Подчеркнутый член можно отбросить: он имеет порядок деформации, а потому пренебрежимо мал по сравнению с единицей. Таким образом,

Кинематическое уравнение задачи получено. Оно нелинейно, но здесь важно то, что форма нити представлена функцией y0(x0), отвечающей ее (нити) недеформированному состоянию. Линию же y0(x0), в отличие от кривой y(x), можно установить более или менее просто (см. п.1.3, 1.4).

Остается связать деформацию ε с усилием N . Пусть материал подчиняется закону Гука, т. е.

ε = σ/E = N/EF.

Пологие нити весьма чувствительны к изменению температуры, так что следует учесть и температурную деформацию

εt = αLT /L = αT.

В этой формуле α – коэффициент теплового расширения материала, L – длина нити, T – изменение температуры окружающей среды. Стало быть, полное относительное удлинение нити равно величине (см. также формулу (1.18)):

Сюда входит производная от искомой функции y(x), описывающей новую форму нити. Как отмечалось при обсуждении равенства (1.23), это неудобно. С другой стороны, даже при довольно больших перемещениях точек нити разница между углами наклона касательных к линиям y0(x0) и y(x) невелика. В таких случаях говорят, что деформирование конструкции характеризуется большими линейными перемещениями точек оси, но малыми поворотами поперечных сечений, и принимают ϕ ≈ ϕ0 (см. рис. 1.11). Если же y = y0, то связь между деформацией ε, температурой T и распором H принимает вид:

Физическое уравнение (1.24) вместе с равенствами (1.22) и (1.23) образует полную систему уравнений пологой гибкой нити. Из-за нелинейности зависимостей (1.23) и (1.24) эту систему в общем случае можно решить только численно.

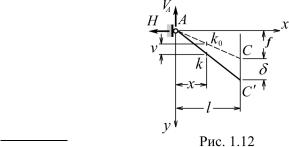
Конструкция, рассмотренная в предыдущем пункте (см. рис. 1.10), столь проста, что найти усилия и перемещения в ней удается без какихлибо осложнений и при нелинейной постановке задачи. Так как звенья AC и CB ломаной ACB остаются прямолинейными и после деформирования, то не только точка C, но и все остальные точки нити перемещаются лишь по вертикали, причем (рис. 1.12)

Это кубическое относительно безразмерного перемещения узла C уравнение можно решить численно. После того, как параметр η будет найден, по формулам (1.26) и (1.18) вычисляются распор и усилие N . При µ = 0, 1 и P/EF = 10−3 задача имеет решение:

η = 1/30, H = 15P/4, n = 3, 77P.

Результаты, полученные в п. 1.6, были иными: η = 1/20, N = 3, 33P . Следовательно, имелись все основания для квалификации их в названном пункте как весьма грубых.