Практическая работа № 11 «Расчеты на прочность при изгибе»
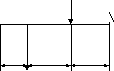
Цель:Построить эпюры поперечных сил и изгибающих моментов для балки, нагруженной сосредоточенными силами F1 и F2 и парой сил с моментом М; выполнить проектный расчет на прочность: подобрать сечение балки в двух вариантах указанных в таблице. Принять допускаемое напряжение: четный вариант [σ] = 160 МПа; нечетный вариант [σ] = 180 МПа;
Данные для своего варианта взять в таблице.
Таблица
|
Вариант |
Схема |
М |
F1 |
F2 |
Профиль |
Форма | ||
|
кН · м |
кН | |||||||
|
1 |
1 |
2 |
3 |
4 |
Двутавр |
Квадрат а · а | ||
|
2 |
2 |
5 |
6 |
7 |
Швеллер |
Прямоуг. h = 2b | ||
|
3 |
3 |
8 |
9 |
10 |
Двутавр |
Круг с ø d | ||
|
4 |
4 |
3 |
4 |
5 |
Швеллер |
Квадрат а · а | ||
|
5 |
5 |
6 |
7 |
8 |
Двутавр |
Прямоуг. h = 3b | ||
|
6 |
6 |
9 |
10 |
2 |
Швеллер |
Круг с ø d | ||
|
7 |
7 |
4 |
5 |
6 |
Двутавр |
Квадрат а · а | ||
|
8 |
8 |
7 |
8 |
9 |
Швеллер |
Прямоуг. h = 4b | ||
|
9 |
9 |
10 |
2 |
3 |
Двутавр |
Круг с ø d | ||
|
10 |
10 |
5 |
6 |
7 |
Швеллер |
Квадрат а · а | ||
|
11 |
11 |
8 |
9 |
10 |
Двутавр |
Прямоуг. h = 1,5b | ||
|
12 |
12 |
6 |
7 |
8 |
Швеллер |
Круг с ø d | ||
|
13 |
13 |
9 |
10 |
2 |
Двутавр |
Квадрат а · а | ||
|
14 |
14 |
3 |
4 |
6 |
Швеллер |
Прямоуг. h = 2b | ||
|
15 |
15 |
7 |
5 |
2 |
Двутавр |
Круг с ø d | ||
|
16 |
16 |
10 |
9 |
8 |
Швеллер |
Прямоуг. h = 3b | ||
|
17 |
17 |
5 |
4 |
3 |
Двутавр |
Круг с ø d | ||
|
18 |
3 |
2 |
1 |
10 |
Двутавр |
Квадрат а · а | ||
|
19 |
11 |
9 |
8 |
7 |
Швеллер |
Прямоуг. h = 2b | ||
|
20 |
15 |
6 |
5 |
4 |
Двутавр |
Круг с ø d | ||
|
21 |
7 |
3 |
2 |
1 |
Швеллер |
Квадрат а · а | ||
|
22 |
1 |
10 |
9 |
8 |
Двутавр |
Прямоуг. h = 3b | ||
|
23 |
13 |
7 |
6 |
5 |
Швеллер |
Круг с ø d | ||
|
24 |
6 |
4 |
3 |
2 |
Двутавр |
Квадрат а · а | ||
|
25 |
2 |
1 |
10 |
9 |
Швеллер |
Прямоуг. h = 4b | ||
|
26 |
14 |
8 |
7 |
6 |
Двутавр |
Круг с ø d | ||
|
27 |
10 |
5 |
4 |
3 |
Швеллер |
Квадрат а · а | ||
|
28 |
4 |
2 |
1 |
8 |
Двутавр |
Прямоуг. h = 1,5b | ||
|
29 |
8 |
3 |
2 |
5 |
Швеллер |
Круг с ø d | ||
|
30 |
16 |
5 |
6 |
7 |
Двутавр |
Квадрат а · а | ||
|
31 |
5 |
4 |
4 |
2 |
Швеллер |
Прямоуг. h = 2b | ||
|
32 |
9 |
3 |
9 |
8 |
Двутавр |
Круг с ø d | ||
|
33 |
12 |
2 |
7 |
5 |
Швеллер |
Прямоуг. h = 3b | ||
|
34 |
17 |
6 |
10 |
3 |
Двутавр |
Круг с ø d | ||
|
1 F1 M F2
2 м 4 м 3 м
|
2 F1 M
F2
3 м 4 м 2 м
|
3 F2 M
F1
2 м 5 м 3 м
|
|
4
F1 M
F2
3 м 4 м 6 м |
5 F1 M
F2 3 м 6 м 2 м
|
6
M F1
F2
2 м 6 м 4 м
|
|
7 F1 M F2
2 м 5 м 4 м
|
8 F2 F1 M
3 м 6 м 4 м
|
9 F1 M F2
2 м 5 м 3 м |
|
10 F2 F1 M
4 м 6 м 5 м
|
11
F1 F2 M
2 м 5 м 3 м
|
12 F2 F1 M
2 м 4 м 3 м
|
|
13 F1 F2 M
3 м 4 м 2 м
|
14 F1 M
F2
3 м 5 м 2 м
|
15
M F1
F2
3 м 4 м 3 м
|
|
16 F2 F1 M
2 м 3 м 2 м |
17 F1 M
F2 2 м 4 м 4 м |
|
