
2.3.1. Розрахунок верхнього днища
Рисунок 2 – Розрахунок верхнього днища

Геометрична форма верхнього днища – конус.
Для розрахунку його товщини з умов міцності скористаємось формулами, наведеними в [5]
p= pнад
+ nx*ρ*H*(1
+ )
)
В розрізі 1 – 1:
p= 0.585*106+ 0 = 0.585*106 (Па)
Для нижньої частини конуса розрахуємо тиск:
p
=0.585*106
+ 1*1400*1.089*(1 +
 )
= 6.135*105 (Па)
)
= 6.135*105 (Па)
Знайдемо внутрішні зусилля, що діють на конічне верхнє днище:
Nα
=
 +
+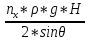 *r*[1
+ (
*r*[1
+ ( -
-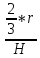 )*tg
)*tg ]
]
Nβ
=
 +
+ *r*[1
+ (
*r*[1
+ ( -
- )*tg
)*tg ]
]
Nα=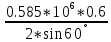 +
+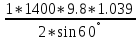 *0.6*[1
+ (
*0.6*[1
+ ( -
- )*tg60°]
= 2.142*105(Н/м)
)*tg60°]
= 2.142*105(Н/м)
Nβ= +
+ *0.6
*[1 + (
*0.6
*[1 + ( -
- )*tg
)*tg ]
= 4.251*105
(Н/м)
]
= 4.251*105
(Н/м)
Знайдемо потрібну мінімальну товщину верхнього днища з умов міцності:

 (днище стискається)
(днище стискається)

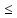
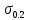
h

h - для верхньої частини
- для верхньої частини
h 5.874*10-3 (м)
5.874*10-3 (м)
Приймаємо товщину 5.9 мм з умов міцності .
Розрахуємо необхідну товщину верхнього днища з умов стійкості:
pкр
= kc*ρ*Et* *
*
ρ
= 3 – 2.3* ;R = 1.2 м;
R0 =
0.6 м
;R = 1.2 м;
R0 =
0.6 м
ρ
= 3 – 2.3* = 1.85
= 1.85
Et = 5.95*104 (МПа)
L = 1.2062 (м)
kc = 0.8
h


h


h
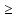 0.01115 (м)
0.01115 (м)
Отже, необхідна товщина верхнього днища з урахуванням умов міцності та стійкості h = 11.15 мм.
Перевіримо отримані результати:

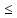



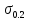
 138*106
138*106
Знайдемо коефіцієнти запасу міцності конічного днища:
ηміц
=
 =
=

Перевіримо розрахунки на стійкість:
pкр
=kc*ρ*Et* *
*
pкр
=0.8*1.85*5.95*1010* (cos30
(cos30 = 5.876*105(Па)
= 5.876*105(Па)
ηст
=
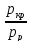
ηст=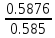 = 1.00444
= 1.00444
ηст ≥ 1, умова стійкості виконується
Проте, порівнюючи отримані коефіцієнти запасів, можна зробити висновок, що використання гладкого днища недоцільне, необхідно розрахувати вафельне днище.
.3.2. Розрахунок нижнього днища
Геометрична форма нижнього днища – сегмент сфери.
Розрахунки на міцність будемо вестиза [5]
Рисунок 3 – Розрахунок нижнього днища

Тиск на поверхні днища:
pn
= p = p0
+nx* *[H
+ R*(cos
*[H
+ R*(cos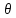 - cos
- cos
 0]
0]
Приймаємо радіус сферичного днища 1.2 м *1.3 = 1.56 м
Внутрішні зусилля:
Nα
=
 + nx*ρ*g*H*
+ nx*ρ*g*H* *[1
+
*[1
+ *(
*( -
-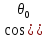 ]
]
 = 1.2/1.56, отже
= 1.2/1.56, отже
 0
= 50.28°
0
= 50.28°
Nβ
=
 nx*ρ*g*H*
nx*ρ*g*H* *[1
+
*[1
+ *(2*cos
*(2*cos - cos
- cos -
- )]
)]
Максимальні значення для внутрішніх зусиль:
Nα
max = Nβ
max
=
 nx*ρ*g*H*
nx*ρ*g*H* *[1
+
*[1
+ *(1
-
*(1
- ]
]
Nα
max = Nβ
max
=
 1*1400*9.8*7.92*
1*1400*9.8*7.92* *[1
+
*[1
+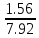 *(1
-
*(1
- ]
= = 0.46556 (МН/м)
]
= = 0.46556 (МН/м)
В місці спряження днища з кільцем маємо:
Nα
=
 nx*ρ*g*H*
nx*ρ*g*H* *[1
+
*[1
+ *(
*( -
- ]
]
Nα= *1400*9.8*7.92*
*1400*9.8*7.92* *[1
+
*[1
+ *(
*( -
- ]
==0.46528 (МН/м)
]
==0.46528 (МН/м)
Nβ= Nα*cos
Nβ= 0.46528* = 0.2973 (МН/м)
= 0.2973 (МН/м)
pn
= p = p0
+ nx*ρ*g*[H
+ R*(cos - cos
- cos
pA
= 0.585*106 +
1*1400*9.8*[7.92 + 1.56*( -
- )]
= 0.6936624 (МПа)
)]
= 0.6936624 (МПа)
pc
= 0.585*106 +
1*1400*9.8*[7.92 + 1.56*( -
- )]
= 0.701388177 (МПа)
)]
= 0.701388177 (МПа)
pk
= 0.585*106 +
1*1400*9.8*[7.92 + 1.56*( -
- )]
= 0.69638078 (МПа)
)]
= 0.69638078 (МПа)
pz
= 0.585*106 +
1*1400*9.8*[7.92 + 1.56*( -
-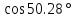 )]
= 0.6985207 (МПа)
)]
= 0.6985207 (МПа)
pc = pmax
Скористаємося третью теорією міцності для визначення необхідної товщини днища:
h =
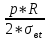
h =
 = 0.001824 (м). Приймаємо товщинуh
= 1.85 мм
= 0.001824 (м). Приймаємо товщинуh
= 1.85 мм
Виконаємо перевірку:
 =
=

 =
= = 1.016
= 1.016
Отже, умова міцності виконується.
2.4.1. Розрахунок верхнього шпангоута
Зробимо проектувальний розрахунок верхнього шпангоута, що працює на розтягнення, тобто визначимо його приведену площу. [2]
Nα
=
 =
=
Nβ
= Nα*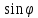 =
=
Nα= = 7.02*105 (Н/м)
= 7.02*105 (Н/м)
Nβ= *
* =
3.51*105(Н/м)
=
3.51*105(Н/м)
σшп
=

|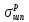 |
| σв t
σв t
Fпр


Fпр


Fпр
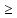 1.685*10-3
(м2)
1.685*10-3
(м2)
