8.4 Критерий согласия Пирсона

Критерием согласия называется критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Пусть по выборке объема п получено эмпирическое распределение:

Варианты xi	x1	x2	...	xs
Частоты ni	n1	n2	...	ns

С помощью критерия Пирсона можно проверить гипотезу о различных законах распределения генеральной совокупности (равномерном, нормальном, показательном и др.) Для этого в предположении о конкретном виде распределения вычисляются теоретические частоты , и в качестве критерия выбирается случайная величина

,

имеющая закон распределения χ² с числом степеней свободы k = s – 1 – r, где s – число частичных интервалов выборки, r – число параметров предполагаемого распределения. Критическая область выбирается правосторонней, и граница ее при заданном уровне значимости α находится по таблице критических точек распределения χ².

Теоретические частоты вычисляются для заданного закона распределения как количества элементов выборки, которые должны были попасть в каждый интервал, если бы случайная величина имела выбранный закон распределения, параметры которого совпадают с их точечными оценками по выборке, а именно:

а) для проверки гипотезы о нормальном законе распределения =п∙ Р_i, где п – объем выборки, x_i и x_{i + 1} – левая и правая границы i-го интервала, - выборочное среднее,s – исправленное среднее квадратическое отклонение. Поскольку нормальное распределение характеризуется двумя параметрами, число степеней свободы k = n – 3;

б) для проверки гипотезы о показательном распределении генеральной совокупности в качестве оценки параметра λ принимается . Тогда теоретические частоты=п∙ Р_i, . Показательное распределение определяется одним параметром, поэтому число степеней свободыk = n– 2;

в) для проверки гипотезы о равномерном распределении генеральной совокупности концы интервала, в котором наблюдались возможные

значения Х, оцениваются по формулам:

Тогда плотность вероятности

Число степеней свободы k = n– 3, так как равномерное распределение оценивается двумя параметрами.

9. Практическая часть

9.1 Часть I

№25(Задача 1)

Построить ряд распределения числа попаданий мячом в корзину при четырех бросках, если вероятность попадания равна 0,7.

P₀=0,3⁴=0,081;

P₁=*P*q³=*0,7*0,3³=4*0,7*0,027=0,0756;

P₂=*P²*q²=*0,7²*0,3²=6*0,09*0,49=0,2646;

P₃=*P³*q=*0,7³*0,3=4*0,343*0,3=0,4116;

P₄=*P⁴=0,7⁴=0,2401;

Xi	0	1	2	3	4
Pi	0,081	0,0756	0,2646	0,4116	0,2401

№ 62 (Задача2) Случайные величины X и Y заданы законами распределений. Определить: 1) математическое ожидание 2) дисперсию 3) среднее квадратическое отклонение величин X и Y 4) составить законы распределения случайных величин Z=X+Y, V=XY 5) построить многоугольник распределения случайной величины Z 6) математическое ожидание и дисперсию случайной величины W=2X-4Y

X	-10	-6	-1
p	0,4	P2	0,2

Y	-1	2
q	0,2	0,8

так как 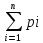=1, тоp₂=1-(0.4+0.2)=0.4

Решение: 1) M(x)=-10*0,4-6*0,4*-1*0,2=-6,6; М(y)=-1*0,2+2*0,8=1,4 М(x²)=100*0,4+36*0,4+1*0,2=54,6 M(y²)=1*0,2+2*0,8=3,4 2) D(x)=M(x²)-M²(x)=54,6-(-6,6²)=54,6-43,56=11,04 D(y)=M(y²)-M²(y)=3,4-(1,4)²=0,61 3) ==3,32==1,2

4) Z=X+Y – Закон распределения для Z

Zi	-11	-8	-7	-4	-2	1
Pi	0,08	0,32	0,08	0,32	0,04	0,16

V=X*Y

Vi	10	-20	6	-12	1	-2
Pi	0,08	0,32	0,08	0,32	0,04	0,16

5) многоугольник распределения случайной величины Z

Wi	-16	-28	-8	-20	2	-6
Pi	0,08	0,32	0,08	0,32	0,04	0,16

6) W=2X-4Y

M(W)=(-16*0,08)+(-28*0,32)+(-8*0,08)+(-20*0,32)+(2*0,04)+(-6*0,16)=-18,16 M(W²)=(-16²*0,08)+ (-28²*0,32)+(-8²*0,08)+(-20²*0,32)+(2²*0,04)+(-6²*0,16)=410,4

D(W)=M(W²)-M²(W)=410,4-(-18,16²)=410,4-329,7856=80,6144;

Вариант №16 ЗАДАНИЕ 2.1. По имеющимся данным построить закон распределения заданной случайной величины (см. варианты задания). Необходимо:

1. Построить вариационный (или интервальный) ряд исследуемой случайной величины.

2. Произвести группировку данных вариационного ряда на 6 - 10 интервалов (разрядов, групп), построить таблицу частот, вычислить и представить графически эмпирические функции распределения исследуемой случайной величины.

3. Определить основные характеристики выборочной совокупности для исследуемой случайной величины.

4. Построить доверительные интервалы для среднего и дисперсии заданной случайной величины (выбрать α = 0,05; 0,01; 0,1 самостоятельно).

Вариант 16: Месячный процент премии на предприятии (%): 15, 16, 18, 20, 20, 25, 27, 28, 22, 18, 16, 15, 15, 16, 18, 21, 23, 25, 25, 22, 18, 16, 20, 19, 18, 16, 21,23,26,28,30,32

Максимальное	32	Границы интервалов	Абсолютные частоты	Относительные частоты	Накопленные частоты
Минимальное	15,00	16,89	8	0,25	0,25
		18,78	5	0,15625	0,40625
		20,67	4	0,125	0,53125
		22,56	4	0,125	0,65625
		24,44	2	0,0625	0,71875
		26,33	4	0,125	0,84375
		28,22	3	0,09375	0,9375
		30,11	1	0,03125	0,96875
		32,00	1	0,03125	1
			32

x среднее	21,00
мода	16
медиана	20
диспесия	22,70968
Сред.квад.откл	4,765467
Ассиметрия	0,597099
эксцес	-0,56819

Построение доверительного интервала

Для среднего
Х средн.выборочное	21
выборочн.ск.	4,765467177
Доверит.вер.	0,95
Уровень значимости	0,05
N	33
t(alpha;n-1)	46,19425944
delta	38,32097249
Граница 1	-17,32097249
Граница 2	59,32097249

Для дисперсии
Х средн.выборочное	21
Дисперсия	22,70968
Доверит.вероятн.	0,9
Alpha	0,1
n	33
XИ(alpha/2;n-1)	42,58475
ХИ(1-alpha/2;n-1)	22,27059
Граница 1	17,06503
Граница 2	32,63091