Задача легко решается для идеально-газовой смеси, поскольку для нее

и так как то

и, следовательно, состав равновесной системы зависит от знака Σ ν_i , т.е. от знака изменения числа молей газообразных участников реакции. Однако, как мы увидим ниже, случай, когда Σ ν_i = 0, требует дополнительного изучения.

15.8. Расчет константы равновесия по таблицам термодинамических величин.

Из вышеизложенного очевидно, что для определения направления химического процесса в системе данного состава необходимо знать величину константы равновесия при данной температуре.

Тепловой эффект химической реакции и ее энтропия () при 298,15 К легко рассчитываются с помощью энтальпий образования () и абсолютных энтропий () участников химической реакции по закону Гесса :

При температурах, отличающихся от условной (298 К)

таким образом необходимо знать зависимость теплоемкостей участников химического процесса от температуры и тогда при температуре T > 298 K

и

Практически стоит иметь в виду, что два интеграла в правой части приблизительно равны по величине и противоположны по знаку, поэтому для оценочных расчетов можно записать

Точный расчет можно выполнить следующим образом (метод Темкина – Шварцмана, 1948). При температурах выше 298 К зависимость теплоемкости вещества от температуры аппроксимируется полиномом :

следовательно тоже полином:

Далее по уравнению Гиббса-Гельмгольца

Разделим переменные и возьмем интегралы от 298 до Т

Так как Δ а, Δ b, Δ d и Δ m от температуры не зависят, то интегралы берутся без труда и

Выражения, стоящие при Δ а, Δ b, Δ d и Δ m являются функциями только температуры, обозначаются М₀ , М₁ , М₂ и М_-2 могут быть заранее вычислены и табулированы, что сделали Темкин и Шварцман. Значения этих коэффициентов приводятся в справочниках физико-химических величин. Таким образом :

Пример. Рассчитать константу равновесия и степень диссоциации водяного пара при 2000 К.

	-241840	0	0	Дж/моль
	188,74	130,6
а	30,00	27,28
в
т

При 2000 К

Тогда

Степень диссоциации рассчитаем следующим образом. Если был взят 1 моль водяного пара, то после диссоциации α молей Н₂О образовалось при равновесии α молей Н₂ и молейО₂ . Общее число молей газовой смеси станет

тогда мольные доли реагентов равны :

Если общее давление Р , то парциальные давления :

и следовательно

Таким образом, имея величину К_р и задав давление Р, можно вычислить α. Выражение можно упростить, если тогда

и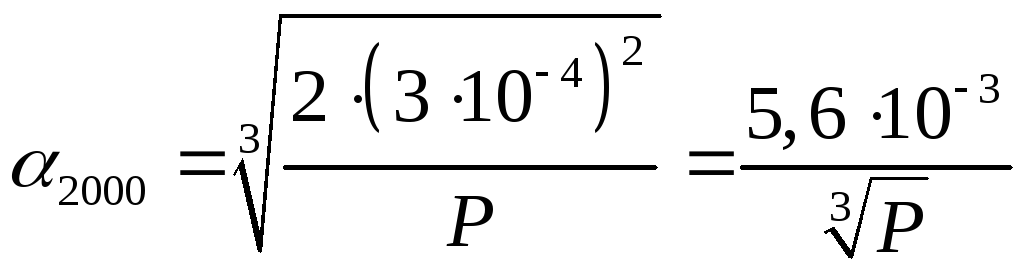

Если Р = 1 атм , то

15.9. Расчет константы равновесия в неидеальных газовых системах.

В газообразной системе, где давление достаточно велико, условие равновесия приводит к выводу, что

где f_i - летучесть i –ого компонента. Поскольку где γ_i - коэфициент летучести, то очевидно, что

Поскольку при р = 1 атм, коэфициенты летучести равны единице, то численное значение K_f очевидно равно величине K_p при р = 1.

Для расчета величин γ удобно воспользоваться законом соответственных состояний.

Пример. Реакция и давление как будто не должно влиять на состав равновесной системы. Рассмотрим эту систему при 900К и500 атм

	Ркр	Ткр	τ	π	γ
СО	34,6	134	6,72	14,45	1,2
Н2О	218,5	647	1,39	2,29	0,7
Н2	12,8	33	21,9	24,05	1,1
СО2	73	304	2,96	6,84	1,1

Отсюда

Следовательно, состав равновесной смеси сдвигается в сторону исходных веществ при увеличении давления.

Пример. Равновесие синтеза аммиака.

1 моль исходной стехиометрической смеси, а при равновесии получаем х молей аммиака.

Температура 723 К

Ратм	хэксп
1	0,0021	6,50	1	1	1	6,50
10	0,0204	6,59	1,003	1,005	0,997	6,53
30	0,0380	6,76	1,01	1,014	0,991	6,55
50	0,0917	6,90	1,015	1,024	0,985	6,57
100	0,1636	7,25	1,03	1,047	0,970	6,57
300	0,355	8,84	1,09	1,14	0,910	6,62
600	0,536	12,94	1,18	1,33	0,83	7,27
1000	0,694	23,28	1,36	1,61	0,89	10,39

Примечание : коэфициенты летучести найдены исходя из закона соответственных состояний, как .

Например, при 300 атм К_γ = 0,795

Подставив величины иР , получаем расчетное что очень близко к экспериментальной величине 0,355.Из таблицы видно также, что при давлениях выше 300атм постоянства K_f не наблюдается, но это, очевидно, связано со способом оценки величин γ по закону соответственных состояний.