7.2. Реализация сложных логических функций на интегральных микросхемах.

Учитывая ограниченный ассортимент интегральных микросхем по числу выполняемых операций для практической реализации произвольных логических функций часто необходимо представить их через единственную операцию «И-НЕ» или»ИЛИ-НЕ». Такое преобразование выполняется в три этапа.

1) Составление функционального уравнения (ФАЛ).

На этом этапе выписывают комбинации переменных для которых искомая функция – «истина» т.е. равна 1. Каждая комбинация записывается в виде произведения переменных и все полученные произведения суммируют.

Пример: рассмотрим логическую схему, применяемую для выделения сигнала из помех, а также для определения переноса в следующий разряд при поразрядном сложении чисел в двоичной системе. На вход поступают три логических сигнала. На выходе напряжение равно единице только в том случае, когда, по крайней мере, два сигнала равны 1. Данное условие можно записать

.

Для отыскания всех возможных комбинаций переменных, обеспечивающих единичное значение функции, используют таблицы состояний.

2) Преобразование функционального уравнения с целью упрощения.

а) Использование алгебры логики.

.

Тогда

(7.1).

б) Построение диаграмм Вейча или карт Карно.

3) Дальнейшее преобразование уравнения с целью приведения его к виду, реализуемому заданными интегральными схемами.

Пусть имеем только элементы «И-НЕ». Тогда уравнение (7.1) сводиться к виду согласно теореме де-Моргана

.

Последнее выражение можно представить схемой на рис.7.7.

Рис.7.7.

7.3. Упрощение логических выражений с помощью диаграмм Карно-Вейча.

Карта Карно или диаграмма Вейча это определённая форма таблицы истинности. На рис 7.8. представлены карты двух, трёх и четырёх переменных. Расположение групп переменных x_i не имеет значения, необходимо лишь, чтобы каждая ячейка отличалась от любой соседней лишь на одну переменную. Согласно принятой форме построения карт соседними ячейками также считаются ячейки первой и последней строк, ячейки первого и последнего столбцов. Число ячеек карты равно числу возможных комбинаций значений логических переменных и в каждую ячейку записывается значение логической функции, соответствующее данному набору переменных.

Рис.7.8.

Алгоритм минимизации логического выражения заключается в следующем.

1. На карте выделяют прямоугольные области со смежными ячейками равными 1. Каждая область должна содержать 2^k ячеек, где k – целое число. Одну и туже ячейку можно использовать более одного раза. Угловые ячейки также можно объединять в область. Можно объединять не ячейки с 1, а ячейки с нулями и взять инверсную функцию.

2. Из полученного множества выбирают минимальное число максимально больших областей и суммируют их логические функции.

Для представления функции пяти аргументов необходимо использовать две карты для четырёх переменных: одна для х₅=1 и вторая – х₅=0. Эти карты располагаются одна под другой и области охвата клеток могут быть трёхмерными, т.е. в одну область могут входить клетки двух карт.

Для функции шести аргументов используют четыре пары карт четырёх переменных с заданными .

Для большего числа переменных карты не используются, а применяют алгебраические методы ( метод Квайна и Мак-Класки, метод неопределённых коэффициентов и др.).

Примеры.

1. Карта для двух переменных.

Пусть . Карта имеет вид

Логическая функция соответствующая выделенной области , и .

2. Карта трёх переменных.

Пусть карта построенная по таблице истинности имеет вид. Выделяем две области.

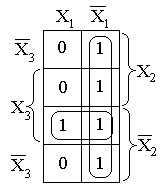
Полученное выражение равно .

3. Карта четырёх переменных.

Внутренняя квадратная область соответствует выражению . Четыре угловых ячейки можно объединить, свернув таблицу в виде тора, и соответствующее области выражение есть . Общее выражение тогда получиться .