Задания по теме: "Векторы"
.docЗадача № 1
Вычислить
площадь параллелограмма, построенного
на векторах
и
(таблица
1). Найти длину вектора
.
Таблица№ 1
|
№ варианта |
|
|
|
|
|
|
1 |
|
|
1 |
2 |
|
|
2 |
|
|
4 |
1 |
|
|
3 |
|
|
1/5 |
1 |
|
|
4 |
|
|
4 |
1/2 |
|
|
5 |
|
|
2 |
3 |
|
|
6 |
|
|
2 |
3 |
|
|
7 |
|
|
3 |
2 |
|
|
8 |
|
|
7 |
2 |
|
|
9 |
|
|
1 |
2 |
|
|
10 |
|
|
7 |
3 |
|
|
11 |
|
|
10 |
1 |
|
|
12 |
|
|
5 |
4 |
|
|
13 |
|
|
6 |
7 |
|
|
14 |
|
|
3 |
4 |
|
|
15 |
|
|
2 |
3 |
|
|
16 |
|
|
4 |
1 |
|
|
17 |
|
|
1 |
2 |
|
|
18 |
|
|
1/2 |
2 |
|
|
19 |
|
|
3 |
4 |
|
|
20 |
|
|
4 |
1 |
|
|
21 |
|
|
8 |
1/2 |
|
|
22 |
|
|
5/2 |
2 |
|
|
23 |
|
|
3 |
1 |
|
|
24 |
|
|
3 |
5 |
|
|
25 |
|
|
7 |
2 |
|
|
26 |
|
|
5 |
3 |
|
|
27 |
|
|
2 |
3 |
|
|
28 |
|
|
1/2 |
4 |
|
|
29 |
|
|
2 |
1 |
|
|
30 |
|
|
2 |
3 |
|
Образец решения задачи № 1
Пусть
,
,
значения модулей
,
,
а угол между векторами
=
.
Определим
площадь параллелограмма построенного
на векторах
и
:
.
Найдём
длину вектора
:
.
Задача № 2
Даны координаты вершин пирамиды АВСD (таблица 2). Найти объём пирамиды, площадь грани АВС и угол между ребрами АВ и АО.
Таблица № 2
|
№ варианта |
А |
В |
С |
D |
|
1 |
(1,3,6) |
(2,2,1) |
(-1,0,1) |
(-4,6,-3) |
|
2 |
(-4,2,6) |
(2,-3,0) |
(-10,5,8) |
(-5,2,-4) |
|
3 |
(7,2,4) |
(7,-1,-2) |
(3,3,1) |
(-4,2,1) |
|
4 |
(2,1,4) |
(-1,5,-2) |
(-7,-3,2) |
(-6,-3,6) |
|
5 |
(-1,-5,2) |
(-6,0,-3) |
(3,6,-3) |
(-10,6,7) |
|
6 |
(0,-1,-1) |
(-2,3,5) |
(1,-5,-9) |
(-1,-6,3) |
|
7 |
(5,2,0) |
(2,5,0) |
(1,2,4) |
(-1,1,1) |
|
8 |
(2,-1,-2) |
(1,2,1) |
(5,0,-6) |
(-10,9,-7) |
|
9 |
(-2,0,-4) |
(-1,7,1) |
(4,-8,-4) |
(1,-4,6) |
|
10 |
(14,4,5) |
(-5,-3,2) |
(-2,-6,-3) |
(-2,2,-1) |
|
11 |
(1,2,0) |
(3,0,-3) |
(5,2,6) |
(8,4,-9) |
|
12 |
(2,-1,2) |
(1,2,-1) |
(3,2,1) |
(-4,2,5) |
|
13 |
(1,1,2) |
(-1,1,3) |
(2,-2,4) |
(-1,0,-2) |
|
14 |
(2,3,1) |
(4,1,-2) |
(6,3,7) |
(7,5,-3) |
|
15 |
(1,1,-1) |
(2,3,1) |
(3,2,1) |
(5,9,-8) |
|
16 |
(1,5,-7) |
(-3,6,3) |
(-2,7,3) |
(-4,8,-12) |
|
17 |
(-3,4,-7) |
(1,5,-4) |
(-5,-2,0) |
(2,5,4) |
|
18 |
(-1,2,-3) |
(4,-1,0) |
(2,1,-2) |
(3,5,4) |
|
19 |
(4,-1,3) |
(-2,1,0) |
(0,-5,1) |
(3,2,-6) |
|
20 |
(1,-1,1) |
(-2,0,3) |
(2,1,-1) |
(2,-2,-4) |
|
21 |
(1,2,0) |
(1,-1,2) |
(0,1,-1) |
(4,4,-2) |
|
22 |
(1,0,2) |
(1,2,-1) |
(2,-2,1) |
(-3,0,1) |
|
23 |
(1,2,-3) |
(1,0,1) |
(-2,-1,6) |
(2,1,0) |
|
24 |
(3,10,-1) |
(-2,3,-5) |
(-6,0,-3) |
(1,-1,2) |
|
25 |
(-1,2,4) |
(-1,-2,-4) |
(3,0,-1) |
(7,-3,1) |
|
26 |
(0,-3,1) |
(-4,1,2) |
(2,-1,5) |
(3,1,-4) |
|
27 |
(1,3,0) |
(4,-1,2) |
(3,0,1) |
(-4,3,5) |
|
28 |
(-2,-1,-1) |
(0,3,2) |
(3,1,-4) |
(-4,7,3) |
|
29 |
(-3,-5,6) |
(2,1,-4) |
(0,-3,-1) |
(-5,2,-8) |
|
30 |
(2,-4,-3) |
(5,-6,0) |
(-1,3,-3) |
(-10,-8,7) |
Образец решения задачи № 2
Пусть координаты вершин А, В, С и D равны:
А(1,-1,2); В(2,1,2); С(1,1,4); D(6,-3,8).
Введём в рассмотрение следующие векторы:
,
,
.
Объём пирамиды вычисляем по формуле
.
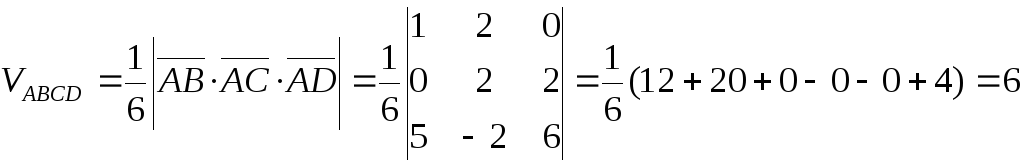Далее
определим векторное произведение
векторов
и
:
.
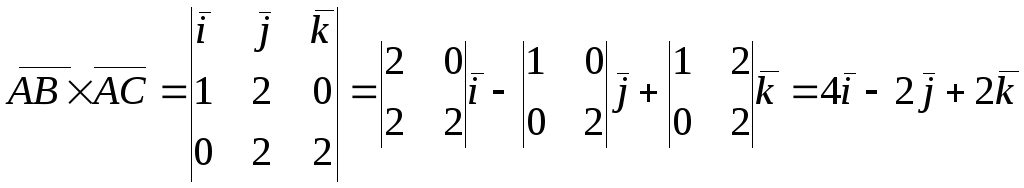Тогда площадь грани АВС определяем по формуле:
.
Найдём угол между рёбрами АВ и АD
,
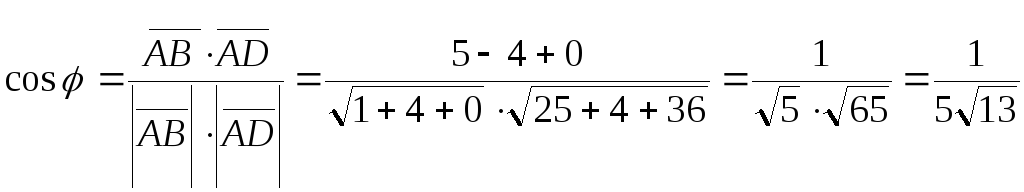то
есть
.
Задача № 3
Заданы
векторы
,
,
и
своими координатами в некотором базисе
(таблица 3). Показать, что векторы
,
,
образуют базис. Найти координаты вектора
в базисе
,
,
.
Таблица № 3
|
№ варианта |
|
|
|
|
|
1 |
(0,1,2) |
(1,0,1) |
(-1,2,4) |
(-2,4,7) |
|
2 |
(1,3,0) |
(2,-1,1) |
(0,-1,2) |
(6,12,-1) |
|
3 |
(2,1,-1) |
(0,3,2) |
(1,-1,1) |
(1,-4,4) |
|
4 |
(4,1,1) |
(2,0,-3) |
(-1,2,1) |
(-9,5,5) |
|
5 |
(-2,0,1) |
(1,3,-1) |
(0,4,1) |
(-5,-5,5) |
|
6 |
(5,1,0) |
(2,-1,3) |
(1,0,-1) |
(13,2,7) |
|
7 |
(0,1,1) |
(-2,0,1) |
(3,1,0) |
(-19,-1,7) |
|
8 |
(1,0,2) |
(0,1,1) |
(2,-1,4) |
(3,-3,4) |
|
9 |
(3,1,0) |
(-1,2,1) |
(-1,0,2) |
(3,3,-1) |
|
10 |
(-1,2,1) |
(2,0,3) |
(1,1,-1) |
(-1,7,-4) |
|
11 |
(1,1,4) |
(0,-3,2) |
(2,1,-1) |
(6,5,-14) |
|
12 |
(1,-2,0) |
(-1,1,3) |
(1,0,4) |
(6,-1,7) |
|
13 |
(1,0,5) |
(-1,3,2) |
(0,-1,1) |
(5,15,0) |
|
14 |
(1,1,0) |
(0,1,-2) |
(1,0,3) |
(2,-1,11) |
|
15 |
(1,0,2) |
(-1,0,1) |
(2,5,-3) |
(11,5,-3) |
|
16 |
(2,0,1) |
(1,1,0) |
(4,1,2) |
(8,0,5) |
|
17 |
(0,1,3) |
(1,2,-1) |
(2,0,-1) |
(3,1,8) |
|
18 |
(1,2,-1) |
(3,0,2) |
(-1,1,1) |
(8,1,12) |
|
19 |
(1,4,1) |
(-3,2,0) |
(1,-1,2) |
(-9,-8,-3) |
|
20 |
(0,1,-2) |
(3,-1,1) |
(4,1,0) |
(-5,9,-13) |
|
21 |
(0,5,1) |
(3,2,-1) |
(-1,1,0) |
(-15,5,6) |
|
22 |
(1,0,1) |
(0,-2,1) |
(1,3,0) |
(8,9,4) |
|
23 |
(2,1,0) |
(1,-1,0) |
(-3,2,5) |
(23,-14,-30) |
|
24 |
(2,1,0) |
(1,0,1) |
(4,2,1) |
(3,1,3) |
|
25 |
(0,3,1) |
(1,-1,2) |
(2,-1,0) |
(-1,7,0) |
|
26 |
(1,-1,2) |
(3,2,0) |
(-1,1,1) |
(11,-1,4) |
|
27 |
(1,1,4) |
(-3,0,2) |
(1,2,-1) |
(-13,2,18) |
|
28 |
(0,-2,1) |
(3,1,-1) |
(4,0,1) |
(0,-8,9) |
|
29 |
(0,1,5) |
(3,-1,2) |
(-1,0,1) |
(8,-7,-13) |
|
30 |
(1,0,1) |
(1,-2,0) |
(0,3,1) |
(2,7,5) |
