
Funktsionalny_analiz
.docx(Т1)
Аддитивный оператор y=Ax,
определённый на линейном вещественном
пространстве Lx,
непрерывный в одной точке x0∈Lx,
непрерывен на всё Lx.
(ДОКАЗАТЕЛЬСТВО) Пусть х – произвольная
точка из Lx.
Пусть последовательность {xn}
сходится к х, т.е. xn→x.
Тогда xn-x+x0→x0.
Т.к. оператор А непрерывен в точке x0,
то
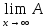 (xn-x+x0)=Ах0.
Т.к. А аддитивен, то А(xn-x+x0)=
Аxn-Аx+Аx0,
то А(х0)=
(xn-x+x0)=Ах0.
Т.к. А аддитивен, то А(xn-x+x0)=
Аxn-Аx+Аx0,
то А(х0)=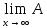 (xn-x+x0)=
(xn-x+x0)=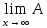 xn-Аx+Аx0
=
xn-Аx+Аx0
=
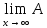 хn
- Аx+Аx0;
хn
- Аx+Аx0;
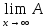 хn=Ах.
(ДОК)
хn=Ах.
(ДОК)
В
множестве линейных непрерывных операторов
можно ввести алгебраические операции.
Сложение операторов А и В определяется
по формуле: (А+В)х = Ах + Вх. Умножение на
число: (αА)х = α(Ах). Т.о. множество линейных
операторов является линейным пространством.
Нулём этого пространства является
нулевой оператор. В линейном пространстве
операторов определяется предел
последовательности операторов {An},
полагая, что An→A,
если
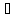 х∈Lx
будет
х∈Lx
будет
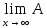 хn=Ах.
Определим произведение операторов А и
В формулой: (АВ)х = А(Вх). Видим, что это
тоже линейный оператор, непрерывный на
Lx.
По индукции определяется произведение
любого числа операторов. Пишут АА=А2,
ААА=А2А=А3,
… . Кроме того, (АВ)С=А(ВС); (А+В)С=АС+ВС;
С(А+В)=СА+СВ. Существует единичный оператор
Ix=x,
причём AI=IA=A.
Т.о.. множество линейных непрерывных
операторов образует кольцо с единицей;
кольцо не коммутативное, т.к. АВ
хn=Ах.
Определим произведение операторов А и
В формулой: (АВ)х = А(Вх). Видим, что это
тоже линейный оператор, непрерывный на
Lx.
По индукции определяется произведение
любого числа операторов. Пишут АА=А2,
ААА=А2А=А3,
… . Кроме того, (АВ)С=А(ВС); (А+В)С=АС+ВС;
С(А+В)=СА+СВ. Существует единичный оператор
Ix=x,
причём AI=IA=A.
Т.о.. множество линейных непрерывных
операторов образует кольцо с единицей;
кольцо не коммутативное, т.к. АВ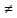 ВА.
ВА.
№24) Линейные операторы в линейный нормированных пространствах.
Пусть Lx и Ly – линейные нормированные пространства. Т.к. линейные нормированные пространства – частный случай линейных топологических пространств, то определение линейного оператора, заданного на Lx со значениями в Ly переносится без изменений из предыдущего параграфа.
Т.к. сходимость в Lx и в Ly есть сходимость по норме, то непрерывность оператора А означает, что ||Axn – Ax||→0, если ||xn – x||→0, где первая норма – норма пространства Ly, а вторая – норма пространства Lx.
(О)
Оператор А называется ограниченным,
если существует такая постоянная М >0,
что ||Ax||≤M||x||,
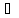 x∈Lx,
где ||x||
берётся в смысле метрики пространства
Lx,
а норма ||Ax||
- в смысле метрики пространства Ly.
Согласно этому определению ограниченный
оператор преобразует ограниченное
множество {x}
x∈Lx,
где ||x||
берётся в смысле метрики пространства
Lx,
а норма ||Ax||
- в смысле метрики пространства Ly.
Согласно этому определению ограниченный
оператор преобразует ограниченное
множество {x}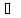 Lx
в ограниченное множество {Ax}
Lx
в ограниченное множество {Ax}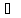 Ly.
Ly.
(Т1)
Аддитивный и однородный оператор А
непрерывен т т т, когда он ограничен.
(ДОКАЗАТЕЛЬСТВО) (необходимость) Пусть
оператор А является непрерывным.
Допустим, что он неограничен. Тогда
найдётся такая последовательность
{xn},
что ||Axn||>
n||xn||.
Построим элементы tn=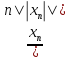 .
Тогда ||tn||=||
.
Тогда ||tn||=||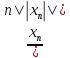 ||=
||=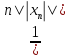 *||xn||=
*||xn||=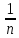 → 0. Т.о. tn
→ 0. Т.к. А непрерывен,
то должно быть Atn
→ 0. Однако считаем ||Atn||=||
→ 0. Т.о. tn
→ 0. Т.к. А непрерывен,
то должно быть Atn
→ 0. Однако считаем ||Atn||=||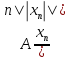 ||=
||=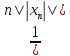 *||Axn||
>
*||Axn||
>
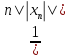 *
A||xn||
= 1. Откуда следует, что Atn
*
A||xn||
= 1. Откуда следует, что Atn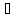 0. противоречие.
необходимость доказана. (достаточность)
Пусть А ограничен, т.е. ||Ax||≤M||x||.
Пусть xn→x,
т.е. ||xn-x||→0.
Тогда рассмотрим ||Axn-Ax||=||A(xn-x)||≤M||xn-x||→0.
Значит Axn→Ax,
т.е. оператор А непрерывен (ДОК).
0. противоречие.
необходимость доказана. (достаточность)
Пусть А ограничен, т.е. ||Ax||≤M||x||.
Пусть xn→x,
т.е. ||xn-x||→0.
Тогда рассмотрим ||Axn-Ax||=||A(xn-x)||≤M||xn-x||→0.
Значит Axn→Ax,
т.е. оператор А непрерывен (ДОК).
Пусть
А – линейный ограниченный оператор.
Наименьшее из постоянных чисел М,
удовлетворяющее условию ||Ax||≤M||x||
называется нормой оператора А и
обозначается через ||A||.
Итак, по определению число ||A||
обладает 2-мя свойствами: 1) ||Ax||≤||A||*||x||,
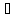 x∈Lx;
2)
x∈Lx;
2)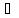 ε>0
найдётся элемент xε
такой, что ||Axε||>
(||A||-ε)||xε||.
ε>0
найдётся элемент xε
такой, что ||Axε||>
(||A||-ε)||xε||.
(Т2)
Для любого ограниченного оператора А,
действующего из нормированного
пространства в нормированное,
||A||=sup||x||≤1||Ax||=
supx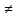 0
0
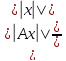 .
(ДОКАЗАТЕЛЬСТВО) равенство sup||x||≤1||Ax||=
supx
.
(ДОКАЗАТЕЛЬСТВО) равенство sup||x||≤1||Ax||=
supx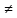 0
0
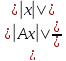 справедливо в силу однородности оператора
А. Значит осталось показать
||A||=sup||x||≤1||Ax||
(1). Пусть ||x||≤1.
Тогда ||Ax||≤||A||*||x||≤||A||.
Отсюда sup||x||≤1||Ax||≤||A||
(2). С другой стороны
справедливо в силу однородности оператора
А. Значит осталось показать
||A||=sup||x||≤1||Ax||
(1). Пусть ||x||≤1.
Тогда ||Ax||≤||A||*||x||≤||A||.
Отсюда sup||x||≤1||Ax||≤||A||
(2). С другой стороны
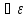 >0
существует элемент xε
такой, что ||Axε||>
(||A||-ε)||xε||.
Положим
>0
существует элемент xε
такой, что ||Axε||>
(||A||-ε)||xε||.
Положим
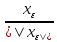 =tε.
Тогда ||Аtε||=||A
=tε.
Тогда ||Аtε||=||A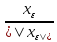 ||=
||=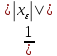 *||Axε||
>
*||Axε||
>
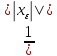 *
(A
- ε)*||xε||
= ||A||
- ε. Т.к. ||tε||=1,
то sup||x||≤1||Ax||≥||Аtε||>
||A||
- ε. Отсюда sup||x||≤1||Ax||≥||A||(3).
Из (2) и (3) следует (1). (ДОК)
*
(A
- ε)*||xε||
= ||A||
- ε. Т.к. ||tε||=1,
то sup||x||≤1||Ax||≥||Аtε||>
||A||
- ε. Отсюда sup||x||≤1||Ax||≥||A||(3).
Из (2) и (3) следует (1). (ДОК)
Пусть
в линейном нормированном пространстве
Lx
задано линейное многообразие L.
Это многообразие можно рассматривать
как самостоятельное линейное пространство.
Пусть на L
определён линейный оператор А со
значениями в линейном нормированном
пространстве Ly.
Оператор А называется ограниченным на
L,
если существует постоянная M>0
такая, что ||Ax||≤M||x||,
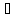 x∈L.
Наименьшая из таких постоянных М
называется нормой оператора А на L
и обозначается ||A||L.
В соответствии с этим норму на всём
пространстве Lx
иногда будем обозначать ||A||Lx.
x∈L.
Наименьшая из таких постоянных М
называется нормой оператора А на L
и обозначается ||A||L.
В соответствии с этим норму на всём
пространстве Lx
иногда будем обозначать ||A||Lx.
(Т3)
Линейный оператор А0,
заданный на линейном многообразии L,
всюду плотном, в линейном нормированном
пространстве Lx
со значениями в полном линейном
нормированном пространстве Ly,
может быть продолжен на всё Lx
без увеличения нормы. (ДОКАЗАТЕЛЬСТВО)
Пусть х∈Lх,
но х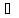 L.
Т.к. L
всюду плотно в Lx,
то найдётся последовательность {xn},
xn∈L,
сходящаяся к x.
Т.е. ||xn
– x||→0
при n→
L.
Т.к. L
всюду плотно в Lx,
то найдётся последовательность {xn},
xn∈L,
сходящаяся к x.
Т.е. ||xn
– x||→0
при n→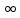 .
Т.к. хn
сходится, то она фундаментальна, т.е.
||xn-xm||→0
при n,m→
.
Т.к. хn
сходится, то она фундаментальна, т.е.
||xn-xm||→0
при n,m→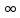 .
Тогда ||A0xn
– A0xm||=||A0(xn-xm)||≤||A0||L*||xn-xm||→0
при n,m→
.
Тогда ||A0xn
– A0xm||=||A0(xn-xm)||≤||A0||L*||xn-xm||→0
при n,m→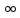 .
Значит последовательность {A0xn}
фундаментальна, а т.к. Ly
полно, то {A0xn}
сходится к некоторому пределу Ax∈Ly.
Возьмём последовательность {tn}
.
Значит последовательность {A0xn}
фундаментальна, а т.к. Ly
полно, то {A0xn}
сходится к некоторому пределу Ax∈Ly.
Возьмём последовательность {tn}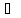 L,
сходящуюся тоже к х. Тогда ||xn
– tn||→0
при n→
L,
сходящуюся тоже к х. Тогда ||xn
– tn||→0
при n→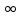 .
Откуда ||Atn-Axn||→0
при n→
.
Откуда ||Atn-Axn||→0
при n→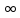 .
Значит At
сходится к Ах. Этим показано, что оператор
А определён на Lx
однозначно. Если х∈L,
то берём xn=x,
.
Значит At
сходится к Ах. Этим показано, что оператор
А определён на Lx
однозначно. Если х∈L,
то берём xn=x,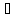 n
и тогда Ax=
n
и тогда Ax=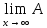 0xn=
0xn=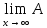 0x=A0x.
Оператор А аддитивен. Действительно
берём А(х1+х2)
=
0x=A0x.
Оператор А аддитивен. Действительно
берём А(х1+х2)
=
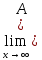 0x1n
+ A0x2n)
=
0x1n
+ A0x2n)
=
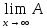 0x1n
+
0x1n
+
 0x2n
= Ах1
+ Ах2.
Оператор А ограничен. Действительно,
из неравенства ||A0xn||≤||A0||L
||xn||,
переходя к пределу,
получим ||Ax||≤||A0||L
||x||.
Отсюда ||A||Lx≤||A0||L.
Т.к. при продолжении оператора норма
уменьшится не может, то ||A||Lx≤||A0||L.
(ДОК)
0x2n
= Ах1
+ Ах2.
Оператор А ограничен. Действительно,
из неравенства ||A0xn||≤||A0||L
||xn||,
переходя к пределу,
получим ||Ax||≤||A0||L
||x||.
Отсюда ||A||Lx≤||A0||L.
Т.к. при продолжении оператора норма
уменьшится не может, то ||A||Lx≤||A0||L.
(ДОК)
Итак, на Lx можно определить оператор А такой, что Ах=А0х, х∈L и ||A||L=||A0||L. Этот процесс распространения оператора называется продолжением оператора по непрерывности.
№25) Пространство линейных ограниченных операторов.
Всевозможные
линейные операторы, определённые на
одном и том же линейном пространстве
Lx
со значениями в линейном пространстве
Ly
образуют линейное пространство (Lx→Ly).
Если Lx
и Ly
– нормированные пространства, то в
пространстве (Lx→Ly)
тоже можно ввести норму. Действительно,
для линейного ограниченного оператора
А, отображающего Lx
в Ly
норма определена в предыдущем параграфе.
Эта норма удовлетворяет всем аксиомам
нормы. Действительно, 1) ||A||=sup||x||≤1||Ax||≥0.
Если ||A||=0,
т.е.sup||x||≤1||Ax||=0.
Отсюда ||Ax||=0
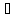 x,
||x||≤1.
В силу однородности ||Ax||=0.
x,
||x||≤1.
В силу однородности ||Ax||=0.
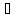 x.
Отсюда Ax=0,
x.
Отсюда Ax=0,
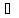 х.
Значит А=0. 2)||λA||=
sup||x||≤1||λAx||=|λ|
sup||x||≤1||Ax||=|λ|*||A||.
3) ||A1+A2||=
sup||x||≤1||A1x+A2x||
≤ sup||x||≤1||A1x||+
sup||x||≤1||A2x||
= ||A1||+||A2||.
Итак, пространство линейных ограниченных
операторов является линейным пространством.
х.
Значит А=0. 2)||λA||=
sup||x||≤1||λAx||=|λ|
sup||x||≤1||Ax||=|λ|*||A||.
3) ||A1+A2||=
sup||x||≤1||A1x+A2x||
≤ sup||x||≤1||A1x||+
sup||x||≤1||A2x||
= ||A1||+||A2||.
Итак, пространство линейных ограниченных
операторов является линейным пространством.
(Т1) Если Ly полно, то пространство линейных ограниченных операторов тоже является полным.
В частном случае, когда Ly=R, т.е. когда рассматриваем пространство линейных функционалов, то пространство (Lx→Ly) называется сопряжённым пространством с Lx и обозначается через Lx*.
(СЛЕДСТВИЕ) Пространство Lx* является полным пространством.
Сходимость последовательности {An} линейных ограниченных операторов в смысле сходимости по норме в пространстве этих операторов называют равномерной сходимостью. Часто используется ещё и другая сходимость. Последовательность {An} линейных ограниченных операторов называется точечно сходящейся или сходящейся в себе, если для каждого фиксированного х последовательность {Anx} сходится к Ах. Из равномерной сходимости следует точечная сходимость. Обратное не верно.
(Т2)
(Теорема Банаха – Штейнхауса) Если {An}
линейных непрерывных операторов
ограничена в каждой точке Банахового
пространства Х, т.е. {||Anx||}≤M,
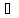 n,
то последовательность норм {||Anx||}
этих операторов тоже ограничена.
n,
то последовательность норм {||Anx||}
этих операторов тоже ограничена.
(СЛЕДСТВИЕ)
Если последовательность линейных
ограниченных операторов сходится в
себе в каждой точке Банахового пространства
Х, то последовательность норм этих
операторов ограничена. (ДОКАЗАТЕЛЬСТВО)
Последовательность таких операторов,
сходящихся в каждой точке Банахового
пространства, ограничена в каждой точке.
Утверждение следствия вытекает из
теоремы Банаха – Штейнхауса. Возвращаемся
к оператору Ах=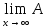 nx.
Из неравенства ||Anx||
≤ ||An||
||x||,
вытекающего из следствия в пределе
получаем ||Anx||≤M*||x||.
Значит А тоже ограничен. (ДОК)
nx.
Из неравенства ||Anx||
≤ ||An||
||x||,
вытекающего из следствия в пределе
получаем ||Anx||≤M*||x||.
Значит А тоже ограничен. (ДОК)
Т.о. предел любой точечно сходящейся последовательности линейных ограниченных операторов существует и является тоже линейным ограниченным оператором. Значит пространство операторов является полным и в смысле точечной сходимости.
№26) Обратные операторы.
Пусть оператор А действует их Х в Y. DA – область определения, EA – множество значений оператора.
(О1)
Оператор А называется обратимым, если
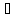 y∈EA
уравнение Ах=y,
имеет единственное решение.
y∈EA
уравнение Ах=y,
имеет единственное решение.
Если А обратим, то каждому y∈EA соответствует единственное x∈ DA. Оператор, осуществляющий это соответствие, называется обратным к А, обозначается через А—1, пишут х=А—1y.
(Т1) Оператор А—1, обратный к линейному оператору А, тоже линеен.(ДОКАЗАТЕЛЬСТВО) Пусть y1 и y2 ∈ ЕА, причём y1=Ax1, y2=Ax2. Тогда y1+y2=Ax1+Ax2=A(x1+x2). Значит x1+x2=A(y1+y2)= А—1y1 + А—1y2. Т.о. оператор А—1 аддитивен. Далее, если y∈EA и y=Ax, то λy=λAx=Aλx. Отсюда следует λx= А—1(λy)=λА—1y. Т.е. А—1 однороден. (ДОК)
(Т2)
Чтобы линейный оператор А имел ограниченный
обратный необходимо и достаточно, чтобы
существовало число m>0
такое, что ||Ax||
≥ m||x||,
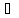 x∈DA.
(1). При этом max{m}=
x∈DA.
(1). При этом max{m}= .
(ДОКАЗАТЕЛЬСТВО) (необходимость) Пусть
условие (1) выполнено. Возьмём некоторый
y∈EA
и положим, x=
А—1y.
Подставим в (1). Получим ||y||≥m||
А—1y||.
Отсюда || А—1y||≤
.
(ДОКАЗАТЕЛЬСТВО) (необходимость) Пусть
условие (1) выполнено. Возьмём некоторый
y∈EA
и положим, x=
А—1y.
Подставим в (1). Получим ||y||≥m||
А—1y||.
Отсюда || А—1y||≤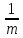 ||y||.
Отсюда || А—1||=
sup||y||≤1||
А—1y||
≤
||y||.
Отсюда || А—1||=
sup||y||≤1||
А—1y||
≤
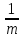 sup||y||≤1||y||
=
sup||y||≤1||y||
=
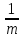 .
Т.о. А—1
ограниченный оператор и его норма ||
А—1||=
.
Т.о. А—1
ограниченный оператор и его норма ||
А—1||=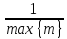 .
(достаточность) Пусть существует
ограниченный оператор А—1
и постоянная M>0
такая, что || А—1y||≤M||y||,
.
(достаточность) Пусть существует
ограниченный оператор А—1
и постоянная M>0
такая, что || А—1y||≤M||y||,
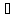 y∈EA.
Возьмём х∈DA.
Положим y=Ax.
Тогда x=
А—1y.
Значит ||x||≤M||Ax||.
Отсюда ||Ax||
≥
y∈EA.
Возьмём х∈DA.
Положим y=Ax.
Тогда x=
А—1y.
Значит ||x||≤M||Ax||.
Отсюда ||Ax||
≥
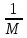 ||x||,
||x||,
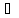 x∈
DA.
Сопоставив с (1), видим, что m=
x∈
DA.
Сопоставив с (1), видим, что m=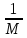 ,
т.е.
,
т.е.
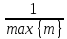 =min{M}=||
А—1||.
(ДОК)
=min{M}=||
А—1||.
(ДОК)
(Т3) Теорема Банаха об обратном операторе) Пусть А – линейный ограниченный оператор, отображающий взаимно однозначно Банахово пространство В1 на Банахово пространство В2. Тогда обратный оператор А—1 ограничен.
№27) Непрерывные линейные функционалы.
Если
значениями оператора являются вещественные
числа, то оператор называется функционалом.
Т.к. R
является Банаховым пространством, то
для линейных функционалов сохранятся
все определения и теоремы для линейных
операторов. Если линейный функционал
непрерывен в одной точке x∈Е,
то он непрерывен в Е всюду. Функционал
f,
определённый на Е, называется непрерывным,
если
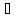 ε>0
и
ε>0
и
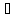 x0∈Е
существует окрестность U
точки x0
такая, что |f(x)-f(x0)|≤ε,
если x∈U.
Итак, проверять непрерывность линейного
функционала достаточно в одной точке,
например в точке 0. Если Е – нормированное
пространство, то непрерывность линейного
функционала можно сформулировать в
терминах последовательностей: если
xn→x,
то f(xn)→f(x).
x0∈Е
существует окрестность U
точки x0
такая, что |f(x)-f(x0)|≤ε,
если x∈U.
Итак, проверять непрерывность линейного
функционала достаточно в одной точке,
например в точке 0. Если Е – нормированное
пространство, то непрерывность линейного
функционала можно сформулировать в
терминах последовательностей: если
xn→x,
то f(xn)→f(x).
(Т1)
Чтобы линейный функционал был непрерывен
на Е необходимо и достаточно, чтобы в Е
существовала такая окрестность нуля,
на которой f
ограничен. (ДОКАЗАТЕЛЬСТВО) (необходимость)
Пусть линейный функционал f
непрерывен в точке х=0. Тогда
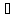 ε>0
существует такая окрестность U,
на которой |f(x)-f(0)|=f(x)<ε.
(достаточность) Пусть U
– такая окрестность нуля, что |f(x)|≤M,
ε>0
существует такая окрестность U,
на которой |f(x)-f(0)|=f(x)<ε.
(достаточность) Пусть U
– такая окрестность нуля, что |f(x)|≤M,
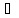 x∈U.
Возьмём
x∈U.
Возьмём
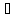 ε>0.
Тогда на окрестности нуля
ε>0.
Тогда на окрестности нуля
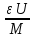 =U0.
Имеем |f(y)-f(0)|=f(
=U0.
Имеем |f(y)-f(0)|=f(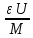 )=
)=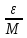 |f(x)|≤
|f(x)|≤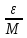 M=ε,
M=ε,
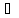 y∈U0.
Отсюда следует, что f
непрерывен в точке х=0. (ДОК).
y∈U0.
Отсюда следует, что f
непрерывен в точке х=0. (ДОК).
Линейный функционал, ограниченный на всяком ограниченном множестве, называется ограниченным линейным функционалом. Из ограниченности линейного функционала не следует, что он непрерывен.
