
Funktsionalny_analiz
.docx2)
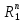 .
ρ(x,y)=
.
ρ(x,y)=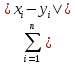 .
ρ(y1,y2)=
.
ρ(y1,y2)=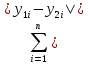 =
=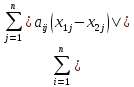 ≤
≤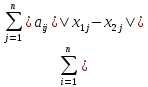 =
=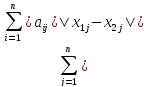 ≤
≤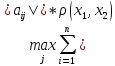 .
Т.о. отображение будет сжимающим, если
.
Т.о. отображение будет сжимающим, если
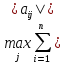 ≤α<1,
j=
≤α<1,
j=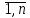 (3). Т.о. нужно взять сумму модулей всех
коэффициентов системы по столбцам
(матрицы). Наибольшая из этих сумм должна
быть < 1 (критерий по столбцам) .
(3). Т.о. нужно взять сумму модулей всех
коэффициентов системы по столбцам
(матрицы). Наибольшая из этих сумм должна
быть < 1 (критерий по столбцам) .
3)Rn.
ρ(x,y)=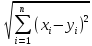 .
Используя неравенство Коши – Буняковского,
получим ρ2(y1,y2)=
.
Используя неравенство Коши – Буняковского,
получим ρ2(y1,y2)=
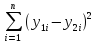 =
=
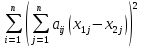 ≤
≤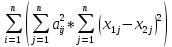 =
=
 *
ρ2(x1,x2).
По условию сжимаемости
*
ρ2(x1,x2).
По условию сжимаемости
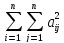 ≤α<1
(4).
≤α<1
(4).
Итак,
если выполнено хотя бы одно из условий
(2), (3), (4), то исходная система линейных
уравнений имеет единственное решение
x=(x1
, … , xn)
такое, что xi=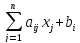 ,
i=
,
i= .
Это решение можно находить методом
последовательных приближений. В качестве
начальной точки x0
можно брать любую точку из Rn.
.
Это решение можно находить методом
последовательных приближений. В качестве
начальной точки x0
можно брать любую точку из Rn.
№8) Интегральные уравнения.
Рассмотрим
уравнение f(x)=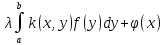 (1).
Это уравнение называется линейным
интегральным уравнением Фредгольма.
Здесь k(x,y)
и
(1).
Это уравнение называется линейным
интегральным уравнением Фредгольма.
Здесь k(x,y)
и
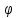 (x)
- заданные функции; f(x)
– искомая функция; λ – произвольный
параметр. Функция k(x,y)
называется ядром интегрального уравнения.
Пусть k(x,y)
и
(x)
- заданные функции; f(x)
– искомая функция; λ – произвольный
параметр. Функция k(x,y)
называется ядром интегрального уравнения.
Пусть k(x,y)
и
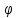 (x)
– непрерывные прямоугольники a≤x≤b,
a≤y≤b.
Т.к. k(x,y)
непрерывна в ограниченной замкнутой
области, то k(x,y)
ограничена, т.е. |k(x,y)|<M
при a≤x≤b,
a≤y≤b.
Рассмотрим отображение g=Af
полного метрического пространства
C[a,b]
в себя, задаваемое
формулой g(x)=
(x)
– непрерывные прямоугольники a≤x≤b,
a≤y≤b.
Т.к. k(x,y)
непрерывна в ограниченной замкнутой
области, то k(x,y)
ограничена, т.е. |k(x,y)|<M
при a≤x≤b,
a≤y≤b.
Рассмотрим отображение g=Af
полного метрического пространства
C[a,b]
в себя, задаваемое
формулой g(x)=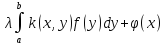 .
ρ(g1,g2)=
.
ρ(g1,g2)= =
=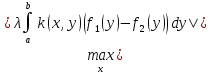 =|λ|M(b-a)
=|λ|M(b-a)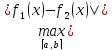 = |λ|M(b-a)
ρ(f1,f2).
Отображение А будем считать сжимающим,
если |λ|M(b-a)
< 1, т.е. если |λ|
<
= |λ|M(b-a)
ρ(f1,f2).
Отображение А будем считать сжимающим,
если |λ|M(b-a)
< 1, т.е. если |λ|
<
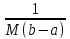 (2). Итак, по принципу сжимающих отображений
уравнение Фредгольма (1) имеет единственное
решение в пространстве C[a,b],
если выполнено условие (2). Последовательное
приближение f0,f1,…,fn
к этому решению имеет вид fn=
(2). Итак, по принципу сжимающих отображений
уравнение Фредгольма (1) имеет единственное
решение в пространстве C[a,b],
если выполнено условие (2). Последовательное
приближение f0,f1,…,fn
к этому решению имеет вид fn=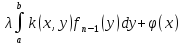 .
В качестве f0(x)
можно взять любую непрерывную на [a,b]
функцию. Принцип сжимающих отображений
можно применить и к нелинейным уравнениям
вида f(x)=
.
В качестве f0(x)
можно взять любую непрерывную на [a,b]
функцию. Принцип сжимающих отображений
можно применить и к нелинейным уравнениям
вида f(x)=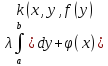 .
.
Рассмотрим
теперь интегральное уравнение вида
f(x)=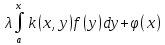 (3). Уравнение (3) называется линейным
уравнением Вальтерра. Здесь верхний
предел в интеграле является переменной
величиной х. Формально уравнение (3)
можно рассматривать как частный случай
уравнения Фредгольма, доопределив ядро
равенством k(x,y)=0
при y>x.
Однако, в случае интегрального уравнения
Фредгольма мы ограничиваемся только
малыми значениями параметра λ, а к
уравнению Вальтерра принцип сжимающего
отображения подходит при всех λ.
(3). Уравнение (3) называется линейным
уравнением Вальтерра. Здесь верхний
предел в интеграле является переменной
величиной х. Формально уравнение (3)
можно рассматривать как частный случай
уравнения Фредгольма, доопределив ядро
равенством k(x,y)=0
при y>x.
Однако, в случае интегрального уравнения
Фредгольма мы ограничиваемся только
малыми значениями параметра λ, а к
уравнению Вальтерра принцип сжимающего
отображения подходит при всех λ.
(Т1)
Если А – такое непрерывное отображение
полного метрического пространства Х в
себя, что Аn
при некотором n
является сжимающим, т.е. ρ(Аnx,
Аny)≤αρ(x,y),
α<1. Тогда уравнение Ax=x
имеет одно и только одно решение.
(ДОКАЗАТЕЛЬСТВО) Обозначим Аn=В,
т.е. В – сжимающее отображение. Тогда В
имеет единственную неподвижную точку
х, т.е. Вх=х. Имеем Ах=А*Вкх=Вкх0
→ х при к→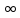 .
Т.к. отображение В сжимающее, поэтому
.
Т.к. отображение В сжимающее, поэтому
 х0
х0 Х
последовательность Вх0,В2х0,…,Вкх0,…
сходится к неподвижной точке отображения
В. Т.о. Ах=х и эта неподвижная точка
единственна, т.к. любая точка, неподвижная
относительно А, будет неподвижной и
относительно An,
а для В неподвижная точка х единственна.
(ДОК)
Х
последовательность Вх0,В2х0,…,Вкх0,…
сходится к неподвижной точке отображения
В. Т.о. Ах=х и эта неподвижная точка
единственна, т.к. любая точка, неподвижная
относительно А, будет неподвижной и
относительно An,
а для В неподвижная точка х единственна.
(ДОК)
Рассмотрим
теперь отображение А f(x)=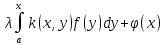 .
Покажем, что некоторая степень отображения
А является сжимающим отображением.
Пусть f1
и f2
– непрерывные функции на сегменте
[a,b],
т.е. принадлежат C[a,b].
|Af1(x)
– Af2(x)|=
.
Покажем, что некоторая степень отображения
А является сжимающим отображением.
Пусть f1
и f2
– непрерывные функции на сегменте
[a,b],
т.е. принадлежат C[a,b].
|Af1(x)
– Af2(x)|=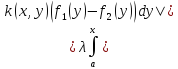 ≤|λ|M(x-a)
≤|λ|M(x-a)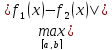 ,
где М=
,
где М=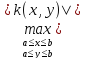 и т.д. |Anf1(x)
– Anf2(x)|≤
|λ|nMn
и т.д. |Anf1(x)
– Anf2(x)|≤
|λ|nMn
 .
ρ(Аnx,
Аny)≤
|λ|nMn
.
ρ(Аnx,
Аny)≤
|λ|nMn
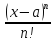 ρ(x1,x2)
При любом λn
число n
можно выбрать таким большим, что |λ|nMn
ρ(x1,x2)
При любом λn
число n
можно выбрать таким большим, что |λ|nMn
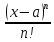 < 1. Действительно, рассмотрим ряд
< 1. Действительно, рассмотрим ряд
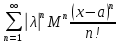 .
.
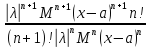 =
=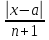 →0 при n→
→0 при n→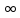 .
Если ряд сходится, то общий член стремится
к нулю при n→
.
Если ряд сходится, то общий член стремится
к нулю при n→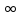 .
Т.о. отображение An
при некотором n
является компактным. Значит уравнение
Вальтерра имеет единственное решение
при любом λ.
.
Т.о. отображение An
при некотором n
является компактным. Значит уравнение
Вальтерра имеет единственное решение
при любом λ.
№9) Топологические пространства.
Основные понятия теории метрических пространств – предельная точка, точка прикосновения, замыкание множества, непрерывность и т.д. – вводятся, опираясь на понятие окрестности или, что в сущности одно и то же, на понятие открытого множества. Понятие окрестности определяется с помощью метрики, заданной в метрическом пространстве. Однако, можно идти другим путём, а именно, не определяя в данном множестве Х метрику, сразу указать в множестве Х открытое множество. Этот путь приводит к топологическим пространствам, по отношению к которым метрические пространства являются частным случаем.
(О1)
Пусть Х – некоторое множество. Топологией
в Х называется любая система τ его
подмножеств G,
удовлетворяющая аксиомам: 1)Само множество
Х и пустое множество принадлежат τ; 2)
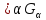 любого (конечного или бесконечного) и
любого (конечного или бесконечного) и
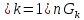 конечного числа множеств из τ принадлежат
τ. Множество Х с заданной в нём топологией
τ, т.е. пара (Х, τ) называется топологическим
пространством. Множества принадлежащие
системе τ называется открытыми
множествами.
конечного числа множеств из τ принадлежат
τ. Множество Х с заданной в нём топологией
τ, т.е. пара (Х, τ) называется топологическим
пространством. Множества принадлежащие
системе τ называется открытыми
множествами.
Итак, задать топологическое пространство – значит задать некоторое множество Х и указать те его подмножество, которые считаются открытыми.
Ясно, что в одном и том же множестве Х можно задать разные топологии, получая разные топологические пространства. Топологическое пространство, т.е. пару (Х , τ) часто будем обозначать одной буквой, например Т. Элементы множества Х будем называть точками. Множества Х\G дополнительные к открытым называются замкнутыми множествами.
Из
аксиомы 1) и 2) => 1)пустое множество и
всё Х замкнуты; 2)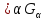 любого (конечного или бесконечного) и
любого (конечного или бесконечного) и
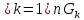 конечного числа замкнутых множеств
замкнуты. Эти утверждения следуют из
теории множеств.
конечного числа замкнутых множеств
замкнуты. Эти утверждения следуют из
теории множеств.
(О)
Окрестностью точки х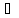 Т
называется всякое открытое множество
G
Т
называется всякое открытое множество
G Т,
содержащее х.
Т,
содержащее х.
(О)
Точка х Т
называется точкой прикосновения
множества М
Т
называется точкой прикосновения
множества М Т,
если каждая окрестность точки х содержит
хотя бы одну точку из М.
Т,
если каждая окрестность точки х содержит
хотя бы одну точку из М.
(О) Точка х называется предельной точкой множества М, если каждая окрестность точки х содержит бесконечно много точек из М.
(О) Совокупность всех точек прикосновения множества М называется замыканием множества М и обозначается через [М].
(П1) Открытые множества всякого метрического пространства удовлетворяют аксиомам 1) и 2). Значит всякое метрическое пространство является топологическим пространством.
(П2) Пусть Х – произвольное множество. Будем считать открытыми все его подмножества. Аксиомы 1) и 2) выполняются. Получаем топологическое пространство, в котором любое множество одновременно открыто и замкнуто.
(О) Пусть в одном и том же множестве Х заданы две топологии τ1 и τ2. Будем говорить, что топология τ+1+ сильнее топологии τ2, если система множеств τ1 содержит τ2. Тогда топология τ2 слабее топологии τ1.
(Т1)
Пересечение произвольного множества
топологий (τ=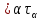 )
в Х является топологией в Х. Эта топология
слабее любой из топологий τα.
(ДОКАЗАТЕЛЬСТВО) Для доказательства
нужно проверить аксиомы 1) и 2). 1)Ясно,
что
)
в Х является топологией в Х. Эта топология
слабее любой из топологий τα.
(ДОКАЗАТЕЛЬСТВО) Для доказательства
нужно проверить аксиомы 1) и 2). 1)Ясно,
что
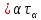 содержит Х и пустое множество. 2)Каждая
из τα
удовлетворяет аксиоме 2): Следовательно
содержит Х и пустое множество. 2)Каждая
из τα
удовлетворяет аксиоме 2): Следовательно
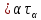 удовлетворяет аксиоме 2). (ДОК)
удовлетворяет аксиоме 2). (ДОК)
№10) Определяющие системы окрестностей.
Задать в пространстве Т топологию – значит указать в нём систему открытых множеств. Однако тогда удобнее задавать не все, а только некоторую систему открытых множеств, по которой однозначно определяются все остальные открытые множества. Например, в метрическом пространстве сначала вводится понятие открытого шара, а затем открытые множества определяют, как такие множества, в которых каждая точка содержится вместе с некоторой своей шаровой окрестностью. Иначе говоря, в метрическом пространстве открыты только те множества, которые представимы как суммы открытых шаров.
Совокупность В открытых подмножеств называется базой топологического пространства Т, если всякое открытое множество в Т представимо как сумма некоторого числа (конечного или бесконечного) множеств из В. Например, совокупность всех открытых шаров – база в метрическом пространстве. Топологию τ топологического пространства Т можно задать, указав в Т некоторую базу В. Не всякая совокупность множеств может быть базой.
Всякая
база в топологическом пространстве
Т=(Х, τ) обладает свойствами: 1)любая точка
х Х
содержится хотя бы в одном множестве
G
Х
содержится хотя бы в одном множестве
G В
(содержится в базе); 2)если точка х
содержится в пересечении множеств G1
и G2,
а G3
В
(содержится в базе); 2)если точка х
содержится в пересечении множеств G1
и G2,
а G3 (G1
(G1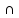 G2).
G2).
(Т1)
Чтобы система В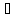 τ была базой данной топологии необходимо
и достаточно, чтобы для каждого открытого
множества G
и для каждой точки x
τ была базой данной топологии необходимо
и достаточно, чтобы для каждого открытого
множества G
и для каждой точки x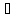 G
существовало такое множество Gx
G
существовало такое множество Gx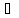 В,
что х
В,
что х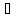 Gx
Gx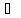 G.
(ДОКАЗАТЕЛЬСТВО) Пусть условия теоремы
выполнены. Тогда всякое открытое
множество G=
G.
(ДОКАЗАТЕЛЬСТВО) Пусть условия теоремы
выполнены. Тогда всякое открытое
множество G=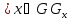 ,
т.е. В – база топологии τ. (Обратно)Пусть
В – база топологии τ. Тогда всякое
открытое множество G
,
т.е. В – база топологии τ. (Обратно)Пусть
В – база топологии τ. Тогда всякое
открытое множество G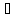 τ представлено в виде суммы множеств
из В. Тогда для каждого х
τ представлено в виде суммы множеств
из В. Тогда для каждого х G
найдётся множество Gx=В
такое, что х
G
найдётся множество Gx=В
такое, что х Gx
Gx G.(ДОК)
G.(ДОК)
Важный класс топологических пространств образуют пространства со счётной базой, т.е. такие, в которых существует хотя бы база, состоящая из счётного числа элементов.
Система
множеств {Mα}
называется покрытием топологического
пространства Т, если Т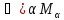 .
Покрытие, состоящее из открытых множеств
является открытым покрытием (из замкнутых
– замкнутым). Если некоторая часть Mβ
покрытия Мα
сама образует покрытие топологического
пространства Т, то Mβ
называется подпокрытием Мα.
.
Покрытие, состоящее из открытых множеств
является открытым покрытием (из замкнутых
– замкнутым). Если некоторая часть Mβ
покрытия Мα
сама образует покрытие топологического
пространства Т, то Mβ
называется подпокрытием Мα.
(Т2)
Если Т – топологическое пространство
со счётной базой, то из всякого его
открытого покрытия можно выбрать
конечное или счётное покрытие.
(ДОКАЗАТЕЛЬСТВО) Путь Mα
– открытое покрытие топологического
пространства Т. Тогда каждая точка х
этого пространства Т содержится в Мα.
Пусть {Gn}
счётная база в Т. Тогда каждый элемент
х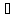 Т
содержится в Gi
Т
содержится в Gi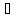 Mα.
Совокупность множеств Gi
конечно или счётно и покрывает всё Т.
Для каждого Gi
выберем одно из содержащих его множеств
Mα,
получим конечное или счётное подпокрытие
Mβ.
(ДОК)
Mα.
Совокупность множеств Gi
конечно или счётно и покрывает всё Т.
Для каждого Gi
выберем одно из содержащих его множеств
Mα,
получим конечное или счётное подпокрытие
Mβ.
(ДОК)
№11) Аксиомы определимости.
Произвольное топологическое пространство представляет собой объект слишком общий с точки зрения мат анализа. Поэтому среди топологических пространств выделяют пространства более близкие по своим свойствам к метрическим пространствам. Для этого к аксиомам 1) и 2) топологическим пространств добавляют какие-нибудь дополнительные условия. Таковым является, например, аксиомы отделимости.
(Аксиома
Т1) (1-я аксиома отделимости) Для любых
2-х различных точек x
и y
топологического пространства Т существует
окрестность Ox
точки х, не содержащее y
и существует окрестность Oy
точки y,
не содержащее точку х. Пространства,
удовлетворяющие аксиоме Т1 называются
Т1 пространствами. В Т1 пространстве
любая точка является замкнутым множеством.
Действительно, если х отлично от y,
то существует окрестность Oy
точки y,
не содержащее х. Это означает, что y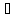 [x],
но тогда [x]=x.
Значит в Т1 пространствах любое конечное
множество точек замкнуто. Любое
метрическое пространство является Т1
пространством.
[x],
но тогда [x]=x.
Значит в Т1 пространствах любое конечное
множество точек замкнуто. Любое
метрическое пространство является Т1
пространством.
(Аксиома
Т2) (Хаусдорф) (Вторая или Хаусдорфова
аксиома отделимости) Любые 2 различные
точки x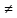 y
топологического пространства Т имеют
пересекающиеся окрестности Ox
и Oy.
Пространство, удовлетворяющее этой
аксиоме, называется Т2 пространством.
Очевидно, что всякое Т2 пространство
является Т1 пространством, но не наоборот.
y
топологического пространства Т имеют
пересекающиеся окрестности Ox
и Oy.
Пространство, удовлетворяющее этой
аксиоме, называется Т2 пространством.
Очевидно, что всякое Т2 пространство
является Т1 пространством, но не наоборот.
Ещё более сильным ограничениям удовлетворяют нормальные пространства. Нормальным пространством называется такое Т1 пространство, в котором любые 2 замкнутых непересекающихся множества имеют непересекающиеся окрестности. К нормальным пространствам относятся все метрические пространства.
№12) Непрерывные отображения топологического пространства.
(О1)
Пусть Х и Y
– 2 топологических пространства.
Отображение f
пространства Х в пространство Y
называется непрерывным в точке x0,
если для любой окрестности Uy0
точки y0=f(x0)
найдётся окрестность Vx0
точки х0
такое, что f(Vx0)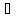 Uy0.
Отображение f:X→Y
называется непрерывным отображением
топологического пространства Х в
числовую прямую, называется функцией,
определённой на Х.
Uy0.
Отображение f:X→Y
называется непрерывным отображением
топологического пространства Х в
числовую прямую, называется функцией,
определённой на Х.
(Т1)
Чтобы отображение f
топологического пространства Х в
топологическое пространство Y
было непрерывно необходимо и достаточно,
чтобы прообраз Г=f—1(G)
всякого открытого множества G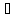 Y
был открыт. (ДОКАЗАТЕЛЬСТВО) (необходимость)
Пусть f
– непрерывное, множество G
открыто в Y.
Нужно доказать, что Г=f—1(G)
открыто в Х. Путь точка х
Y
был открыт. (ДОКАЗАТЕЛЬСТВО) (необходимость)
Пусть f
– непрерывное, множество G
открыто в Y.
Нужно доказать, что Г=f—1(G)
открыто в Х. Путь точка х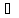 Г,
а f(x)=y.
Тогда y
Г,
а f(x)=y.
Тогда y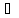 G
и G
является окрестностью точки y.
По определению непрерывности найдётся
такая окрестность Vx
точки x, что f(Vx)
G
и G
является окрестностью точки y.
По определению непрерывности найдётся
такая окрестность Vx
точки x, что f(Vx)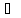 G.
Т.к. Vx
G.
Т.к. Vx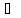 Г.
Иначе говоря, если x
Г.
Иначе говоря, если x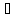 Г,
то найдётся окрестность Vx
точки х такая, что Vx
Г,
то найдётся окрестность Vx
точки х такая, что Vx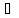 Г.
Значит Г – открытое множество.
(достаточность) Пусть Г=f—1(G)
открыто, если G
открыто. Рассмотрим произвольную точку
х из Г и произвольную окрестность Uy
точки y=f(x).
Т.к. y
Г.
Значит Г – открытое множество.
(достаточность) Пусть Г=f—1(G)
открыто, если G
открыто. Рассмотрим произвольную точку
х из Г и произвольную окрестность Uy
точки y=f(x).
Т.к. y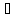 Uy
, то x
Uy
, то x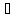 f—1(Uy).
Это множество открыто и является
окрестностью точки х, образ которой
содержится в Uy.
(ДОК)
f—1(Uy).
Это множество открыто и является
окрестностью точки х, образ которой
содержится в Uy.
(ДОК)
(Т2)
Пусть Х,Y,Z
– топологические пространства и пусть
f
и
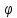 – непрерывные отображения Xf→Yφ.
Тогда отображение
– непрерывные отображения Xf→Yφ.
Тогда отображение
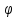 (f(x))
пространства Х в Z
непрерывно.
(f(x))
пространства Х в Z
непрерывно.
(О) Ели отображение f топологического пространства Х на топологическое пространство Y взаимно однозначно и взаимно непрерывно, то оно называется гомеоморфизмом, а пространство Х и Y гомеоморфными.
№13) Компактность.
В мат анализе важную роль играет следующий факт известный под названием Лемма Гейне – Бореля: из любого открытого покрытия [a,b] можно выделить конечное покрытие. Будем отправляться от этого свойства сегмента числовой прямой.
(О1) Топологическое пространство Т называется компактным, если любое его открытое покрытие содержит конечное подпокрытие. Если топологическое пространство Т является компактным и удовлетворяет аксиоме Т2, то оно называется компактом.
Свойствами
компактов обладают наряду с сегментом
числовой прямой все замкнутые ограниченные
множества, пространство Rn.
Однако прямая и плоскость и т.д. служат
простейшими примерами некомпактных
пространств. Назовём некоторую систему
множеств {Aα}
пространства Т центрированной, если
любое конечное пересечение
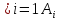 членов этой системы не пусто.
членов этой системы не пусто.
(Т1)
Топологическое пространство компактно
т т т, когда каждая центрированная
система его замкнутых подмножеств имеет
непустое пересечение. (ДОКАЗАТЕЛЬСТВО)
(необходимость) Пусть Т – компактно,
{Fα}
– центрированная система замкнутых
подмножеств множества Т. Тогда множества
Gα=Т
- Fα.
Тогда Gα
открыто. Т.к. любое конечное пересечение
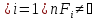 ,
то никакая часть конечной системы
множеств Gi
не покрывает всё Т. Т.к. Т – компактное,
то вся система {Gα}
не образует покрытия Т. Но тогда
,
то никакая часть конечной системы
множеств Gi
не покрывает всё Т. Т.к. Т – компактное,
то вся система {Gα}
не образует покрытия Т. Но тогда
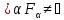 .
(достаточность) Пусть условия теоремы
выполнены. Gα
– открытое покрытие
пространства Т. Положим Т/ Gα=
Fα.
Получим
.
(достаточность) Пусть условия теоремы
выполнены. Gα
– открытое покрытие
пространства Т. Положим Т/ Gα=
Fα.
Получим
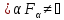 .
Отсюда следует, что система {Fα}
не может быть центрированной. Т.к.
существует конечное число множеств
F1,F2,…,Fn
таких, что
.
Отсюда следует, что система {Fα}
не может быть центрированной. Т.к.
существует конечное число множеств
F1,F2,…,Fn
таких, что
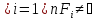 .
Но тогда G1,G2,…,Gn
образует конечное подпокрытие. Значит
Т компактно. (ДОК)
.
Но тогда G1,G2,…,Gn
образует конечное подпокрытие. Значит
Т компактно. (ДОК)
(Т2)
Замкнутое подмножество компактного
пространства компактно. (ДОКАЗАТЕЛЬСТВО)
Пусть F
– замкнутое подмножество компактного
пространства Т. {Fα}
– произвольная центрированная система
замкнутых подмножеств множества F.
Тогда каждая Fα
замкнута и в Т,
т.е. множества Fα-
центрированная система замкнутых
множеств в Т. По (Т1)
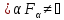 .
Значит F
компактно. (ДОК)
.
Значит F
компактно. (ДОК)
(Следствие) Замкнутое множество компакта есть компакт.
(Т3)
Непрерывное отображение компактного
пространства есть компактное пространство.
(ДОКАЗАТЕЛЬСТВО) Пусть Х – компактное
пространство, X
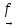 Y
, f
– его отображение на топологическое
пространство Y.
Возьмём произвольное открытое покрытие
пространства Х. Пусть f—1(Vα)=Uα.
Множества Uα
открыты, т.к. f
непрерывно. Множество Uα
образует открытое покрытие пространства
Х. Т.к. Х компактно, то из открытого
покрытия Uα
можно выбрать U1,U2,…,Un.
Но тогда соответствующие множества
V1,…,Vn
покрывают всё Y.
Значит Y
компактно. (ДОК)
Y
, f
– его отображение на топологическое
пространство Y.
Возьмём произвольное открытое покрытие
пространства Х. Пусть f—1(Vα)=Uα.
Множества Uα
открыты, т.к. f
непрерывно. Множество Uα
образует открытое покрытие пространства
Х. Т.к. Х компактно, то из открытого
покрытия Uα
можно выбрать U1,U2,…,Un.
Но тогда соответствующие множества
V1,…,Vn
покрывают всё Y.
Значит Y
компактно. (ДОК)
(Т4)
Если Т – компактное пространство, то
каждое его бесконечное подмножество
имеет хотя бы одну предельную точку.
(ДОКАЗАТЕЛЬСТВО) (от противного) Допустим,
что Т содержит бесконечное подмножество
Х, не имеющее ни одной предельной точки.
Тогда из Х можно выделить счётное
множество Х1={х1,х2,…,хn,…}.
Множество Х 1
тоже не имеет ни одной предельной точки.
Построим множество Х2={х2,…,хn,…},
Х3={х3,…,хn,…},….
Xi
образуют центрированную систему
замкнутых множеств в Т, причём
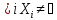 .
Значит Т не компактно. противоречие.
(ДОК)
.
Значит Т не компактно. противоречие.
(ДОК)
№14) Компактность в метрических пространствах.
Т.к.
метрические пространства – частные
случаи топологического пространства,
то на них распространяется компактность.
Для метрических пространств компактность
тесно связана с полной ограниченностью.
Пусть М – некоторое множество в
метрическом пространстве Х. Возьмём
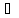 ε>0.
Множество А называется ε сетью для
множества М, если
ε>0.
Множество А называется ε сетью для
множества М, если
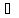 х
х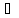 М
найдётся хотя бы одна точка α
М
найдётся хотя бы одна точка α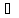 А
такая, что ρ(x,α)<ε.
Множество М называется вполне ограниченным,
если для него существует конечная ε
сеть для
А
такая, что ρ(x,α)<ε.
Множество М называется вполне ограниченным,
если для него существует конечная ε
сеть для
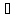 ε>0.
Ясно, что всякое вполне ограниченное
множество является ограниченным
множеством. Обратное не верно. Если М –
вполне ограниченное, то его замыкание
тоже вполне ограниченное. В пространстве
Rn
полная ограниченность совпадает с
ограниченностью. Действительно, если
множество М ограниченно, то оно содержится
в некотором кубе. Разобьём этот куб на
кубки с ребром длины ε. Вершины этих
кубиков образуют конечную ε сеть в
исходном кубе, и тем более в любом
множестве, лежащем внутри куба.
ε>0.
Ясно, что всякое вполне ограниченное
множество является ограниченным
множеством. Обратное не верно. Если М –
вполне ограниченное, то его замыкание
тоже вполне ограниченное. В пространстве
Rn
полная ограниченность совпадает с
ограниченностью. Действительно, если
множество М ограниченно, то оно содержится
в некотором кубе. Разобьём этот куб на
кубки с ребром длины ε. Вершины этих
кубиков образуют конечную ε сеть в
исходном кубе, и тем более в любом
множестве, лежащем внутри куба.
(Т1)Чтобы
метрическое пространство Х было
компактным, необходимо и достаточно
одновременное выполнение условий: 1)
Чтобы Х было вполне ограниченным; 2)Х
являлось полным. (ДОКАЗАТЕЛЬСТВО)
(необходимость полной ограниченности)
(от противного) Допустим, что Х не является
вполне ограниченным. Тогда для некоторого
ε0>0
в Х не существует конечной ε сети. Возьмём
произвольную точку А1
из этого Х. Найдётся хотя бы одна точка
А2
из этого Х такая, что ρ(А1,А2)>
ε0.
Т.к. иначе точка А1
была бы ε0
сетью для Х. Найдётся точка А3
из Х такая, что ρ(А1,А3)>
ε0
и ρ(А2,А3)>
ε0.
Т.к. иначе две точки А1
и А2
составляют ε0
сеть. Продолжая этот процесс, получим
подпоследовательность точек a1,a2,…,an
такую, что ρ(аi,ak)>
ε0
(i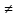 k).
Эта бесконечная последовательность
точек не имеет ни одной предельной
точки. По (Т4) и (Т3) из предыдущего параграфа
Х не компактно. (необходимость полноты)
Пусть Хn
полно, т.е. последовательность Xn
не имеет пределы в Х, т.е. оно не имеет в
Х ни одной предельной точки. По (Т4) из
предыдущего параграфа Х не компактно.
(достаточность) Пусть Х вполне ограниченно
и полно, {Xn}
– произвольная последовательность из
Х. Построим в Х 1-сеть. Вокруг каждой
точки этой 1-сеть построим замкнутый
шар r=1.
Т.к. эти шары покрывают всё Х, а шаров
конечное число, то по крайней мере один
из этих шаров содержит бесконечную
подпоследовательность
k).
Эта бесконечная последовательность
точек не имеет ни одной предельной
точки. По (Т4) и (Т3) из предыдущего параграфа
Х не компактно. (необходимость полноты)
Пусть Хn
полно, т.е. последовательность Xn
не имеет пределы в Х, т.е. оно не имеет в
Х ни одной предельной точки. По (Т4) из
предыдущего параграфа Х не компактно.
(достаточность) Пусть Х вполне ограниченно
и полно, {Xn}
– произвольная последовательность из
Х. Построим в Х 1-сеть. Вокруг каждой
точки этой 1-сеть построим замкнутый
шар r=1.
Т.к. эти шары покрывают всё Х, а шаров
конечное число, то по крайней мере один
из этих шаров содержит бесконечную
подпоследовательность
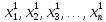 последовательности X1n.
Обозначим этот шар через B1.
В шаре B1
выберем
последовательности X1n.
Обозначим этот шар через B1.
В шаре B1
выберем
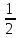 – сеть. Вокруг каждой точки этой сети
построим шар r=
– сеть. Вокруг каждой точки этой сети
построим шар r=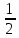 .
По крайней мере один из этих наров
содержит бесконечную подпоследовательность
.
По крайней мере один из этих наров
содержит бесконечную подпоследовательность
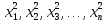 последовательности X2n.
Этот шар обозначим через B2.
Далее найдётся шар В3,
r=
последовательности X2n.
Этот шар обозначим через B2.
Далее найдётся шар В3,
r= ,
содержащий подпоследовательность X3n
и т.д. На ряду с каждым шаром Bn
построим шар An
с тем же центром, но радиус его в 2 раза
больше. Шары An
вложены друг в друга. Т.к. Х полно, то
,
содержащий подпоследовательность X3n
и т.д. На ряду с каждым шаром Bn
построим шар An
с тем же центром, но радиус его в 2 раза
больше. Шары An
вложены друг в друга. Т.к. Х полно, то
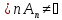 и состоят из единственной точки х0.
Эта точка является предельной точкой
для последовательности Xn.
Т.к. любая окрестность точки содержит
некоторый шар Bk,
а значит и бесконечную подпоследовательность
{
и состоят из единственной точки х0.
Эта точка является предельной точкой
для последовательности Xn.
Т.к. любая окрестность точки содержит
некоторый шар Bk,
а значит и бесконечную подпоследовательность
{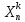 }
нашей последовательности Xn.
(ДОК)
}
нашей последовательности Xn.
(ДОК)
№15) Действительные функции на метрических и топологических пространствах.
Действительной
функцией на топологическом (метрическом)
пространстве Т называется отображение
пространства Т в числовую прямую. Если
функция задана на метрическом пространстве,
то имеет смысл понятие равномерной
непрерывности. Функция f(x)
называется равномерно непрерывной на
на метрическом пространстве Х, если
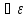 >0
>0
 δ>0
такое, что если ρ(x1,x2)<δ,
то |f(x1),f(x2)|<ε.
δ>0
такое, что если ρ(x1,x2)<δ,
то |f(x1),f(x2)|<ε.
(Т1)Если
действительная функция непрерывна на
метрическом компакте, то она равномерно
непрерывна. (ДОКАЗАТЕЛЬСТВО) Допустим,
что f(x)
непрерывна, но не равномерно непрерывна
на компакте К. Тогда для некоторого ε>0
и для любого натурального n
найдутся в K
точки xn
и
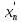 такие, что ρ(xn,
такие, что ρ(xn,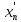 )<
)<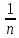 ,
но |f(xn),f(
,
но |f(xn),f(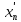 )|≥ε.
Т.к. К – компакт, то из последовательности
{xn}
можно выбрать последовательность {
)|≥ε.
Т.к. К – компакт, то из последовательности
{xn}
можно выбрать последовательность {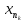 },
сходящуюся к некоторой точке х
},
сходящуюся к некоторой точке х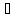 К.
Тогда и соответствующая подпоследовательность
{
К.
Тогда и соответствующая подпоследовательность
{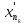 }
сходится к х. Однако для каждого К должно
выполнятся хотя бы одно из неравенств
|f(
}
сходится к х. Однако для каждого К должно
выполнятся хотя бы одно из неравенств
|f(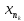 ),f(х)|≥
),f(х)|≥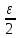 и |f(
и |f( ),f(х)|≥
),f(х)|≥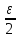 .
А это противоречит непрерывности функции
f(x)
в точке х. (ДОК)
.
А это противоречит непрерывности функции
f(x)
в точке х. (ДОК)
(Т2) Пусть Т – компактное пространство, f – непрерывная в нём функция. Тогда f ограниченна на Т и достигает на Т верхней и нижней граней. (ДОКАЗАТЕЛЬСТВО) Непрерывная функция есть непрерывное отображения пространства Т в числовую прямую. По (Т3) параграфа 13 образ Т компактен, а компактное подмножество числовой прямой замкнуто и ограничено и потому имеет верхнюю и нижнюю грани и содержит их. (ДОК)
№16) Линейные пространства.
(О1) Непустое множество L элементов x,y,z,… называется линейным или векторным пространством, если оно удовлетворяет аксиомам:
