
Funktsionalny_analiz
.docx1) Определение и примеры метрических пространств.
(О1) Метрическим пространством называется пара (X,ρ), состоящая из множества X элементов и однозначной неотрицательной действительной функции ρ(x,y), определённой для всех х из Х, называемой расстоянием или метрикой и удовлетворяющее условиям (аксиомам): 1) ρ(x,y)=0 т т т, x=y; 2) ρ(x,y)= ρ(y,x); 3) ρ(x,z)≤ ρ(x,y)+ ρ(y,z).
(П1) Множество действительных чисел с расстоянием ρ(x,y)=|x-y| образует метрическое пространство R.
(П2)
Множество упорядоченных групп из n
действительных чисел x=(x1
, … , xn)
с расстоянием ρ(x,y)=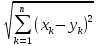 (1) называется n-мерным
Евклидовым пространством Rn.
Проверка аксиом: справедливость аксиом
1) и 2) очевидна. Осталось проверить
аксиому 3). Пусть x=(x1
, … , xn),
y=(y1
, … , yn),
z=(z1
, … , zn).
Нужно доказать
(1) называется n-мерным
Евклидовым пространством Rn.
Проверка аксиом: справедливость аксиом
1) и 2) очевидна. Осталось проверить
аксиому 3). Пусть x=(x1
, … , xn),
y=(y1
, … , yn),
z=(z1
, … , zn).
Нужно доказать
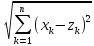 ≤
≤
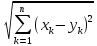 +
+
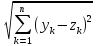 (2). Положим xk-yk
=ak,
yk-zk
=bk.Тогда
xk-zk
=ak+bk.
Значит равенство (2) примет вид:
(2). Положим xk-yk
=ak,
yk-zk
=bk.Тогда
xk-zk
=ak+bk.
Значит равенство (2) примет вид:
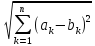 ≤
≤
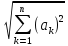 +
+
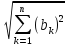 (3). Воспользуемся неравенством
Коши-Буняковского (|(x,y)|≤||x||*||y||):
(3). Воспользуемся неравенством
Коши-Буняковского (|(x,y)|≤||x||*||y||):
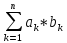 ≤
≤
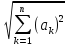 *
*
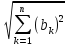 .
Из (3) имеем
.
Из (3) имеем
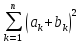 =
=
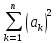 +
+
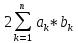 +
+
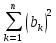 ≤
≤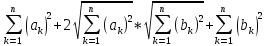 =
=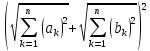 .
Т.е. аксиома доказана.
.
Т.е. аксиома доказана.
(П3)То
же множество упорядоченных групп из n
действительных чисел x=(x1
, … , xn),
расстояние ρ(x,y)=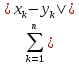 (4). Справедливость всех аксиом очевидна.
Это метрическое пространство обозначают
через
(4). Справедливость всех аксиом очевидна.
Это метрическое пространство обозначают
через
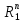 .
.
(П4)То
же множество, что и в примерах 2 и 3,
расстояние ρ0(x,y)=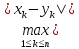 .
Справедливость всех аксиом очевидна.
.
Справедливость всех аксиом очевидна.
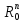 .
.
(П5)Множество
всех непрерывных функций, оределённых
на сегменте [a,b]
с расстоянием ρ(x,y)=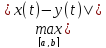 (5). Аксиомы 1 и 2 очевидны. Аксиома 3:
ρ(x,z)=
(5). Аксиомы 1 и 2 очевидны. Аксиома 3:
ρ(x,z)=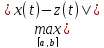 =
=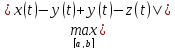 ≤
≤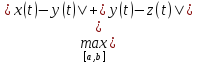 ≤
≤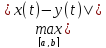 +
+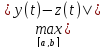 =
ρ(x,y)+
ρ(y,z).Метрическое
пространство обозначается через C[a,b].
=
ρ(x,y)+
ρ(y,z).Метрическое
пространство обозначается через C[a,b].
(П6)Множество
всех последовательностей x=(x1
, … , xn)
действительных чисел, удовлетворяющих
условию
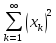 <
<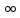 сходится с расстоянием ρ(x,y)=
сходится с расстоянием ρ(x,y)=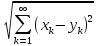 (6).
(6).
Функция
ρ(x,y)
имеет смысл при всех x
и y,
удовлетворяющих условию
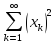 сходится
и
сходится
и
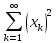 тоже
сходится. Действительно, из неравенства
(xk-yk)2≤2(xk+yk)2
следует, что
тоже
сходится. Действительно, из неравенства
(xk-yk)2≤2(xk+yk)2
следует, что
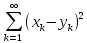 сходится.
Значит (6) имеет смысл при таких условиях.
Аксиомы 1) и 2) очевидны. Аксиома 3) принимает
вид:
сходится.
Значит (6) имеет смысл при таких условиях.
Аксиомы 1) и 2) очевидны. Аксиома 3) принимает
вид: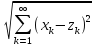 ≤
≤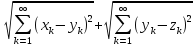 (7).
Каждый из этих рядов сходится при любом
натуральном n.
Справедливо :
(7).
Каждый из этих рядов сходится при любом
натуральном n.
Справедливо :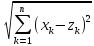 ≤
≤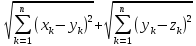 .
Переходя здесь к пределу при n→
.
Переходя здесь к пределу при n→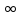 ,
получим (7). Это метрическое пространство
обозначают через
,
получим (7). Это метрическое пространство
обозначают через
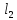 .
.
(П7)
Совокупность всех непрерывных функций,
определённых на [a,b]
с расстоянием ρ(x,y)=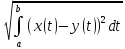 .
Получим метрическое пространство
непрерывных функций с квадратичной
метрикой. Обозначается через C2[a,b].
.
Получим метрическое пространство
непрерывных функций с квадратичной
метрикой. Обозначается через C2[a,b].
(П8)
Множество всех ограниченных
последовательностей x=(x1
, … , xn)
с расстоянием ρ(x,y)=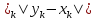 .Полученное
метрическое пространство обозначается
через m.
.Полученное
метрическое пространство обозначается
через m.
(П9)Множество
упорядоченных групп, состоящих из n
действительных чисел x=(x1
, … , xn)
с расстоянием ρ(x,y)=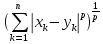 ,
где p≥1
– любое действительное число. Метрическое
пространство обозначается через
,
где p≥1
– любое действительное число. Метрическое
пространство обозначается через
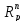 .
.
(П10)Множество
всех последовательностей, удовлетворяющих
условию
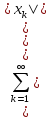 <
<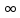 ,
p≥1
– действительное число. ρ(x,y)=
,
p≥1
– действительное число. ρ(x,y)=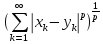 .
Обозначается через
.
Обозначается через
 .
.
Пусть M=(X, ρ)- метрическое пространство, P – любое подмножество множества X. Тогда P с той же метрикой ρ(x,y) тоже является метрическим пространством, которое называется подпространством метрического пространства M.
№2) Сходимость. Непрерывные отображения метрических пространств.
Последовательность
x1
, … , xn,…
в метрическом пространстве X
сходится к точке x,
если любая окрестность
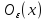 все точки xn,
начиная с некоторой, т.е.
все точки xn,
начиная с некоторой, т.е.
 >0
>0
 N=N(
N=N(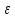 )
такой, что
)
такой, что
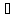 n>N
будет xn
n>N
будет xn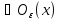 .
Точка х называется пределом
последовательности {xn}.
.
Точка х называется пределом
последовательности {xn}.
Это
можно сформулировать иначе:
последовательность {xn}
сходится к x,
если
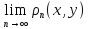 =0.
=0.
Итак, понятие предела последовательности в метрическом пространстве (X, ρ) свелось к понятию предела последовательности действительных чисел. Но тогда непосредственно из определения вытекает в частности, что в метрическом пространстве: 1)Последовательность {xn} не может иметь более одного предела; 2)Если {xn} сходится к x, то любая её подпоследовательность сходится к х.
Пусть
задано отображение f
метрического пространства (X,
ρ) в метрическое
пространство (Y,
ρ1).
Отображение y=f(x)
называется непрерывным в точке x0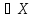 ,если
,если
 xn
xn xn
сходится к x0,
последовательность {yn},
где yn=f(xn),
сходится к точке y0=f(x0),
x0
xn
сходится к x0,
последовательность {yn},
где yn=f(xn),
сходится к точке y0=f(x0),
x0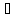 Х,
y0
Х,
y0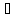 Y.
Y.
Это
определение эквивалентно следующему:
отображение y=f(x)
называется непрерывным в точке x0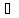 X,
если
X,
если
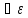 >0
>0
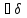 >0
такое, что
>0
такое, что
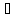 x
x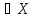 , удовлетворяющего
условиям ρ(x,x0)<
, удовлетворяющего
условиям ρ(x,x0)<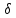 ,
выполняется неравенство ρ1(f(x),f(x0))<
,
выполняется неравенство ρ1(f(x),f(x0))<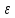 .
.
Если отображение f непрерывно во всех точках пространства Х, то говорят, что f непрерывна на X.
Если f отображает X на Y взаимно однозначно, то существует обратное отображение x=f—1(y) пространства Y на X.
Если f взаимно однозначна и взаимно непрерывна, то оно называется гомеоморфным отображением или гомеоморфизмом.
Метрические
пространства X
и Y,
между которыми можно установить
гомеоморфное отображение, называются
гомеоморфными. Например, вся числовая
прямая R
и интервал (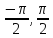 )
гомеоморфны. Гомеоморфизм устанавливается
формулой y=arctg
x.
)
гомеоморфны. Гомеоморфизм устанавливается
формулой y=arctg
x.
Частный
случай гомеоморфизма – изометрическое
отображение метрических пространств.
Взаимно однозначное отображение f
метрического пространства (X,
ρ) на метрическое
пространство (Y,
ρ1)
называется изометрическим, если ρ(x1,x2)=
ρ1(f(x1),f(x2))
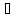 x1,
x1,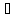 x2.
x2.
Пространства, между которыми можно установить изометрическое соответствие, называются изометричными. В дальнейшем такие пространства будем считать как тождественные.
(Т1)
Отображение f
метрического пространства X
в метрическое пространство Y
непрерывно на X
т т т, когда множество f—1(v)
открыто в Х для любого открытого множества
V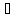 Y.
(ДОКАЗАТЕЛЬСТВО) Пусть f
непрерывно на Х, V
– открытое множество в Y.
Нужно доказать, что каждая точка множества
f—1(v)
является его внутренней точкой, т.е.
принадлежит ему вместе со своей
окрестностью. Пусть p
Y.
(ДОКАЗАТЕЛЬСТВО) Пусть f
непрерывно на Х, V
– открытое множество в Y.
Нужно доказать, что каждая точка множества
f—1(v)
является его внутренней точкой, т.е.
принадлежит ему вместе со своей
окрестностью. Пусть p X,
а f(p)
X,
а f(p) V.
Т.к. V
открыто, то
V.
Т.к. V
открыто, то
 >0
такое, что если ρ1(f(p),y)<
>0
такое, что если ρ1(f(p),y)<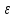 ,
то y
,
то y V.
Т.к. f
непрерывно в точке p,
то для этого
V.
Т.к. f
непрерывно в точке p,
то для этого
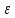 найдётся δ>0 такое, что если ρ(p,X)<δ,
то ρ1(f(p),f(x))<ε.
Это означает, что если ρ(p,X)<δ,
то x
лежит в f—1(v).
Значит множество f—1(v)
– открыто. (Обратно) Пусть f—1(v)
открыто для любого открытого множества
V
из Y.
Зафиксируем точку p
из метрического пространства X
и возьмём произвольное ε>0. Множество
всех точек y
из Y,
удовлетворяющее условию ρ1(y,f(p))<ε,
обозначим через V.
Это множество открыто, так как f—1(v)
открыто. Поэтому существует δ>0 такое,
что если ρ(p,x)<δ,
то x
найдётся δ>0 такое, что если ρ(p,X)<δ,
то ρ1(f(p),f(x))<ε.
Это означает, что если ρ(p,X)<δ,
то x
лежит в f—1(v).
Значит множество f—1(v)
– открыто. (Обратно) Пусть f—1(v)
открыто для любого открытого множества
V
из Y.
Зафиксируем точку p
из метрического пространства X
и возьмём произвольное ε>0. Множество
всех точек y
из Y,
удовлетворяющее условию ρ1(y,f(p))<ε,
обозначим через V.
Это множество открыто, так как f—1(v)
открыто. Поэтому существует δ>0 такое,
что если ρ(p,x)<δ,
то x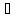 f—1(v).
Но тогда f(x)
f—1(v).
Но тогда f(x)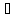 V,
т.е. ρ1(f(p),f(x))<ε.
Значит f
непрерывна в точке p,
а значит и на всём X.
(ДОК)
V,
т.е. ρ1(f(p),f(x))<ε.
Значит f
непрерывна в точке p,
а значит и на всём X.
(ДОК)
Отображение
f
метрического пространства X
в метрическое пространство Y
называется равномерно непрерывным,
если
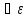 >0
>0
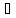 δ>0
такое, что если ρ(x1,x2)<δ,
то ρ1(f(x1),f(x2))<ε.
Если f
равномерно непрерывно, то оно непрерывно.
Обратное не верно.
δ>0
такое, что если ρ(x1,x2)<δ,
то ρ1(f(x1),f(x2))<ε.
Если f
равномерно непрерывно, то оно непрерывно.
Обратное не верно.
№3)Связность. Плотные подмножества.
Метрическое
пространство X
называется несвязным, если его возможно
представить в виде суммы 2-x
непересекающихся непустых замкнутых
множеств: X=Ф1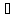 Ф2.
Т.к. Ф1
и Ф2
взаимодополнительны до Х, то каждое из
них как дополнение к замкнутому множеству
является открытым множеством. Так что
в определении несвязности множества
Ф1
и Ф2
можем считать открытыми. Такие множества
называются открыто замкнутыми. Если
при всяком представлении метрического
пространства Х в виде 2-х непересекающихся
замкнутых множеств по крайней мере одно
из них пусто, то Х называется связным.
Можно доказать, что множество М
Ф2.
Т.к. Ф1
и Ф2
взаимодополнительны до Х, то каждое из
них как дополнение к замкнутому множеству
является открытым множеством. Так что
в определении несвязности множества
Ф1
и Ф2
можем считать открытыми. Такие множества
называются открыто замкнутыми. Если
при всяком представлении метрического
пространства Х в виде 2-х непересекающихся
замкнутых множеств по крайней мере одно
из них пусто, то Х называется связным.
Можно доказать, что множество М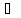 R
связно т т т, когда M
– одно из множеств: сегмент, интервал,
полуинтервал (конечные или бесконечные).
Примерами несвязных множеств могут
служить сумма сегментов или интервалов
без общих точек. Открытое связное
множество называется областью.
R
связно т т т, когда M
– одно из множеств: сегмент, интервал,
полуинтервал (конечные или бесконечные).
Примерами несвязных множеств могут
служить сумма сегментов или интервалов
без общих точек. Открытое связное
множество называется областью.
(Т1)Если метрическое пространство Х связно, то непрерывное отображение f метрического пространства Х в метрическое пространство Y связно: f(X) связно.(ДОКАЗАТЕЛЬСТВО)(от противного) Допустим, что f(x) несвязно. Тогда f(X)=Ф1 или Ф2 , где Ф1 и Ф2 непустые открытые непересекающиеся множества. По (Т1) предыдущего параграфа их прообразы F1 и F2 – непустые открытые множества без общих точек, дающие в сумме Х. Следовательно Х несвязно. противоречие. (ДОК)
Пусть
А и В - два множества в метрическом
пространстве Х. Множество А называется
плотным в В, если B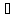 [A].
В частности множество А называется
всюду плотным, если [A]=X.
Например, множество рациональных чисел
всюду плотно на числовой прямой R.
Множество А называется нигде не плотным,
если оно не плотно ни в одном шаре. Если
метрическое пространство Х имеет
счётное, всюду плотное, множество, то
оно называется сепарабельным.
[A].
В частности множество А называется
всюду плотным, если [A]=X.
Например, множество рациональных чисел
всюду плотно на числовой прямой R.
Множество А называется нигде не плотным,
если оно не плотно ни в одном шаре. Если
метрическое пространство Х имеет
счётное, всюду плотное, множество, то
оно называется сепарабельным.
Все
пространства, указанные в примерах 1-7
из параграфа 1, сепарабельные: 1)В R
– рациональные точки счётное всюду
плотное множество; 2)3)4) – векторы с
рациональными координатами; 5)В C[a,b]
– многочлены с рациональными
координатами;6)В
 2
– последовательности с рациональными
членами; 7)В C2[a,b]-
многочлены с рациональными коэффициентами;
8)Метрическое пространство М не
сепарабельно.
2
– последовательности с рациональными
членами; 7)В C2[a,b]-
многочлены с рациональными коэффициентами;
8)Метрическое пространство М не
сепарабельно.
№4)Плотные метрические пространства.
Последовательность
{xn}
метрического пространства Х называется
фундаментальной, ели она удовлетворяет
условию Коши, т.е.
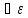 >0
>0
 N=N(
N=N(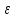 )
такой, что ρ(xn,xm)<ε,
если n>N,
n>M.
Фундаментальная последовательность
называется сходящейся в себе
последовательностью. Всякая сходящаяся
последовательность является
фундаментальной. Действительно, пусть
xn→x.
Тогда
)
такой, что ρ(xn,xm)<ε,
если n>N,
n>M.
Фундаментальная последовательность
называется сходящейся в себе
последовательностью. Всякая сходящаяся
последовательность является
фундаментальной. Действительно, пусть
xn→x.
Тогда
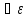 >0
найдётся номер N=N(ε)
такой, что ρ(xn,x)<
>0
найдётся номер N=N(ε)
такой, что ρ(xn,x)<
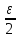 ,
если n>N.
Тогда ρ(xn,xm)≤
ρ(xn,x)
+ ρ(x,xm)<
,
если n>N.
Тогда ρ(xn,xm)≤
ρ(xn,x)
+ ρ(x,xm)<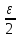 +
+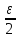 =ε,
если n>N,m>N.
Обратное имеет место не всегда, т.е. не
всякая функциональная последовательность
сходится.
=ε,
если n>N,m>N.
Обратное имеет место не всегда, т.е. не
всякая функциональная последовательность
сходится.
Если в метрическом пространстве Х любая функциональная последовательность сходится, то это пространство Х называется полным метрическим пространством. Можно доказать, что все метрические пространства из параграфа 1 являются полными, кроме пространства C2[a,b]. Докажем полноту пространств R, Rn, C[a,b].
(П1)Путь Х=R. Для множества действительных чисел справедлив критерий Коши: если последовательность {xn} действительных чисел удовлетворяет условию|xn-xm|<ε при n>N,m>m, то последовательность {xn} сходится (имеет предел). Следовательно любая функциональная последовательность действительных чисел сходится, т.е. R – полное метрическое пространство.
(П2)Пусть
Х=Rn.
Воспользуемся полнотой пространства
R.
Пусть Последовательность {x(p)}
– функциональная последовательность
из Rn,
т.е.
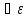 >0
>0
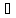 N=N(
N=N(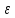 )
такой, что ρ(x(p),x(q))
=
)
такой, что ρ(x(p),x(q))
=
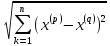 <ε
при p>N,
q>N.
Отсюда следует, что последовательность
{
<ε
при p>N,
q>N.
Отсюда следует, что последовательность
{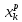 }
является функциональной последовательностью
действительных чисел. Из предыдущего
примера имеем
}
является функциональной последовательностью
действительных чисел. Из предыдущего
примера имеем
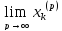 =xk.
Обозначим точки с коэффициентами
(x1,x2,…,xn)=x.
Тогда
=xk.
Обозначим точки с коэффициентами
(x1,x2,…,xn)=x.
Тогда
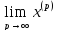 =x
=x Rn.
Таким образом Rn
– полное метрическое пространство.
Rn.
Таким образом Rn
– полное метрическое пространство.
(П3)Пусть
Х=C[a,b].
Пусть {xn(t)}
– функциональная последовательность
в C[a,b],
т.е.
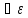 >0
>0
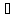 N=N(
N=N(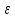 )
такой, что
)
такой, что
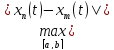 <ε,
если n>N,
m>N.
Отсюда следует, что |xn(t)-xm(t)|<ε
при n>N,
m>N,
<ε,
если n>N,
m>N.
Отсюда следует, что |xn(t)-xm(t)|<ε
при n>N,
m>N,
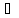 t
t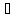 [a,b].
Но тогда предел x(t)
является непрерывной на [a,b]
функцией. Устремим m→
[a,b].
Но тогда предел x(t)
является непрерывной на [a,b]
функцией. Устремим m→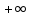 .
Получим
.
Получим
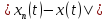 <ε при n>N.
Значит
<ε при n>N.
Значит
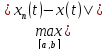 <ε
при n>N.
Следовательно ρ(xn,x)→0
при n→
<ε
при n>N.
Следовательно ρ(xn,x)→0
при n→ ,
т.е. C[a,b]
– полное пространство.
,
т.е. C[a,b]
– полное пространство.
№5)Принцип вложенных шаров.
В математическом анализе широко используется принцип сжимающихся отрезков. В метрических пространствах аналогичную роль играет принцип вложенных шаров.
(T1)Для
того, чтобы метрическое пространство
Х было полным, необходимо и достаточно,
чтобы в нём всякая последовательность
вложенных друг в друга замкнутых шаров,
радиусы которых →0, имело непустое
пересечение.(ДОКАЗАТЕЛЬСТВО)(необходимость)
Пусть Х является полным. В1,
В2,
… поcледовательность
вложенным друг в друга замкнутых шаров.
Шар Bn
имеет центр в xn
и радиус rn
→0. Нужно доказать, что
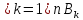 не пусто. Последовательность {xn}
фундаментальна, так как при m>n
ρ(xn,xm)<rn→0.
Т.к. Х является полным, то
не пусто. Последовательность {xn}
фундаментальна, так как при m>n
ρ(xn,xm)<rn→0.
Т.к. Х является полным, то
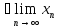 =х
=х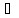 Х.
Покажем, что х
Х.
Покажем, что х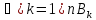 .
Действительно, шар Bn
содержит все точки последовательности
{xn},
кроме быть может x1,…,xn-1.
Значит х является предельной точкой
для шара Bn.
Т.к. Bn
замкнут, то x
.
Действительно, шар Bn
содержит все точки последовательности
{xn},
кроме быть может x1,…,xn-1.
Значит х является предельной точкой
для шара Bn.
Т.к. Bn
замкнут, то x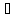 Bn.
Тогда х
Bn.
Тогда х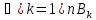 ,т.е.
,т.е.
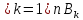 не пусто. (необходимость) Пусть
последовательность {xn}
является фундаментальной. Покажем, что
она имеет предел х
не пусто. (необходимость) Пусть
последовательность {xn}
является фундаментальной. Покажем, что
она имеет предел х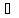 Х.
В силу фундаментальности из
последовательности {xn}
можно выбрать точку
Х.
В силу фундаментальности из
последовательности {xn}
можно выбрать точку
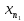 так, что ρ(xn,
так, что ρ(xn,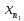 )<
)<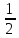
 n>n1.
Возьмём точку Возьмём точку
n>n1.
Возьмём точку Возьмём точку
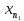 за центр замкнутого шара радиуса 1,
который обозначим через R1.
Затем выберем точку
за центр замкнутого шара радиуса 1,
который обозначим через R1.
Затем выберем точку
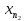 из
{xn}
так, чтобы n2>n1
и ρ(xn,
из
{xn}
так, чтобы n2>n1
и ρ(xn,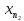 )
<
)
<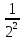
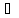 n>n2.
Примем
n>n2.
Примем
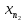 за центр замкнутого шара радиуса
за центр замкнутого шара радиуса
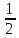 ,
который обозначим через R2.
И так далее. Продолжая процесс
неограниченно, получим последовательность
замкнутых шаров R1,R2,…,Rk
вложенных друг в друга. Эта последовательность
шаров имеет общую точку x,
которая является пределом
подпоследовательности {
,
который обозначим через R2.
И так далее. Продолжая процесс
неограниченно, получим последовательность
замкнутых шаров R1,R2,…,Rk
вложенных друг в друга. Эта последовательность
шаров имеет общую точку x,
которая является пределом
подпоследовательности {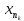 }
последовательности {xn}.
Но если функциональная последовательность
{xn}
содержит сходящуюся подпоследовательность
{
}
последовательности {xn}.
Но если функциональная последовательность
{xn}
содержит сходящуюся подпоследовательность
{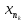 },
то она сама сходится к тому же пределу.
Значит
},
то она сама сходится к тому же пределу.
Значит
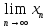 =х
=х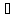 Х.
(ДОК)
Х.
(ДОК)
№6)Теорема Бэра.
В теории полным метрических пространств большую роль играет теорема Бэра.
(Т1)(Теорема
Бэра)Полное метрическое пространство
Х не может быть представлено в виде
объединения счётного числа нигде не
плотных множеств. (ДОКАЗАТЕЛЬСТВО) (от
противного) Допустим, что Х=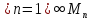 ,
где каждое из множеств Mn
нигде не плотно. Пусть S0
– замкнутый шар радиуса 1. Т.к. М1
нигде не плотно, то оно не плотно в S0.
Поэтому существует замкнутый шар S1
радиуса <
,
где каждое из множеств Mn
нигде не плотно. Пусть S0
– замкнутый шар радиуса 1. Т.к. М1
нигде не плотно, то оно не плотно в S0.
Поэтому существует замкнутый шар S1
радиуса <
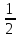 такой, что S1
такой, что S1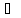 S0,
S1
S0,
S1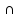 M1=
M1= .
Т.к. M2
нигде не плотно, то M2
не плотно в S1.
Значит в S
найдётся замкнутый шар радиуса <
.
Т.к. M2
нигде не плотно, то M2
не плотно в S1.
Значит в S
найдётся замкнутый шар радиуса <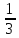 , для которого S2
, для которого S2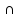 M2=
M2= и т.д. Продолжая процесс неограниченно,
получим последовательность вложенных
друг в друга замкнутых шаров {Sn},
радиусы которых →0, причём Sn
и т.д. Продолжая процесс неограниченно,
получим последовательность вложенных
друг в друга замкнутых шаров {Sn},
радиусы которых →0, причём Sn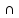 Mn=
Mn=
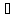 n.
По принципу вложенных друг в друга
замкнутых шаров
n.
По принципу вложенных друг в друга
замкнутых шаров
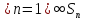 не пусто, т.е. содержит некоторую точку
х
не пусто, т.е. содержит некоторую точку
х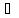 Х.
Однако эта точка х по построению не
принадлежит ни одному из множеств Mn,
т.е. х
Х.
Однако эта точка х по построению не
принадлежит ни одному из множеств Mn,
т.е. х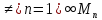 .
Х
.
Х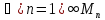 ,
что противоречит нашему предположению.
(ДОК)
,
что противоречит нашему предположению.
(ДОК)
Если метрическое пространство Х не является полным, то его всегда можно включить некоторым способом в полное метрическое пространство.
(О1)Пусть Х – метрическое пространство. Полное метрическое X* называется пополнением метрического пространства Х, если: 1)Х является подпространством пространства Х*; 2)Х всюду плотно в Х*, т.е. [X]=Х*. Например множество всех действительных чисел является пополнением пространства рациональных чисел.
№7)Принцип сжимающих отображений.
Пусть Х – метрическое пространство.
(O1)Отображение
А метрического пространства Х в себя
называется сжимающим отображением,
если
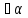 ,
0<α<1 такое, что
,
0<α<1 такое, что
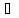 x,y
x,y Х
выполняется неравенство ρ(∆x,∆y)≤αρ(x,y)
(1).
Х
выполняется неравенство ρ(∆x,∆y)≤αρ(x,y)
(1).
Всякое сжимающее отображение является непрерывным. Действительно, пусть xn →x, ρ(xn,x)→0. Из (1) видим, что ρ(Axn,Ax)→0.
Точка х называется неподвижной точкой отображения А, если Ах=х. Иначе говоря, неподвижная точка – решение уравнения Ах=х.
(Т1)
(Теорема Банаха) (Принцип сжимающих
отображений) Всякое сжимающее отображение,
определённое в полном метрическом
пространстве Х, имеет одну и только одну
неподвижную точку.(Т.е. уравнение f(x)=x
имеет единственное решение) (ДОКАЗАТЕЛЬСТВО)
Пусть х0
произвольная точка метрического
пространства Х, f(x0)=x1,
f(x1)=f(f(x0))=f2(x0)=x2,
f(x2)=f(f(f(x0)))=f3(x0)
и так далее. Получим последовательность
x0,x1,…,xn,…
, где xn=fn(x0).
Покажем, что эта последовательность
фундаментальна. Для определённости
положим, что m>n.
ρ(xn,xm)=ρ(fn(x0),fm(x0))≤αnρ(x0,fm-n(x0))=αnρ(x0,xm-n)≤
αn(ρ(x0,x1)+
ρ(x1,xm-n))≤
αn(ρ(x0,x1)+
ρ(x1,x2)+
ρ(x2,xm-n))
≤ αn(ρ(x0,x1)+
ρ(x1,x2)+
ρ(x2,x3)+
ρ(x3,xm-n))≤
αn(ρ(x0,x1)+
ρ(x1,x2)+
ρ(x2,x3)+
…+ ρ(xm-n-1,xm-n))=
αn(ρ(x0,x1)+
ρ(f(x0),f(x1))+
ρ(f2(x0),f2(x1))+…+
ρ(fm-n-1(x0),fm-n-1(x1)))≤
αn(ρ(x0,x1)+
αρ(x0,x1)+
α2ρ(x0,x1)+…+αm-n-1ρ(xm-n-1,xm-n))=αnρ(x0,x1)(1+α+α2+…+αm-n-1)≤
αnρ(x0,x1)(1+α+α2+…+αm-n-1+…)=
αnρ(x0,x1)
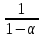 .
Т.к. 0<α<1,
то αn→0
при n→
.
Т.к. 0<α<1,
то αn→0
при n→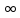 .
Значит при достаточно большом n
полученное выражение как годно мало,
т.е. последовательность {xn}
фундаментальна. Т.к. метрическое
пространство Х является полным, то
последовательность {xn}
сходится в Х, т.е.
.
Значит при достаточно большом n
полученное выражение как годно мало,
т.е. последовательность {xn}
фундаментальна. Т.к. метрическое
пространство Х является полным, то
последовательность {xn}
сходится в Х, т.е.
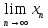 =х
=х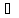 Х.
Т.к. отображение f
непрерывно, то f(x)=f(
Х.
Т.к. отображение f
непрерывно, то f(x)=f(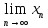 )=
)=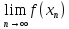 =
=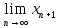 =х.
Т.о. неподвижная точка существует.
Осталось доказать её единственность.
Допустим, что f(x)=x
и f(y)=y.
Тогда ρ(f(x),f(y))≤αρ(x,y),
т.е. ρ(x,y)≤α(x,y),
ρ(x,y)(1-α)≤0.
Т.к. 0<α<1,
то ρ(x,y)≤0
=> ρ(x,y)=0.
(ДОК)
=х.
Т.о. неподвижная точка существует.
Осталось доказать её единственность.
Допустим, что f(x)=x
и f(y)=y.
Тогда ρ(f(x),f(y))≤αρ(x,y),
т.е. ρ(x,y)≤α(x,y),
ρ(x,y)(1-α)≤0.
Т.к. 0<α<1,
то ρ(x,y)≤0
=> ρ(x,y)=0.
(ДОК)
Принцип сжимающих отображений исключительно широко применяется в доказательствах существования и единственности, решений уравнений различных типов. Кроме того, он даёт метод приближённого нахождения этих решений – метод последовательных приближений или метод итераций. Рассмотрим некоторые примеры.
I Алгебраические уравнения.
Пусть f(x) – функция, определенная на сегменте [a,b] и удовлетворяющая условию Липшица lf(x1)-f(x2)l≤K*lx1-x2l с постоянной K<1 и отображающая [a,b] в себя. Тогда f – сжимающее отображение. По теореме 1 последовательность x0, f(x0), f(f(x0)), …, сходится к единственному корню уравнения f(x)=x. В частности условие сжимаемости будет выполняться, если f(x) на [a,b] имеет производную f’(x), причём lf(x)l≤K<1.
Пусть
нужно решить уравнение F(x)=0,
x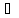 [a,b].
Пусть F(a)<0,
F(b)>0.
Пусть 0<K1≤F’(x)≤K2.
Введём функцию f(x)=x-λF(x)
и будем решать уравнение f(x)=x,
которое равносильно уравнению f(x)=0
при λ
[a,b].
Пусть F(a)<0,
F(b)>0.
Пусть 0<K1≤F’(x)≤K2.
Введём функцию f(x)=x-λF(x)
и будем решать уравнение f(x)=x,
которое равносильно уравнению f(x)=0
при λ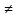 0.f’(x)=1-λF(x),
отсюда 1-λK2≤f’(x)≤1-λK1.
Отсюда подбираем число λ
так, чтобы можно было использовать метод
последовательных приближений.
0.f’(x)=1-λF(x),
отсюда 1-λK2≤f’(x)≤1-λK1.
Отсюда подбираем число λ
так, чтобы можно было использовать метод
последовательных приближений.
II Решение линейных систем.
Рассмотрим
отображение A
n-мерного
пространства в себя, задаваемая системой
линейных уравнений yi=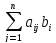 (i=
(i=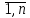 )
)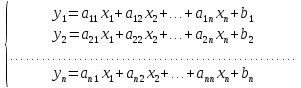
 y1=(y11,y12,…,y1n)
y1=(y11,y12,…,y1n)
Если А – сжимающее отображение, то можно применить метод последовательных приближений (итерации) к уравнению Ax=x. При каких условиях отображение А будет сжимающим? Ответ на этот вопрос зависит от метрики в пространстве. Рассмотрим 3 варианта.
1)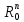 .
ρ(x,y)=
.
ρ(x,y)=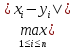 .
ρ(y1,y2)=
.
ρ(y1,y2)=
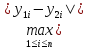 ≤
≤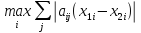 ≤
≤
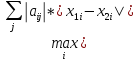 ≤
≤
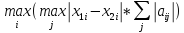 ≤
≤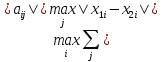 =
=
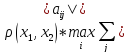 .
Отображение будет сжимающим, если
.
Отображение будет сжимающим, если
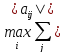 ≤α<1
(2). Т.о. нужно взять суммы модулей всех
коэффициентов, в каждой троке которых
наибольшая из этих сумм должна быть <
1 (критерий по строкам) .
≤α<1
(2). Т.о. нужно взять суммы модулей всех
коэффициентов, в каждой троке которых
наибольшая из этих сумм должна быть <
1 (критерий по строкам) .
