
- •2.1.1. Решение задания по статье.
- •1.3.1. Решение задачи по статье.
- •Результаты нарушений на различных стадиях мейоза у ели сибирской
- •1.1.1. Почему эколог должен стремится к «введению случайностей» в эксперимент?
- •1.1.2. С чем связана необходимость применения статистических методов в биологической науке?
УЕ 2.5
Задача 2.5.1 для задания 2.5.7

2.5.1
N=20
∑d2(x-y)2= 154.5
rs= 0.884
Сильная корреляционная связь так как rs˃ 0.70
+2
Задача 2.5.1 для задания 2.5.8
∑ xi= 1074
∑yi = 622
∑ xi2= 58602
∑ yi2= 20014
∑xiyi= 34226
r
= 1.045
sx = 1,60
sy= 1.36
Rx/y=
1.23
Ry/x=
8.88
+0
УЕ 2.4
Но-1 и 2 выборки отличаются
|
1 выборка |
Ранг (Т1) |
2 выборка |
Ранг (Т2) |
|
33 |
6.5 |
35 |
15 |
|
35 |
15 |
36 |
20 |
|
34 |
10.5 |
33 |
6.5 |
|
36 |
20 |
35 |
15 |
|
38 |
21 |
35 |
15 |
|
33 |
6.5 |
36 |
20 |
|
34 |
10.5 |
33 |
6.5 |
|
35 |
15 |
32 |
2.5 |
|
33 |
6.5 |
30 |
1 |
|
32 |
2.5 |
35 |
15 |
|
35 |
15 |
33 |
6.5 |
Т1 =129
Т2 =123
U=(11*11)+(11(11+1)/2)-129=58
Uкр=34(Р<0.05)
25(P<0.01)
Uэмп<Uкр,
Н0: принимается.
УЕ 2.4.2.
Ho: Пищевого предпочтения у видов Macrolepidoptera не существует
|
Трофические группы |
Эмпирическая частота (Fo) |
Теоретическая частота(Fe) |
Х2=(Fo-Fe)2/Fe |
|
1 |
272 |
123.5 |
178.56 |
|
2 |
277 |
123.5 |
190.79 |
|
3 |
63 |
123.5 |
29.64 |
|
4 |
71 |
123.5 |
22.32 |
|
5 |
14 |
123.5 |
97.09 |
|
6 |
44 |
123.5 |
51.18 |
|
Суммы |
741 |
741 |
569.58 |
X2= 569.58
X2krit= 11.07(P<0.05)
15.08(P<0.01)
X2>X2krit
Ответ: нулевая гипотеза отвергается
УЕ 2.4.3
Н0: отличий выживаемости дафний в сосудах нет
Х2эмп= 0.89
df=1
X2кр= 3.841(Р005)и 6.635 (Р001)
Х2эмп ˂ Х2кр
Н0: подтверждена
УЕ 2.4.4.
Ho: численность самцов благородного оленя на острове Рам на 15 участках не отличается от нормально распределения.
|
Участок |
Эмпирическая частота (Fo) |
Теоретическая частота(Fe) |
X^2=(Fo-Fe)^2/Fe |
|
1 |
107.0 |
46.9 |
77.02 |
|
2 |
74.9 |
46.9 |
16.72 |
|
3 |
79.4 |
46.9 |
22.52 |
|
4 |
70.1 |
46.9 |
11.48 |
|
5 |
85.9 |
46.9 |
32.43 |
|
6 |
78.4 |
46.9 |
21.16 |
|
7 |
79.2 |
46.9 |
22.24 |
|
8 |
59.1 |
46.9 |
3.17 |
|
9 |
29.5 |
46.9 |
6.46 |
|
10 |
11.3 |
46.9 |
27.02 |
|
11 |
9.3 |
46.9 |
30.14 |
|
12 |
8.7 |
46.9 |
31.11 |
|
13 |
3.5 |
46.9 |
40.16 |
|
14 |
5.7 |
46.9 |
36.19 |
|
15 |
1.5 |
46.9 |
43.95 |
|
Суммы |
703.5 |
703.5 |
421.77 |
X2=421.77
X2krit=23.689(P<0.05)
29.141(P<0.01)
X2>X2krit
H0: отклоняется
Задача 2.3.1 для задания 2.4.1
Н0: Нифедипин не влияет на артериальное давление у собак.
Т1=165.5 Т2=87.5
Uэмп=21.5
Uкр= 34(P005) и 22(P001)
Uэмп больше Uкр
Н0: опровергнута
+2
УЕ 2.4.6
Н0: Различий численности бабочек двух форм не существует
Т1=132 Т2=121
Uэмп=55
Uкр= 34(Р005) и 25(Р001)
Uэмп большеUкр
Н0: подтверждена
+2
УЕ 2.4.7
Н0: различий между двумя экологическими нишами ящериц не существует
Т1=131 Т2=122
Uэмп= 56
Uкр= 34(Р005) и 25(Р001)
Uэмп большеUкр
Н0: подтверждена
+2
Задание УЕ 2.3.
Задача 2.3.14. Решение:
|
Х1 |
(xi– x-) |
(xi– x-)2 |
X2 |
(x2 – x-) |
(x2 – x-)2 | |
|
8 |
|
2621,44 |
0 |
-7,4 |
54,76 | |
|
127 |
67,8 |
4596,84 |
15 |
7,6 |
57,76 | |
|
34 |
-25,2 |
635,04 |
5 |
-2,4 |
5,76 | |
|
23 |
-36,2 |
1310,44 |
3 |
-4,4 |
19,36 | |
|
55 |
-4,2 |
17,64 |
10 |
2,6 |
6,76 | |
|
37 |
-22,2 |
492,84 |
3 |
-4,4 |
19,36 | |
|
76 |
|
282,24 |
9 |
1,6 |
2,56 | |
|
75 |
|
249,64 |
13 |
5,6 |
31,36 | |
|
77 |
|
316,84 |
11 |
3,6 |
12,96 | |
|
66 |
|
46,24 |
9 |
1,6 |
2,56 | |
|
73 |
|
190,44 |
3 |
-4,4 |
19,36 | |
|
n = df = x- = |
11 10 52.9
|
10759,64 |
n = df = x- = |
11 10 7,4
|
232,56 |
S1
=
 =
=
 = 32,8
= 32,8
 =
=
 =
=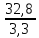 = 9,93
= 9,93
S2
=
 =
=
 = 4,82
= 4,82
 =
=
 =
= = 1,46
= 1,46
t
=
 =
= = 4,54
= 4,54
H0 – между двумя выборками бабочек Bistolbetularia по цветовой форме НЕ СУЩЕСТВУЕТ отличий.
Значения находятся в зоне значимости, значит нулевую гипотезу мы отвергаем = различия между двумя выборками бабочек Bistolbetularia по цветовой форме существует.
+0
УЕ 2.3.4.
1 выборка- №1
N=12
1) 1=13,6
1=13,6
2)D1:
ХD1=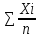 =
=
3)Сигма
D1 =1,32
=1,32
4)CVD1= =9,71
=9,71
2 выборка , см- №2
 2=13,3
2=13,3
S2=1,33
CV2=10
5) 1=0,381
1=0,381
 2= 0,384
2= 0,384
 1=0,269
1=0,269
 2=0,271
2=0,271
T=0,55
H0 : между двумя выборками нитратов, содержащихся в снеге, различий не существует.
0.05
0.01
0.55 2.20 2.72
P>0.05 P<0.05 P<0.01
F=0.98=1
Ответ: значение находится в зоне не значимости =нулевая гипотеза остается.
+2
УЕ 2.3.7.
Высота ,м- №1
Диаметр , см- №2
N=26
 1=29,58
1=29,58
 2=31,96
2=31,96
S1=3.09 S2=6.17
CV1=10.45 CV2=19.31
 1=0.61
1=0.61
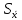 2= 1.21
2= 1.21
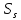 1=0.43
1=0.43
 2=0.86
2=0.86
T=1.76
H0 : Между высотой и диаметром лиственницы сибирской отличий нет.
0.05
0.01
1.76 2.06 2.49
P>0.05 P<0.05 P<0.01
Ответ: P>0.05 Между высотой и диаметром лиственницы сибирской различий нет.
+2
УЕ 2.3.9.
Выборка 1 - №1
Выборка 2 - №2
N=12
 1=19,7
1=19,7
 2=21,5
2=21,5
S1=3.28 S2=2,19
CV1=16,57 CV2=10,19
 1=0,95
1=0,95
 2= 0,63
2= 0,63
 1=0,67
1=0,67
 2=0,45
2=0,45
T=1,71
H0 : Между 1 выборкой и 2 выборкой отличий нет.
0.05
0.01
1.71 2,20 2,72
P>0.05 P<0.05 P<0.01
Ответ: Различия между районами по количеству рожденных клещей нет.
+2
Задача 2.3.5. Решение:
|
Х1 |
(xi – x-) |
(xi – x-)2 |
X2 |
(x2 – x-) |
(x2 – x-)2 |
|
3 |
-0,3 |
0,09 |
1 |
-3,6 |
12,96 |
|
5 |
1,7 |
2,89 |
5 |
0,4 |
0,16 |
|
4 |
0,7 |
0,49 |
3 |
-1,6 |
2,56 |
|
3 |
-0,3 |
0,09 |
7 |
2,4 |
5,76 |
|
3 |
-0,3 |
0,09 |
7 |
2,4 |
5,76 |
|
1 |
-2,3 |
5,29 |
5 |
0,4 |
0,16 |
|
6 |
2,7 |
7,29 |
3 |
-1,6 |
2,56 |
|
2 |
-1,3 |
1,69 |
5 |
0,4 |
0,16 |
|
3 |
-0,3 |
0,09 |
4 |
-0,6 |
0,36 |
|
2 |
-1,3 |
1,69 |
2 |
-2,6 |
6,76 |
|
5 |
1,7 |
2,89 |
6 |
1,4 |
1,96 |
|
3 |
-0,3 |
0,09 |
7 |
2,4 |
5,76 |
|
n = df = x- = |
12 11 3,3
|
22,68 |
n = df = x- = |
12 11 4,6
|
44,92 |
S1
=
 =
=
 =
1,43
=
1,43
 =
=
 =
= =
0,41
=
0,41
S2
=
 =
=
 =
4,08
=
4,08
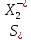 =
=
 =
= = 1,17
= 1,17
t
=
 =
= = 1,08
= 1,08
H0 – между двумя сообществами по видовому составу жесткокрылых НЕ СУЩЕСТВУЕТ различий.
Значения находятся в зоне значимости, значит нулевую гипотезу мы отвергаем = различия между двумясообществами по видовому составу жесткокрылых существует.
F – критерия
F
=
 =
=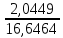 = 0,123
= 0,123
+0
Задание УЕ 2.2.
Задание 2.2.2. (задача 2.1.5 для задания 2.2.2.)
Всего вариантов (объем совокупностей, N) = 30
R = xmax – xmin = 56 – 40 = 16
Невозможно провести группировку по количеству, т.к. 16 классов для данного объема совокупностей много.
Количество
классов K
=
 =
= = 5,5(округляем) = можно выбрать как 5, так
и 6.
= 5,5(округляем) = можно выбрать как 5, так
и 6.
Определяем
классовый интервал: L
=
 =
=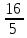 =3,2
поскольку вариация прерывистая выбираем
классовый интервал как дробное округленное
число =3.
=3,2
поскольку вариация прерывистая выбираем
классовый интервал как дробное округленное
число =3.
Определение начала и конца каждого группового интервала:
Начало Конец
1 класс = 40 42
2 класс = 40 + 3 =43 45
3 класс = 40 + 2*3 = 46 48
4 класс = 40 + 3*3= 49 51
5 класс = 40 + 4*3 = 52 54
6 класс = 40 + 5*3 = 55 56
составляем вариационный ряд
|
Значение классов |
40-42 |
42-45 |
46-48 |
49-51 |
52-54 |
55-56 |
|
|
|
|
|
|
|
|
|
Частота |
1
|
- |
2 |
6 |
14 |
7 |
X = 52,3
+
3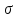 =
62,2
=
62,2
-3 = 42,4
= 42,4

Выборки по данной задаче извлечены из совокупности с нормальным распределением, т.к. данные выборки соответствуют с кривой распределения.
Задание 2.2.3. (задача 2.1.6 для задания 2.2.3)
Ошибка среднего отклонения
Sx-
=

Sx-
= =
= =0.21
=0.21
Ошибка стандартного отклонения
 =
=
 =
=
 =
= 0.15
0.15
Задание 2.2.1
Способов не существует, так как имеются пробелы
Средняя ошибка для выборки 1
=0,29/3,16=0,09
Ошибка стандартного отклонения для выборки 1
=0,29/4,47=0.064
Средняя ошибка для выборки 2
=)0,25/3,16=0,08
Ошибка стандартного отклонения для выборки2
=0,25/4,47=0,055
Задание УЕ 2.1.
2.1.1. Решение задания по статье.
среднее арифметическое отдельной выборки D1(см. задание 1.3.1 таблица)
 =
=
x-=
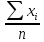 =
=
 =0,665
(округлим) = 0,67
=0,665
(округлим) = 0,67
2.1.модальный классв выборке : г.Златоуст.
мода (Мо) в выборке: 0.60
2.2.стандартное отклонение в выборке:
|
№ |
|
|
| ||
|
|
( |
( | |||
|
1 |
0.40 |
-0,27 |
0,0729 | ||
|
2 |
1.30 |
0,63 |
0,3969 | ||
|
3 |
0.20 |
-0,47 |
0,2209 | ||
|
4 |
0.60 |
-0,07 |
0,0049 | ||
|
5 |
0.20 |
-0,47 |
0,2209 | ||
|
6 |
0.14 |
-0,53 |
0,2809 | ||
|
7 |
0.36 |
-0,31 |
0,0961 | ||
|
8 |
0.24 |
-0,43 |
0,1849 | ||
|
9 |
0.51 |
0,16 |
0,0256 | ||
|
10 |
2.70 |
2,03 |
4,1209 | ||
|
|
0,67 |
| |||
|
df = (n-1) |
9 |
|
5,6249 | ||
S
=
 =
= =
0,79
=
0,79
2.3.коэффициент вариации (CV) в выборке:
CV
=
 =
=
 =
118,0
=
118,0
2.1.3
1)D1:
ХD1=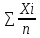 =
= =13,62667
=13,62667
2)Сигма
D1 =
= =
1,249257
=
1,249257
3)CVD1= =
=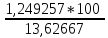 =
9,167740068
=
9,167740068
Задача 2.1.5. было подсчитано число щетинок на сторонах тела мухи Drosophilamelanogaster:
|
53 |
51 |
52 |
55 |
56 |
55 |
53 |
47 |
56 |
49 |
|
54 |
53 |
52 |
53 |
51 |
48 |
56 |
52 |
51 |
55 |
|
51 |
51 |
56 |
54 |
54 |
40 |
52 |
53 |
54 |
53 |
среднее арифметическое отдельной выборки
 =
=
х-
=
 =
=
 =52,3
=52,3
модальный класс в выборке :
мода (Мо) в выборке : 56
стандартное отклонение в выборке:
|
№ |
|
|
| |||
|
|
( |
( | ||||
|
1 |
53 |
|
0,49 | |||
|
2 |
51 |
-1,3 |
1,69 | |||
|
3 |
52 |
-0,3 |
0,09 | |||
|
4 |
55 |
2,7 |
7,29 | |||
|
5 |
56 |
3,7 |
13,69 | |||
|
6 |
55 |
2,7 |
7,29 | |||
|
7 |
53 |
0,7 |
0,49 | |||
|
8 |
47 |
-5,3 |
28,09 | |||
|
9 |
56 |
3,7 |
13,69 | |||
|
10 |
49 |
-3,3 |
10,89 | |||
|
11 |
54 |
1,7 |
2,89 | |||
|
12 |
53 |
0,7 |
0,49 | |||
|
13 |
52 |
-0,3 |
0,09 | |||
|
14 |
53 |
0,7 |
0,49 | |||
|
15 |
51 |
-1,3 |
1,69 | |||
|
16 |
48 |
-4,3 |
18,49 | |||
|
17 |
56 |
3,7 |
13,69 | |||
|
18 |
52 |
-0,3 |
0,09 | |||
|
19 |
51 |
-1,3 |
1,69 | |||
|
20 |
55 |
2,7 |
7,29 | |||
|
21 |
51 |
-1,3 |
1,69 | |||
|
22 |
51 |
-1,3 |
1,69 | |||
|
23 |
56 |
3,7 |
13,69 | |||
|
24 |
54 |
1,7 |
2,89 | |||
|
25 |
54 |
1,7 |
2,89 | |||
|
26 |
40 |
-12,3 |
151,29 | |||
|
27 |
52 |
-0,3 |
0,09 | |||
|
28 |
53 |
0,7 |
0,49 | |||
|
29 |
54 |
1,7 |
2,89 | |||
|
30 |
53 |
0,7 |
0,49 | |||
|
|
52,3 |
| ||||
|
df = (n-1) |
29 |
|
308,7 | |||
S
=
 =
= = 3,3
= 3,3
коэффициент вариации (CV) в выборке :
CV
=
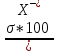 =
=
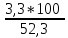 =6,31.
=6,31.
Задача 2.1.6. обхват тела у карпа в возрасте полгода (см):
|
14,3 |
15,7 |
14,8 |
15,3 |
15,0 |
14,5 |
12,9 |
14,4 |
14,4 |
14,2 |
|
14,3 |
12,0 |
14,4 |
13,0 |
13,8 |
13,5 |
12,5 |
13,5 |
13,5 |
12,4 |
|
12,8 |
11,9 |
12,0 |
13,8 |
13,0 |
14,3 |
14,5 |
12,3 |
12,3 |
11,4 |
среднее арифметическое отдельной выборки:
 =
=
 =
=
 =
=
 =13,6
=13,6
модальный класс в выборке:
мода (Мо) в выборке: 15,7.
стандартное отклонение в выборке D1:
|
№ |
|
|
| ||
|
|
( |
( | |||
|
1 |
14,3 |
0,7 |
0,49 | ||
|
2 |
15,7 |
2,1 |
4,41 | ||
|
3 |
14,8 |
1,2 |
1,44 | ||
|
4 |
15,3 |
1,7 |
1,89 | ||
|
5 |
15,0 |
1,4 |
1,96 | ||
|
6 |
14,5 |
0,9 |
0,81 | ||
|
7 |
12,9 |
-0,7 |
0,49 | ||
|
8 |
14,4 |
0,8 |
0,64 | ||
|
9 |
14,4 |
0,8 |
0,64 | ||
|
10 |
14,2 |
0,6 |
0,36 | ||
|
11 |
14,3 |
0,7 |
0,49 | ||
|
12 |
12,0 |
-1,6 |
2,56 | ||
|
13 |
14,4 |
0,8 |
0,64 | ||
|
14 |
13,0 |
-0,6 |
0,36 | ||
|
15 |
13,8 |
0,2 |
0,04 | ||
|
16 |
13,5 |
-0,1 |
0,01 | ||
|
17 |
12,5 |
-1,1 |
1,21 | ||
|
18 |
13,5 |
-0,1 |
0,01 | ||
|
19 |
13,5 |
-0,1 |
0,01 | ||
|
20 |
12,4 |
-1,2 |
1,44 | ||
|
21 |
12,8 |
-0,8 |
0,64 | ||
|
22 |
11,9 |
-1,7 |
2,89 | ||
|
23 |
12,0 |
-1,6 |
2,56 | ||
|
24 |
13,8 |
0,2 |
0,04 | ||
|
25 |
13,0 |
-0,6 |
0,36 | ||
|
26 |
14,3 |
0,7 |
0,49 | ||
|
27 |
14,5 |
0,9 |
0,81 | ||
|
28 |
12,3 |
-1,3 |
1,69 | ||
|
29 |
12,3 |
-1,3 |
1,69 | ||
|
30 |
11,4 |
-2,2 |
4,84 | ||
|
|
13,6 |
| |||
|
df = (n-1) |
29 |
|
36,91 | ||
S
=
 =
= = 1,13
= 1,13
коэффициент вариации (CV) в выборке:
CVD1
=
 =
=
 =8,3.
=8,3.
УЕ 1.3

 =
=
 =
= =
=
 =
=
 -
-
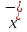 )
) -
-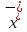 )2
)2


 -
- )
) -
- )2
)2
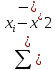

 -
- )
) -
-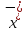 )2
)2
