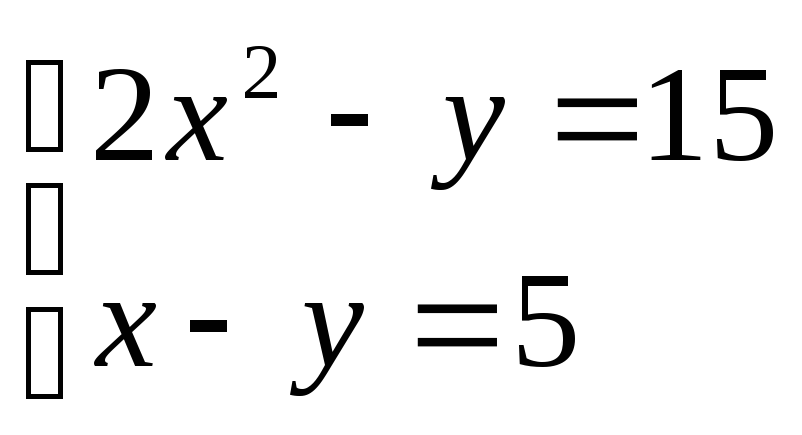Приближенное решение определенных интегралов

При решении технических задач приходится находить определенные интегралы от функций, первообразные которых не выражаются через элементарные функции. Для этого существуют формулы приближенного вычисления: формула прямоугольников, формула трапеций и формула парабол (Симпсона).

Геометрический смысл определенного интеграла ­ площадь криволинейной трапеции, ограниченной осью ОХ, кривой и прямыми х=а х=b. Разобъем отрезок точками х₀, х₁,…х_n на n элементарных отрезков. Получим n криволинейных фигур.

Формула прямоугольников

• где

. Чем больше число n, тем меньше погрешность расчетов.

Суть метода прямоугольников в том, что на каждом из участков разбиения [x_i-1, x_i] участок кривой заменяется отрезком прямой, параллельным оси абсцисс. Тогда определенный интеграл приближенно равен сумме площадей прямоугольников на каждом участке разбиения.

Пример. Вычислить определенный интеграл , используя формулу прямоугольников.

=C7*$D$2+D6

=ЕСЛИ(B7>=$B$2;D7-$D$2*$B$4;"...")

=ЕСЛИ(A7<=$C$2;B6+$D$2;"стоп")

Ответ

Формула трапеций.

• , где

. Чем больше число n, тем меньше погрешность расчетов.

Метод трапеций является более точным, т.к. каждый участок кривой заменяется не прямыми, а хордами, стягивающими концевые точки. Тогда каждое слагаемой интегральной суммы будет равно площади трапеции с основаниями f(x_i) и f(x_i-1) и высотой h.

Пример. Вычислить определенный интеграл , используя формулу трапеций.

=D2*((C6+C16)/2+СУММ(C7:C15))

Ответ

Формула Симпсона (парабол)

В основе формулы Симпсона лежит интерполяция подынтегральной функции многочленом второй степени, т.е. подынтегральная функция на каждом элементарном отрезке заменяется параболой, построенной по трем точкам ­ ,,.Тогда значение интеграла можно приближенно получить по формуле

, где

.

Пример. Вычислить определенный интеграл , используя формулу Симпсона.

В ячейку N2 введена формула, которая не позволит ввести нечетное n.

=ЕСЛИ(ОСТАТ(K7;2);N6+M7*4;N6+M7*2)

=ЕСЛИ(L10>=$L$2;(N10-$L$4)*$N$2/3;"...")

=ЕСЛИ(ОСТАТ(M2;2)=0;(L2-K2)/M2;"нечетное п не допускается")

Ответ

Задания для самостоятельного выполнения.

Внимание! Решенным считается задание, в котором получен правильный ответ, и который можно переделать путем введения новых исходных данных (все остальное пересчитывается автоматически).

Задание 1. Построить график функции в Excel.

Вариант		Интервал
		[-5, 5]х=0,5
		[-5, 5]х=0,5
		[-5, 3]х=0,5
		[0, 5]х=0,5
		[0,5; 5]х=0,5
		[0, 10]х=0,5
		[0,1; 2]х=0,1
		[0, 10]х=0,5
		[1, 5] х=0,2

Задание 2. Решить систему уравнений в Excel

Вариант		Интервал
1		[-5, 5]х=1
2		[1, 10]х=1
3		[-5, 5]х=0,5
4		[-2, 2]х=0,2
5		[0,5; 4,5]х=0,2
6		[-5, 5]х=0,5
7	Решить уравнение	[-2, 2]х=0,2
8	Решить уравнение	[0; 4]х=0,2
9		[0, 5]х=0,5

Задание 3. Аппроксимация экспериментальных данных методом наименьших квадратов

Вариант
	хi 0,75 1,5 2,25 3 3,75 yi 2,5 1,2 1,12 2,25 4,28
	хi 2,5 8,3 14,10 20,5 26,1 yi 0,17 0,13 0,1 0,13 0,22
	хi 0,12 0,13 0,14 0,16 0,19 yi 8,65 8,29 7,95 7,64 7,36
	хi 0,15 0,2 0,25 0,3 0,35 yi 6,61 6,39 6,19 6 5,82
	хi 0,18 0,19 0,20 0,22 0,24 yi 5,61 5,46 5,32 5,19 5,06
	хi 0,4 0,47 0,51 0,6 0,67 yi 0,21 0,19 0,18 0,16 0,15
	хi 5,1 11,9 17,50 23,1 29,4 yi 0,93 0,79 0,71 0,75 0,91
	хi -1 0 1,00 2 3 yi 1,5 0,01 0,9 3,8 9,35
	хi 6 6,4 6,80 7,2 7,6 yi 1,2 2,45 4,4 7,2 15,00