Лабораторная работа № 10 определение коэффициента теплопроводности металла

Цель работы: определение коэффициента теплопроводности металла и распределения температуры вдоль металлического стержня, нагреваемого с одного конца.

Оборудование: экспериментальная установка, секундомер.

1. Краткая теория и методика выполнения работы

Перенос тепла (энергии в форме теплоты ) в твердых телах и газах описывается законом Фурье:

, (10.1)

где – плотность теплового потока вдоль оси,– коэффициент теплопроводности,– градиент температуры, характеризующий быстроту ее убывания при удалении от источника тепла. Знак «минус» означает, что перенос энергии через поперечное сечение площадьюпроисходит в сторону меньших температур.

Коэффициент теплопроводности металлов , и достигает максимального значения у серебра, что значительно превышает коэффициент теплопроводности газов.

Процесс теплопроводности в твердых телах осуществляется путем взаимодействия колеблющихся в узлах кристаллической решетки ионов и валентных электронов атомов, которые являются обобществленными, могут перемещаться от атома к атому и рассматриваться как электронный газ. Наиболее интенсивное колебание частиц, существующее в области повышенной температуры, передается соседним частицам, постепенно распространяясь на все тело.

Кроме того, теплопроводность в металлах значительно увеличивается благодаря наличию свободных электронов, которые могут перемещаться внутри металла, непосредственно перенося свою кинетическую энергию из области повышенной температуры в область более низкой. Важная роль свободных электронов в процессе теплопроводности подтверждается тем фактом, что теплопроводность металлов приблизительно пропорциональна их электропроводности.

Представим себе бесконечно длинный металлический стержень, один конец которого находится в печи (рис. 10.1, а).

Электроны и ионы, находящиеся в слое металла с координатойвблизи печи, получают от неё дополнительную кинетическую энергию и передают её электронам и ионам соседнего слоя с координатой. Стержень, получая тепло от печи, будет нагреваться. Одновременно с его поверхности часть тепла уносится воздушным потоком (конвекция). С течением времени устанавливается стационарное состояние, при котором распределение температуры вдоль стержня не меняется и имеет вид, показанный на рис. 10.1, б.

Найдем уравнение теплопроводности, описывающее распределение температуры вдоль стержня.

Согласно (10.1) количества тепла, ежесекундно проходящие через сечение стержня в точкахи, равны соответственно:

(10.2)

Количество тепла, отдаваемое с поверхности отрезком стержня между этими координатами, прямо пропорционально разности температур:

(10.3)

где – коэффициент теплоотдачи металла,– периметр поперечного сечения стержня,и– температуры элемента стержня и воздуха соответственно.

В условиях стационарного режима количество тепла, передаваемого стержню, равно количеству тепла, отдаваемого им в окружающую среду, т.е. или в соответствии с (10.2) и (10.3):

. (10.4)

Учитывая, что:

,

получим из выражения (10.4) дифференциальное уравнение второго порядка:

, (10.5)

здесь:

. (10.6)

Уравнение типа (10.5) имеет стандартное решение вида:

, (10.7)

где и– произвольные постоянные.

По мере удаления от печи () температура стержня убывает, приближаясь к комнатной (). Тогда уравнение (10.7) выполняется, если. Для начальной точки отсчета,. Тогда из (10.7). С учетом полученных значенийиуравнение (10.7) примет вид:

. (10.8)

После логарифмирования получим выражение:

. (10.9)

Рассчитаем тепло, теряемое бесконечно длинным отрезком стержня ежесекундно. Используя (10.3) и (10.8), запишем:

и после интегрирования получим:

.

Согласно (10.6) , тогда, откуда:

.

Подставив из (10.9) значение , получаем формулу для расчета коэффициента теплопроводности металла:

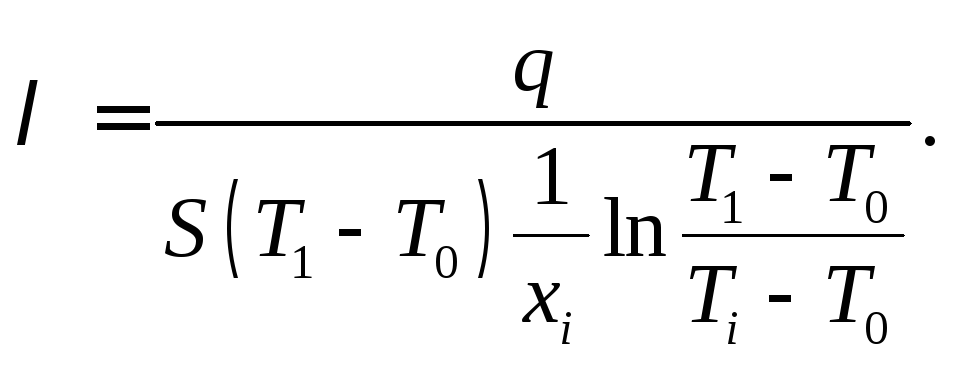(10.10)

В формулу (10.10) входит разность абсолютных температур (по шкале Кельвина). Однако она равна разности температур по шкале Цельсия, т.е. .

Количество тепла, ежесекундно отдаваемое электропечью, вычисляется по формуле:

. (10.11)

Здесь– мощность печи,– её к.п.д. (коэффициент полезного действия) при теплоотдаче.