
- •Лабораторная работа № 4 определение отношения изобарной и изохорной теплоёмкостей газа
- •1. Краткая теория и методика выполнения работы
- •2. Описание экспериментальной установки
- •3. Выполнение упражнений и обработка результатов измерений
- •4. Контрольные вопросы
- •Лабораторная работа № 5 определение коэффициента диффузии паров воды в воздухе
- •1. Краткая теория и методика выполнения работы
- •2. Описание экспериментальной установки
- •3. Выполнение упражнений и обработка результатов измерений
- •4. Контрольные вопросы
- •Лабораторная работа № 6 определение молярной теплоты парообразования воды
- •1. Краткая теория
- •2. Описание экспериментальной установки
- •3. Выполнение упражнений и обработка результатов измерений
- •4. Контрольные вопросы
Лабораторная работа № 4 определение отношения изобарной и изохорной теплоёмкостей газа
Цель работы: измерение отношения изобарной и изохорной теплоемкостей воздуха.
Оборудование: экспериментальная установка ФПТ1-6н.
1. Краткая теория и методика выполнения работы
Удельной теплоемкостью вещества называется величина, равная количеству теплоты, которую необходимо сообщить единице массы вещества для увеличения ее температуры на один градус Кельвина:
![]() . (4.1)
. (4.1)
Теплоемкость одного моля вещества называется молярной теплоемкостью:
 , (4.2)
, (4.2)
где
m – масса, µ – молярная масса вещества,
![]() – число молей газа.
– число молей газа.
Значение
теплоемкости газов зависит от условий
их нагревания. В соответствии с первым
законом термодинамики количество
теплоты
![]() ,
сообщенное системе, расходуется на
увеличение ее внутренней энергии
,
сообщенное системе, расходуется на
увеличение ее внутренней энергии![]() и на совершение системой работы
и на совершение системой работы![]() против внешних сил:
против внешних сил:
![]() . (4.3)
. (4.3)
Изменение
внутренней энергии идеального газа в
случае изменения его температуры
![]() равно:
равно:
![]() , (4.4)
, (4.4)
здесь
![]() – число степеней свободы молекулы газа,
под которым подразумевается число
независимых координат, полностью
определяющих положение молекулы в
пространстве;
– число степеней свободы молекулы газа,
под которым подразумевается число
независимых координат, полностью
определяющих положение молекулы в
пространстве;![]() – универсальная газовая постоянная.
– универсальная газовая постоянная.
При расширении газа система совершает работу:
![]() . (4.5)
. (4.5)
Если
газ нагревать при постоянном объеме
(![]() ),
то
),
то![]() и, согласно (4.3), все полученное газом
количество теплоты расходуется только
на увеличение его внутренней энергии
и, согласно (4.3), все полученное газом
количество теплоты расходуется только
на увеличение его внутренней энергии![]() .
Следовательно, учитывая (4.4), молярная
теплоемкость идеального газа при
постоянном объеме будет равна:
.
Следовательно, учитывая (4.4), молярная
теплоемкость идеального газа при
постоянном объеме будет равна:
![]() . (4.6)
. (4.6)
Если
газ нагревать при постоянном давление
(![]() ),
то полученное газом количество теплоты
расходуется на увеличение его внутренней
энергии
),
то полученное газом количество теплоты
расходуется на увеличение его внутренней
энергии![]() и совершение газом работы
и совершение газом работы![]() :
:
![]() .
.
Тогда молярная теплоемкость идеального газа при постоянном давлении определяется следующим образом:
![]() . (4.7)
. (4.7)
Используя
уравнение состояния идеального газа
(уравнение Клапейрона–Менделеева)
![]() ,
можно показать, что для одного моля газа
справедливо соотношение:
,
можно показать, что для одного моля газа
справедливо соотношение:
![]() ,
,
поэтому:
![]() .
.
Последнее выражение называют уравнением Майера. Из него, учитывая (4.6), получаем:
![]() . (4.8)
. (4.8)
Отношение
теплоемкостей
![]() обозначают
обозначают![]() и называют показателем адиабаты или
коэффициентом Пуассона:
и называют показателем адиабаты или
коэффициентом Пуассона:
![]() . (4.9)
. (4.9)
Адиабатным
называется процесс, протекающий в
термоизолированной системе, т.е. без
теплообмена с окружающей средой,
![]() .
.
На практике он может быть осуществлен в системе, окруженной теплоизоляционной оболочкой, но поскольку для теплообмена необходимо некоторое время, то адиабатным можно считать также процесс, который протекает так быстро, что система не успевает вступить в теплообмен с окружающей средой.
Первый
закон термодинамики для адиабатного
процесса имеет вид
![]() .
Знак минус говорит о том, что при
адиабатном процессе система может
совершать работу только за счет внутренней
энергии. С учетом (4.4)–(4.6) имеем:
.
Знак минус говорит о том, что при
адиабатном процессе система может
совершать работу только за счет внутренней
энергии. С учетом (4.4)–(4.6) имеем:
![]() . (4.10)
. (4.10)
Продифференцировав уравнение Клапейрона–Менделеева, получим:
![]() .
.
Выразим
из него
![]() и подставим в формулу (4.10):
и подставим в формулу (4.10):
![]() .
.
Выразив
![]() из уравнения Майера и учитывая соотношение
(4.8), получим:
из уравнения Майера и учитывая соотношение
(4.8), получим:
![]() .
.
И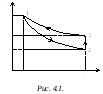 нтегрируя
данное дифференциальное уравнение при
условии
нтегрируя
данное дифференциальное уравнение при
условии![]() получим выражение:
получим выражение:
![]() .
(4.11)
.
(4.11)
Уравнение (4.11) называется уравнением адиабаты или уравнением Пуассона.
Метод
определения показателя адиабаты,
предложенный Клеманом и Дезормом (1819
г.), основывается на изучении параметров
некоторой массы газа, переходящей из
одного состояния в другое двумя
последовательными процессами –
адиабатным и изохорным. Эти процессы
на диаграмме
![]() –
–![]() (рис. 4.1) изображены кривыми соответственно
1–2 и 2–3.
(рис. 4.1) изображены кривыми соответственно
1–2 и 2–3.
Если
в сосуд, соединенный с дифференциальным
датчиком давления, накачать воздух и
подождать до установления теплового
равновесия с окружающей средой, то в
этом начальном состоянии 1 газ имеет
параметры
![]() ,
,![]() ,
,![]() ,
причем температура газа в сосуде равна
температуре окружающей среды
,
причем температура газа в сосуде равна
температуре окружающей среды![]() ,
а давление
,
а давление![]() немного больше атмосферного.
немного больше атмосферного.
Если
теперь на короткое время соединить
сосуд с атмосферой, то произойдет
адиабатное расширение воздуха. При этом
воздух в сосуде перейдет в состояние
2, его давление понизится до атмосферного
![]() .
Масса воздуха, оставшегося в сосуде,
которая в состоянии 1 занимала часть
объема сосуда, расширяясь, займет весь
объем
.
Масса воздуха, оставшегося в сосуде,
которая в состоянии 1 занимала часть
объема сосуда, расширяясь, займет весь
объем![]() .
При этом температура воздуха, оставшегося
в сосуде, понизится до
.
При этом температура воздуха, оставшегося
в сосуде, понизится до![]() .
Поскольку процесс 1–2 – адиабатный, к
нему можно применить уравнение Пуассона
(4.11):
.
Поскольку процесс 1–2 – адиабатный, к
нему можно применить уравнение Пуассона
(4.11):
![]() или
или
![]() .
.
Отсюда:
![]() . (4.12)
. (4.12)
После
кратковременного соединения сосуда с
атмосферой охлажденный из-за адиабатного
расширения воздух в сосуде будет
нагреваться (процесс 2–3) до температуры
окружающей среды
![]() при постоянном объеме
при постоянном объеме![]() .
При этом давление в сосуде поднимется
до
.
При этом давление в сосуде поднимется
до![]() .
.
Поскольку процесс 2–3 – изохорный, к нему можно применить закон Шарля:
![]() или
или
![]() . (4.13)
. (4.13)
Из уравнений (4.12) и (4.13) получим:
![]() .
.
Прологарифмируем это выражение:
![]() .
.
Поскольку
избыточные давления
![]() и
и![]() очень малы по сравнению с атмосферным
давлением
очень малы по сравнению с атмосферным
давлением![]() ,
а также учитывая, что при
,
а также учитывая, что при![]()
![]() ,
будем иметь:
,
будем иметь:
![]() .
.
Откуда:
![]() . (4.14)
. (4.14)
Избыточные
давления
![]() и
и![]() измеряют с помощью дифференциального
датчика давления.
измеряют с помощью дифференциального
датчика давления.
