1.2. Оценка погрешностей косвенных измерений

Прежде чем рассматривать погрешности результата косвенных измерений, отметим, что погрешности, подсчи­танные по рекомендациям, изложенным в данном парагра­фе, носят ориентировочный характер. Мы остановимся на упрощенной трактовке.

Пусть искомая величина f определяется из прямых измерений величины x, причем: .

Обозначим искомое значение результата косвенных из­мерений через:

, (2.12)

где , а– абсолютная погрешность косвенного измерения величиныf.

Разложим функцию f в ряд Тейлора в окрестности точки :

, (2.13)

где – полная абсолютная погрешность прямо измеренной величиныx.

Начиная с третьего все члены ряда достаточно малы, и их можно отбросить. Тогда получим:

. (2.14)

Откуда:

. (2.15)

А так как , то

. (2.16)

Относительной погрешностью косвенного измерения называется величина равная:

, (2.17)

выраженная в долях единицы, или

, (2.18)

выраженная в процентах.

Часто бывает удобнее сначала вычислить относительную погрешность косвенного измерения, а затем определить абсолютную.

Раскроем в определении относительной погрешности косвенного измерения значение его абсолютной погрешности:

. (2.19)

В (2.19) внесем под знак дифференциала. Получим:

. (2.20)

Теперь, зная и, можно рассчитатькак:

. (2.21)

При расчете относительную погрешность следует брать выраженной в долях от единицы, а не в процентах.

Окончательный результат принято записывать в виде:

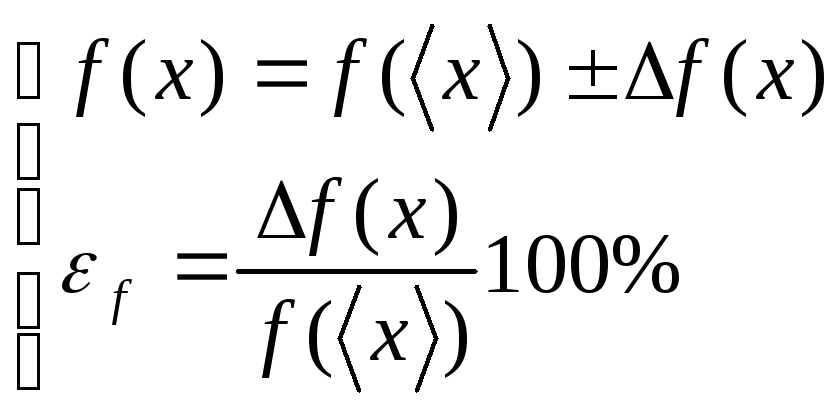. (2.22)

Рассмотрим теперь случай, когда искомая величина является функцией нескольких переменных, значения ко­торых определяются непосредственно из серий из­мерений: .

Так как каждая из прямо измеренных величин определена с некоторой ошибкой ,,и т.д., то каждая из них вносит свой вклад в абсолютную погрешность вычисляемой величиныf. Погрешности разных величин не могут компенсировать друг друга, каждая из них увеличивает неточность измеряемой величины, их следует складывать.

Проведя рассуждения, аналогичные вышеизложенным, для функции нескольких переменных получим, что абсолютную погрешность можно рассчитать по формуле:

, (2.23)

а относительную по формуле:

. (2.24)

Знаки обозначают частные производные (см. приложение 3).

Окончательный результат записывают в виде:

. (2.25)

Примеры расчета частных производных приведены в приложении 3.

1.3. Правила обработки результатов измерений

Указанные правила можно применять для случаев нормального распределения результатов или мало отличающихся от него.

Все расчеты ведутся с одной запасной цифрой, и только окончательный результат округляется!

Для прямых измерений

1. Результаты каждого измерения записывают в таблицу.

2. Вычисляют среднее арифметическое значение измеряемой величины: .

3. Находят абсолютные погрешности отдельных измерений: .

4. Вычисляют квадраты погрешностей отдельных измерений .

5. Задают значение надежности (доверительной вероятности) α. Определяют коэффициент Стьюдента t_,n для за­данной надежности α и числа произведенных измерений n (см. приложение 7).

6. Определяют случайную абсолютную погрешность серии измерений: .

7. Определяют абсолютную погрешность измерительного прибора: .

8. Вычисляют полную абсолютную погрешность серии измерений величины x: .

9. Находят границы доверительного интервала. Если величина погрешности результата измере­ний окажется сравнимой с величи­ной погрешности прибора, то в качестве границы довери­тельного интервала следует взять величину погрешности прибора.

10. Оценивают относительную погрешность резуль­тата серии измерений: .

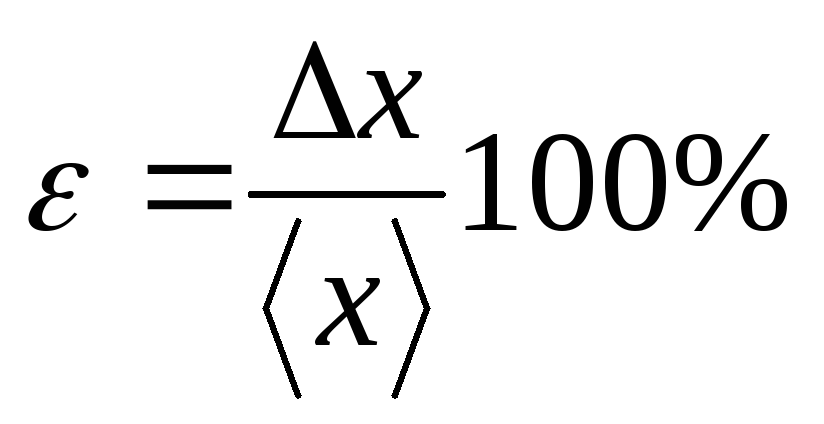11. Окончательный результат записывают в виде:

.